You are given the first n (or n + 1 if necessary) terms of a former power series P(x) = c0 + c1x + c2x2 + .... What operations can be performed efficiently?
Obviously, P(x) + Q(x), P(x) - Q(x), P'(x),
 , kP(x) for a given constant k, can be done in O(n).
, kP(x) for a given constant k, can be done in O(n).P(x)Q(x) can be done in O(nlogn) by FFT.
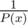 can be done in O(nlogn): Link, check problem E
can be done in O(nlogn): Link, check problem E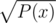 can be done in O(nlogn): Link, check problem E
can be done in O(nlogn): Link, check problem Eexp(P(x)) can be done in O(nlogn): Link, check Figure 1, left
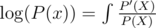 : Link
: LinkOpen: Can we do more complicated operations like P(Q(x)), P(x)1 / k, sin(P(x)), arcsin(P(x)), etc.? Are there other important operations?
Probably a bit related to the computation of
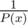 : when we are given two big decimal number x and y, can we compute x / y?
: when we are given two big decimal number x and y, can we compute x / y?






