How do we check if the round is rated for sure?

The round is rated for sure if anyone's rating has changed, that is, if a_i ≠ b_i for some i.

How do we check if the round is unrated for sure?

Given that all a_i = b_i, the round is unrated for sure if for some i < j we have a_i < a_j. This can be checked using two nested for-loops over i and j.

Exercise: can you check the same using one for-loop?

How do we find that it's impossible to determine if the round is rated or not?

If none of the conditions from steps 1 and 2 is satisfied, the answer is "maybe".

n = int(input())
results = []
for i in range(n):
    results.append(list(map(int, input().split())))

for r in results:
    if r[0] != r[1]:
        print("rated")
        exit()

for i in range(n):
    for j in range(i):
        if results[i][0] > results[j][0]:
            print("unrated")
            exit()

print("maybe")

Initially, we have x points. To win the current round, we need to score any number of points s such that s ≥ y.

If we know our final score s, we can check if we get the T-shirt using the given pseudocode. Moreover, since hacks change our score only by multiples of 50, the difference s - x has to be divisible by 50.

Naturally, out of all s satisfying the conditions above, we need to aim at the smallest possible s, since it's easy to decrease our score, but difficult to increase.

How many successful hacks do we need to make our score equal to s?

If s ≤ x, we need 0 successful hacks, since we can just make (x - s) / 50 unsuccessful hacks.

If s > x and s - x is divisible by 100, we need exactly (s - x) / 100 successful hacks.

If s > x and s - x is not divisible by 100, we need (s - x + 50) / 100 successful hacks and one unsuccessful hack.

All these cases can be described by a single formula for the number of successful hacks: (max(0, s - x) + 50) / 100 (here " / " denotes integer division).

#include <bits/stdc++.h>

using namespace std;

int main() {
  int p, x, y;
  cin >> p >> x >> y;
  for (int s = y; ; s++) {
    if (s % 50 != x % 50) {
      continue;
    }
    bool me = false;
    int i = s / 50 % 475;
    for (int j = 0; j < 25; j++) {
      i = (i * 96 + 42) % 475;
      if (i + 26 == p) {
        me = true;
        break;
      }
    }
    if (me) {
      printf("%d\n", (max(0, s - x) + 50) / 100);
      break;
    }
  }
  return 0;
}

The constraints were low enough, and the number of required hacks was also low enough. A less effective but easier solution can be achieved if we just iterate over both the number of successful and unsuccessful hacks we make. Once we know these two numbers, we know our final score s and we can explicitly check if this score gives us both the victory and the T-shirt.

p, x, y = map(int, input().split())

def check(s):
    i = (s // 50) % 475
    for t in range(25):
        i = (i * 96 + 42) % 475
        if 26 + i == p:
            return True
    return False

for up in range(500):
    for down in range(500):
        if x + 100 * up - 50 * down >= y and check(x + 100 * up - 50 * down):
            print(up)
            exit()

assert(False)

If our success rate is p / q, it means we have pt successful submissions out of qt for some t. Since p / q is already irreducible, t has to be a positive integer.

Let's reformulate things a bit. Initially we have x successful submissions and y - x unsuccessful ones. Suppose we fix t, and in the end we want to have pt successful submissions and qt - pt unsuccessful ones. It's clear we can achieve that if pt ≥ x and qt - pt ≥ y - x, since we can only increase both the number of successful and unsuccessful submissions.

Note that both inequalities have constant right hand side, and their left hand side doesn't decrease as t increases. Therefore, if the inequalities are satisfied for some t, they will definitely be satisfied for larger t as well.

It means we can apply binary search to find the lowest value of t satisfying the inequality. Then, the answer to the problem is qt - y. If even for very large t the inequalities are not satisfied, the answer is -1.

It can be proved that one "very large" value of t is t = y — that is, if the inequalities are not satisfied for t = y, then they cannot be satisfied for any value of t. Alternatively, picking t = 10⁹ works too, since y ≤ 10⁹.

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

bool check(ll x, ll y, ll p, ll q, ll t) {
  return p * t >= x && q * t - p * t >= y - x;
}

void solve() {
  ll x, y, p, q;
  scanf("%lld%lld%lld%lld", &x, &y, &p, &q);

  ll l = -1;
  ll r = (ll) 1e9;

  if (!check(x, y, p, q, r)) {
    printf("-1\n");
    return;
  }

  while (r - l > 1) {
    ll m = (l + r) / 2;
    if (check(x, y, p, q, m)) {
      r = m;
    } else {
      l = m;
    }
  }

  printf("%lld\n", r * q - y);
}

int main() {
  int t;
  scanf("%d", &t);

  while (t--) {
    solve();
  }

  return 0;
}

Read the binary search solution first.

Actually, inequalities pt ≥ x and qt - pt ≥ y - x are easy to solve by hand. From pt ≥ x it follows that 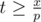. From qt - pt ≥ y - x it follows that 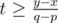. In order to satisfy both inequalities, t has to satisfy .

Don't forget that t has to be integer, so the division results have to be rounded up to the nearest integer. In general, if we want to find rounded up where both a and b are positive integers, the usual way to do that is to calculate (a + b - 1) / b, where " / " is the standard integer division (rounded down).

In this solution, cases when p / q = 0 / 1 or p / q = 1 / 1 have to be handled separately.

#include <bits/stdc++.h>

using namespace std;

int main() {
  int tt;
  cin >> tt;
  while (tt--) {
    int x, y, p, q;
    cin >> x >> y >> p >> q;
    if (p == 0) {
      cout << (x == 0 ? 0 : -1) << endl;
      continue;
    }
    if (p == q) {
      cout << (x == y ? 0 : -1) << endl;
      continue;
    }
    int t1 = (x + p - 1) / p;
    int t2 = ((y - x) + (q - p) - 1) / (q - p);
    cout << (q * 1LL * max(t1, t2) - y) << endl;
  }
  return 0;
}