[problem:A]

If the strings are the same, Any subsequence of a is indeed a subsequence of b so the answer is "-1", Otherwise the longer string can't be a subsequence of the other (If they are equal in length and aren't the same, No one can be a subsequence of the other) so the answer is maximum of their lengths.

Code :

Time complexity : O(|a| + |b|).

Problem author : me.

Solution author : me.

Testers : me and mahmoudbadawy.

[problem:B]

First solution :-

Let x, y and z be the lengths of 3 line segments such that x ≤ y ≤ z, If they can't form a non-degenerate triangle, Line segments of lengths x - 1, y and z or x, y and z + 1 can't form a non-degenerate triangle, So we don't need to try all the combinations, If we try y as the middle one, We need to try the maximum x that is less than or equal to y and the minimum z that is greater than or equal to y, The easiest way to do so is to sort the line segments and try every consecutive 3.

Code :

Time complexity : O(nlog(n)).

Second solution :-

Depending on the note from the first solution, If we try to generate a sequence such that after sorting, Every consecutive 3 line segments will form a degenerate triangle, It will be 1 1 2 3 5 8 13 ... which is Fibonacci sequence, Fibonacci is a fast growing sequence, fib(45) = 1134903170, Notice that Fibonacci makes maximum n with "NO" as the answer, That means the answer is indeed "YES" for n ≥ 45, For n < 45, You can do the naive O(n³) solution or the first solution.

Code :

Let x be the number that satisfies these inequalities:-

fib(x) ≤ maxAi.

fib(x + 1) > maxAi.

Time complexity : O(x³) or O(xlog(x)).

Problem author : me.

Solutions author : me.

Testers : me and mahmoudbadawy.

[problem:C]

Let dp[i] be the number of ways to split the prefix of s ending at index i into substrings that fulfills the conditions. Let it be 1-indexed. Our base case is dp[0] = 1. Our answer is dp[n]. Now let's calculate it for every i. Let l be the minimum possible index such that the substring from l to i satisfies the condition, Let x be a moving pointer, At the beginning x = i - 1 and it decreases, Every time we decrease x, We calculate the new value of l depending on the current character like that, l = max(l, i - a_s[x]). While x is greater than or equal to l we add dp[x] to dp[i], To find the longest substring, Find maximum i - x, To find the minimum number of substrings, there is an easy greedy solution, Find the longest valid prefix and delete it and do the same again until the string is empty, The number of times this operation is repeated is our answer, Or see the dynamic programming solution in the code.

Code :

Time complexity : O(n²).

Try to find an O(n) solution(I'll post a hard version of some problems on this blog soon).

Problem authors : me and mahmoudbadawy.

Solution authors : me and mahmoudbadawy.

Testers : me and mahmoudbadawy.

[problem:D]

Let's build a graph containing words, For every relation in the input add a new edge with the weight of 0 if they are equal and 1 if they are opposites, If adding the edge doesn't make the graph cyclic, Our relation is valid, Otherwise it may be valid or invalid. Check if adding that edge will make the graph cyclic or not using union-find like Kruskal's algorithm. Suspend answering relations that will make the graph cyclic, Now we have a forest of trees, Let cum[i] be the xor of the weights on the edges in the path from the root of the component of node i to node i. To find the relation between 2 words u and v, Check if they are in the same component using union-find, If they aren't the answer is 3 otherwise the answer is 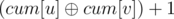, Now to answer suspended relations, Find the relation between the 2 words and check if it's the same as the input relation, Then answer the queries.

Time complexity for both solutions : O((n + m + q)log(n) * maxL) where maxL is the length of the longest string considering that union-find works in constant time.

Problem author : mahmoudbadawy.

Solution author : me.

[problem:E]

If we have an array ans[i] which represents the number of paths that makes the i^th bit sit to 1, Our answer is the sum of ans[i] * 2ⁱ for all i less than or equal to log(n). Now let's calculate this array.

Let arr[i][x] be the binary value of the x^th bit of the number attached to node i(just to make work easier). Let dp[i][x][j] be the number of paths starting from node i and ends at some node of the subtree of node i that makes the x^th bit of the xor sit to j. Our base case is the paths starting from the node and ending at the same node so for any i and x, dp[i][x][arr[i][x]] = 1. The path starting from node a to node b such that a ≠ b is the path starting from the child of a that is an ancestor of b with node a added to it so we can calculate our dp like that:-

Root the tree at node 1 and dfs, Let the current node be i, dp[i][x][j] +  = dp[k][x][j^arr[i][x]] where k loops on the children of i. Add dp[i][x][1] to ans[x]. Now that we have our dp, The naive way to complete the solution is to try every path with node i as the lca with this dp by looping over every 2 different children of node i but with some math you can realize that:-

Let s[i][x][j] be the sum of dp[k][x][j] where k loops over the children of node i.