Aim — To multiply 2 n-degree polynomials in 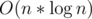 instead of the trivial O(n2)
instead of the trivial O(n2)
I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm. Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand for others struggling with fft.
Let’s get started - 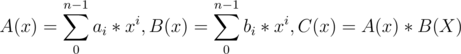 Here A(x) and B(x)are polynomials of degree n-1. Now we want to retrieve C(x) in O(n*logn)
Here A(x) and B(x)are polynomials of degree n-1. Now we want to retrieve C(x) in O(n*logn)
So our methodology would be this Convert A(x) and B(x) from coefficient form to point value form. (FFT) Now do theO(n) convulsion in point value form to obtain C(x) in point value form, ie. basically C(x) = A(x) * B(x) in point value form. Now convert C(x) from point value from to coefficient form (Inverse FFT).
Now, what is point value form ?






