586A - Alena's Schedule

The problem is prepared by adedalic.

В этой задаче сначала нужно было выкинуть все нули на префиксе и суффиксе строки, после чего ответ был равен количеству единиц плюс количество нулей с двух сторон от которых стоят единицы. Асимптотическая сложность решения: O(n).

586B - Laurenty and Shop

The problem is prepared by Oleg_Smirnov.

Назовем путь i-м (0 ≤ i ≤ n - 1), если мы, выходя из дома, сначала i раз идем налево, потом переходим проспект и снова n - 1 - i раз идем налево. Введем обозначение d_i — время, которое нам придется ждать на светофорах на i-м пути. Если рассмотреть путь из магазина домой с конца, то получится пути из дома в магазиг, поэтому искомый путь есть два разных пути из дома в магазин. Значит ответом на задачу является сумма наименьшего и второго по величине значения d_i. Значение d_i легко пересчитывается из значения d_i - 1, таким образом все d_i можно посчитать за один проход.

Асимптотическая сложность решения: O(n).

585A - Gennady the Dentist

The problem is prepared by Neon.

Заведем очередь в которой, будут находится дети. На каждой итерации решения пройдем по всем детям, если есть ребенок с отрицательной решимостью удалим его из очереди, а из решимостей детей с большими номерами вычтем d_i. Если все дети в очереди имеют решимость не меньше нуля, возьмем первого ребенка из очереди, а от решимостей остальных вычтем арифметическую прогрессию, как это описывается в условии.

Асимптотическая сложность решения: O(n²).

585B - Phillip and Trains

The problem is prepared by IlyaLos.

В задаче требовалось просто промоделировать игру. Это можно сделать с помощью обхода в глубину, ширину или динамического программирования. Состоянием является пара чисел x, y — позиция Филиппа в туннеле, а значением 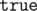или 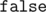в зависимости от того, можем ли мы попасть из стартовой позиции в x, y. Положения поездов в каждый момент времени определяются однозначно.

Асимптотическая сложность решения: O(n).

585C - Alice, Bob, Oranges and Apples

The problem is prepared by Edvard.

Поймем для начала, что означает процесс описанный в условии. Если нарисовать дерево переходов по буквам 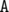и , то получится дерево Штерна-Броко. Пусть апельсины это значения знаменателя дроби, а яблоки — числителя. На каждом шагу у нас есть две дроби (изначально 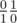) и мы заменяем либо первую дробь на их медианту, либо вторую. Таким образом, первая дробь есть первый предок влево от медианты, а вторая — первый предок вправо. Таким образом, искомый процесс это просто процесс поиска дроби в дереве Штерна-Броко, который завершается тем, что текущая медианта совпадает с дробью, которую мы ищем (момент окончания игры, описанный в условии). Значит, числа x, y заданные в условии это просто дробь, которую мы ищем. Отсюда следует, что ответа не существует, если x не взаимнопросто с y (поскольку таким дробей нет в дереве Штерна-Броко). Пусть теперь мы хотим найти дробь в дереве. Понятно, что если x > y, то мы сначала перейдем в правую ветку. Более того мы можем считать, что теперь ищем дробь 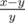и никуда не спускались. Если же x < y, то нам нужно спуситься в левую ветку и можно считать, что мы ищем дробь 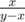и пока никуда не спускались. Эти рассуждения легко формализовать, чтобы получить строгое доказательство. Таким образом, решение задачи сводится к выполнению алгоритма Евклида для пары чисел x, y. Как известно время работы алгоритма Евклида O(logn) (дольше всего алгоритм Евклида работает на двух последовательных числах Фибоначчи), значит длина ответа тоже растет как логарифм.

Асимптотическая сложность решения: O(logn).

585D - Lizard Era: Beginning

The problem is prepared by danilka.pro.

Для решения этой задачи воспользуемся приемом 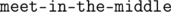. А именно переберем для первых 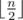(первая половина) заданий с какими спутницами главный герой будет путешествовать. Пусть при этом симпатия первой спутницы оказалась равна a, второй — b, а третьей c. Пусть существует способ выбрать спутниц для последующих 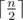(вторая половина) заданий так и пусть симпатии при этом будут равны a', b', c'. Тогда, чтобы по всем заданиям суммы симпатий были одинаковы необходимо и достаточно, чтобы a - b = b' - a и b - c = c' - b'. Теперь для решения задачи достаточно перебрать первую половину и сохранить в некоторой структуре данных тройки чисел a - b, b - c, a (третье число нужно для максимизации ответа в случае равенства). Далее нужно перебрать вторую половину и найти в структуре данных значения b' - a', c' - b', m, где m — максимальное третье значение которое есть в структуре данных. В качестве структуры данных можно использовать map < pair < int, int > , int >  в языке C++, первые два числа это значение a - b, b - c, а третье — максимальное a соответствующее первым двум. Также можно все тройки сложить в один большой массив, отсортировать его и бинарным поиском находить необходимые значения.

Асимптотическая сложность решения: 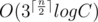, где logC — константа, появляющаяся вместе со структурой данных.

585E - Present for Vitalik the Philatelist

The problem is prepared by gridnevvvit.

Let's calculate the number of subsets with gcd equal to 1 — value A. Let's do that using principle of inclusions-exclusions: firstly we say that all subsets is good. The total number of subsets is equal to 2ⁿ. Now let's subtract subsets with gcd divisible by 2. The number of that subsets is equal to 2^cnt₂ - 1 (cnt_i is the number of numbers that is divisable by

Unable to parse markup [type=CF_TEX]

. Subsets with gcd divisible by 4 we already counted with number two. Next we should subtract 2^cnt₃ - 1. Now we should notice that subsets with gcd divisible by 6 we already processed twice: firstly with number 2, then with — 3, so let's add the number of these subsets 2^cnt₆ - 1. If we continue this process we will get, that for all numbers d we should add the value μ(d)(2^cnt_d - 1), where μ(d) is equals to 0, if d is divisible by square of some prime, 1, if the number of primes in factorization of d is even and  - 1 in other case. So the numbers that is divisible by square of some prime we can ignore, because they have coefficient 0. To calculate values cnt_i we should factorize all numbers and iterate over 2^k divisors with value μ(d) ≠ 0. Now it's easy to see, that the number of subsets with gcd greater than 1 equals to B = 2ⁿ - A. To solve the problem let's fix the stamp that Vitaliy will buy a_i. Let's recalculate the number B for array a without element a_i. To do that we should only subtract those terms that was affected by number a_i. We can do that in 2^k, where k is the number of primes in factorization of the number a_i. It's easy to see that only the subsets with gcd greater than 1, but not divisible by any divisor of a_i, should we counted in answer. To calculate number of those subsets let's again use the principle of inclusions-exclusions. For every divisor d of a_i let's subtract the value 2^cnt_d - 1 from B. So now we get B_i — the number of subsets with gcd greater than 1, but coprime with a_i. The answer to problem is the sum over all B_i. The maximum number of primes in factorization of number not greater than 10⁷ is equal to 8. We can factorize all numbers from 1 to n in linear time by algorithm for finding the smallest divisors for all intergers from 1 to n, or by sieve of Eratosthenes in O(nloglogn) time.

Complexity: O(C + n2^K), where 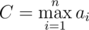, K — is the largest number of primes in factorization of a_i.

585F - Digits of Number Pi

The problem is prepared by Edvard.

Consider all substrings of string s with length 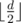. Let's add them all to trie data structure, calculate failure links and build automata by digits. We can do that in linear time using Aho-Korasik algorithm. Now to solve the problem we should calculate dp z_{i, v, b1, b2, b}. State of dp is described by five numbers: i — number of digits, that we already put to our number, v — in which vertex of trie we are, b₁ — equals to one if the prefix that we built is equals to prefix of x, b₂ — equals to one if the prefix that we built is equals to prefix of y, b — equals to one if we already have some substring with length 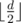on the prexif that we built. The value of dp is the number of ways to built prefix with the given set of properties. To update dp we should iterate over the digit that we want to add to prefix, check that we still is in segment [x, y], go from vertex v to the next vertex in automata. So the answer is sum by all v, b₁, b₂ z_{b, v, v1, v2, 1}.

Complexity: O(nd²).