Задачу подготовил adedalic.
В этой задаче сначала нужно было выкинуть все нули на префиксе и суффиксе строки, после чего ответ был равен количеству единиц плюс количество нулей с двух сторон от которых стоят единицы. Асимптотическая сложность решения: O(n).
Задачу подготовил Oleg_Smirnov.
Назовем путь i-м (0 ≤ i ≤ n - 1), если мы, выходя из дома, сначала i раз идем налево, потом переходим проспект и снова n - 1 - i раз идем налево. Введем обозначение di — время, которое нам придется ждать на светофорах на i-м пути. Если рассмотреть путь из магазина домой с конца, то получится пути из дома в магазиг, поэтому искомый путь есть два разных пути из дома в магазин. Значит ответом на задачу является сумма наименьшего и второго по величине значения di. Значение di легко пересчитывается из значения di - 1, таким образом все di можно посчитать за один проход.
Асимптотическая сложность решения: O(n).
Задачу подготовил Neon.
Заведем очередь в которой, будут находится дети. На каждой итерации решения пройдем по всем детям, если есть ребенок с отрицательной решимостью удалим его из очереди, а из решимостей детей с большими номерами вычтем di. Если все дети в очереди имеют решимость не меньше нуля, возьмем первого ребенка из очереди, а от решимостей остальных вычтем арифметическую прогрессию, как это описывается в условии.
Асимптотическая сложность решения: O(n2).
Задачу подготовил IlyaLos.
В задаче требовалось просто промоделировать игру. Это можно сделать с помощью обхода в глубину, ширину или динамического программирования. Состоянием является пара чисел x, y — позиция Филиппа в туннеле, а значением \texttt{true} или \texttt{false} в зависимости от того, можем ли мы попасть из стартовой позиции в x, y. Положения поездов в каждый момент времени определяются однозначно.
Асимптотическая сложность решения: O(n).
585C - Alice, Bob, Oranges and Apples
Задачу подготовил Edvard.
Поймем для начала, что означает процесс описанный в условии. Если нарисовать дерево переходов по буквам \texttt{A} и \texttt{B}, то получится дерево Штерна-Броко (https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%80%D0%B5%D0%B2%D0%BE_%D0%A8%D1%82%D0%B5%D1%80%D0%BD%D0%B0_%E2%80%94_%D0%91%D1%80%D0%BE%D0%BA%D0%BE). Пусть апельсины это значения знаменателя дроби, а яблоки — числителя. На каждом шагу у нас есть две дроби (изначально 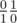 ) и мы заменяем либо первую дробь на их медианту, либо вторую. Таким образом, первая дробь есть первый предок влево от медианты, а вторая — первый предок вправо. Таким образом, искомый процесс это просто процесс поиска дроби в дереве Штерна-Броко, который завершается тем, что текущая медианта совпадает с дробью, которую мы ищем (момент окончания игры, описанный в условии). Значит, числа x, y заданные в условии это просто дробь, которую мы ищем. Отсюда следует, что ответа не существует, если x не взаимнопросто с y (поскольку таким дробей нет в дереве Штерна-Броко). Пусть теперь мы хотим найти дробь в дереве. Понятно, что если x > y, то мы сначала перейдем в правую ветку. Более того мы можем считать, что теперь ищем дробь
) и мы заменяем либо первую дробь на их медианту, либо вторую. Таким образом, первая дробь есть первый предок влево от медианты, а вторая — первый предок вправо. Таким образом, искомый процесс это просто процесс поиска дроби в дереве Штерна-Броко, который завершается тем, что текущая медианта совпадает с дробью, которую мы ищем (момент окончания игры, описанный в условии). Значит, числа x, y заданные в условии это просто дробь, которую мы ищем. Отсюда следует, что ответа не существует, если x не взаимнопросто с y (поскольку таким дробей нет в дереве Штерна-Броко). Пусть теперь мы хотим найти дробь в дереве. Понятно, что если x > y, то мы сначала перейдем в правую ветку. Более того мы можем считать, что теперь ищем дробь 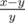 и никуда не спускались. Если же x < y, то нам нужно спуситься в левую ветку и можно считать, что мы ищем дробь
и никуда не спускались. Если же x < y, то нам нужно спуситься в левую ветку и можно считать, что мы ищем дробь 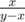 и пока никуда не спускались. Эти рассуждения легко формализовать, чтобы получить строгое доказательство. Таким образом, решение задачи сводится к выполнению алгоритма Евклида для пары чисел x, y. Как известно время работы алгоритма Евклида O(logn) (дольше всего алгоритм Евклида работает на двух последовательных числах Фибоначчи), значит длина ответа тоже растет как логарифм.
и пока никуда не спускались. Эти рассуждения легко формализовать, чтобы получить строгое доказательство. Таким образом, решение задачи сводится к выполнению алгоритма Евклида для пары чисел x, y. Как известно время работы алгоритма Евклида O(logn) (дольше всего алгоритм Евклида работает на двух последовательных числах Фибоначчи), значит длина ответа тоже растет как логарифм.
Асимптотическая сложность решения: O(logn).
Задачу подготовил danilka.pro.
Для решения этой задачи воспользуемся приемом \texttt{meet-in-the-middle}. А именно переберем для первых 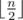 (первая половина) заданий с какими спутницами главный герой будет путешествовать. Пусть при этом симпатия первой спутницы оказалась равна a, второй — b, а третьей c. Пусть существует способ выбрать спутниц для последующих
(первая половина) заданий с какими спутницами главный герой будет путешествовать. Пусть при этом симпатия первой спутницы оказалась равна a, второй — b, а третьей c. Пусть существует способ выбрать спутниц для последующих 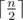 (вторая половина) заданий так и пусть симпатии при этом будут равны a', b', c'. Тогда, чтобы по всем заданиям суммы симпатий были одинаковы необходимо и достаточно, чтобы a - b = b' - a и b - c = c' - b'. Теперь для решения задачи достаточно перебрать первую половину и сохранить в некоторой структуре данных тройки чисел a - b, b - c, a (третье число нужно для максимизации ответа в случае равенства). Далее нужно перебрать вторую половину и найти в структуре данных значения b' - a', c' - b', m, где m — максимальное третье значение которое есть в структуре данных. В качестве структуры данных можно использовать map < pair < int, int > , int > в языке C++, первые два числа это значение a - b, b - c, а третье — максимальное a соответствующее первым двум. Также можно все тройки сложить в один большой массив, отсортировать его и бинарным поиском находить необходимые значения.
(вторая половина) заданий так и пусть симпатии при этом будут равны a', b', c'. Тогда, чтобы по всем заданиям суммы симпатий были одинаковы необходимо и достаточно, чтобы a - b = b' - a и b - c = c' - b'. Теперь для решения задачи достаточно перебрать первую половину и сохранить в некоторой структуре данных тройки чисел a - b, b - c, a (третье число нужно для максимизации ответа в случае равенства). Далее нужно перебрать вторую половину и найти в структуре данных значения b' - a', c' - b', m, где m — максимальное третье значение которое есть в структуре данных. В качестве структуры данных можно использовать map < pair < int, int > , int > в языке C++, первые два числа это значение a - b, b - c, а третье — максимальное a соответствующее первым двум. Также можно все тройки сложить в один большой массив, отсортировать его и бинарным поиском находить необходимые значения.
Асимптотическая сложность решения:  , где logC — константа, появляющаяся вместе со структурой данных.
, где logC — константа, появляющаяся вместе со структурой данных.
585E - Present for Vitalik the Philatelist
Задачу подготовил gridnevvvit.
Пусть мы хотим посчитать количество подмножеств с НОД равным 1 — число A. Посчитаем это количество с помощью формулы включений-исключений: сначала скажем, что все подмножества нам подходят. Таких подмножеств 2n. Теперь вычтем подмножества с НОД кратным 2. Количество таких множеств 2cnt2 - 1, где cnti — количество чисел, делящихся на i. Далее вычитаем 2cnt3 - 1. Подмножества с НОД кратным 4 мы учли вместе с двойкой. Далее вычитаем 2cnt5 - 1. Теперь заметим, что подмножества с НОД кратным 6 мы вычли уже дважды: сначала с двойкой, затем с тройкой, поэтому давайте прибавим количество таких подмножеств 2cnt6 - 1. Продолжая этот процесс получаем, что для числа d, к ответу нужно прибавить величину μ(d)(2cntd - 1), где μ(d) равно 0, если d делится на полный квадрат, 1, если количество простых в факторизации d четно и - 1 в противном случае. Значит числа, делящиеся на полный квадрат мы можем не суммировать, поскольку они входят с коэффициентом 0. Для подсчета значений cnti достаточно факторизовать все числа и для каждого за 2k перебрать делитель, со значением μ(d) ≠ 0. Теперь легко понять, что количество подмножеств с НОД большим 1 равно B = 2n - A. Теперь для решения задачи давайте переберем марку, которую купит Виталик ai. Пересчитаем число B так, как если бы числа ai не было в множестве. Для этого нужно просто вычесть те слагаемые на которые повлияло число ai. Это можно сделать за 2k, где k — количество простых в факторизации числа ai (снова нужно перебрать делители ai со значением μ(d) ≠ 0). Теперь поймем какие подмножества дадут НОД равный 1 вместе с выбранной маркой. Понятно это те подмножества НОД которых больше 1, но при этом не делится ни на один делитель ai. Для этого снова воспользуемся формулой включений-исключений. Для каждого делителя d числа ai вычтем из B значение 2cntd - 1. Таким образом, мы получим количество способов Bi выбрать подмножество c НОД большим 1, но при это взаимнопростым с ai. Ответом на задачу является сумма всех di. Наибольшее количество простых в факторизации числа не превосходящего 107 равно 8. Факторизацию чисел можно выполнить с помощью линейного алгоритма поиска минимального делителя чисел от 1 до n, либо с помощью решета Эратосфена за время O(nloglogn).
Асимптотическая сложность решения: O(C + n2K), где 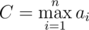 , а K — наибольшее количество простых в факторизации чисел ai.
, а K — наибольшее количество простых в факторизации чисел ai.
Задачу подготовил Edvard.
Расмотрим все подстроки строки s длины 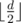 . Сложим все эти строки в бор, посчитаем суффиксные ссылки и построим автомат по цифрам. Это можно сделать за линейное время с помощью алгоритма Ахо-Корасик. Теперь для решения задачи посчитаем динамику zivb1b2b в котором состояние описывается пятеркой чисел: i — количество цифр которые мы уже поставили в искомом числе, которое встречается \texttt{наполовину}, v — в какой вершине бора мы находимся, b1 — равен ли префикс числа, которое мы набираем префиксу числа x, b2 — равен ли префикс числа, которое мы набираем префиксу числа y, b — находится ли некоторая подстрока длина
. Сложим все эти строки в бор, посчитаем суффиксные ссылки и построим автомат по цифрам. Это можно сделать за линейное время с помощью алгоритма Ахо-Корасик. Теперь для решения задачи посчитаем динамику zivb1b2b в котором состояние описывается пятеркой чисел: i — количество цифр которые мы уже поставили в искомом числе, которое встречается \texttt{наполовину}, v — в какой вершине бора мы находимся, b1 — равен ли префикс числа, которое мы набираем префиксу числа x, b2 — равен ли префикс числа, которое мы набираем префиксу числа y, b — находится ли некоторая подстрока длина 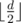 на уже набранном префиксе в боре (значения b1, b2, b — равны либо 0, либо 1). Значением динамики является количество способов набрать префикс с заданным набором свойств. Для того, чтобы сделать переход нужно перебрать цифру, проверить что мы не вышли за границы отрезка [x, y], перейти от вершины v к следующей вершине по автомату и заданной цифре. Ответом является сумма по всем v, b1, b2 zbvv1v21.
на уже набранном префиксе в боре (значения b1, b2, b — равны либо 0, либо 1). Значением динамики является количество способов набрать префикс с заданным набором свойств. Для того, чтобы сделать переход нужно перебрать цифру, проверить что мы не вышли за границы отрезка [x, y], перейти от вершины v к следующей вершине по автомату и заданной цифре. Ответом является сумма по всем v, b1, b2 zbvv1v21.
Асимптотическая сложность решения: O(nd2).







