Submission I would like to explain the logic used to solve problem E (which I didn't manage to complete during the contest and submitted shortly after).
For this, it will be useful to know what Catalan numbers are, as well as how to derive their formula. You can read about Catalan numbers in detail, for example, on wiki: тык, Catalan numbers can be defined in different ways, but we will define the number $$$C_n$$$ as the number of balanced bracket sequences of length $$$2n.$$$ We are interested in the following relatively well-known and elegant method to find this number.
Let’s consider a coordinate grid where we need to walk from $$$(0,0)$$$ to $$$(n,n)$$$. We can only move to the right or up. A step to the right corresponds to an opening bracket, and a step up — to a closing one. Thus, there is a one-to-one correspondence between a valid bracket sequence of length $$$2n$$$ and a path from $$$(0,0)$$$ to $$$(n,n)$$$ that does not cross the diagonal $$$y=x$$$; since a point above this diagonal would mean that in the current prefix, there are more closing brackets than opening ones. How can we find the number of such paths?
The total number of paths is $$$\binom{2n}{n}.$$$ From this number, we subtract the number of invalid paths. Invalid paths are those that cross $$$y=x$$$, or, equivalently, have at least one common point with the line $$$y=x+1.$$$ Take the first (with the smallest $$$x$$$) common point $$$(a, a+1)$$$ and reflect the segment of the path from $$$(0,0)$$$ to $$$(a, a+1)$$$ across the line $$$y=x+1.$$$ We obtain a path from $$$(-1,1)$$$ to $$$(n,n)$$$. This is a one-to-one correspondence. Indeed, any path starting at $$$(0,0)$$$ that has common points with $$$y=x+1$$$ can be reflected up to the first such point. At the same time, any path from $$$(-1,1)$$$ to $$$(n,n)$$$ must have common points with с $$$y=x+1$$$, since the start and end points of the path are on opposite sides of the line, which means we can also reflect the segment of the path up to the first such point. The number of such invalid paths is $$$\binom{2n}{n+1}.$$$ (or, equivalently $$$\binom{2n}{n-1}.$$$) Therefore, the number of valid paths is $$$C_n = $$$\binom{2n}{n} — $$$\binom{2n}{n+1}.$$$ Это и есть число Каталана. Подробнее на картинке. 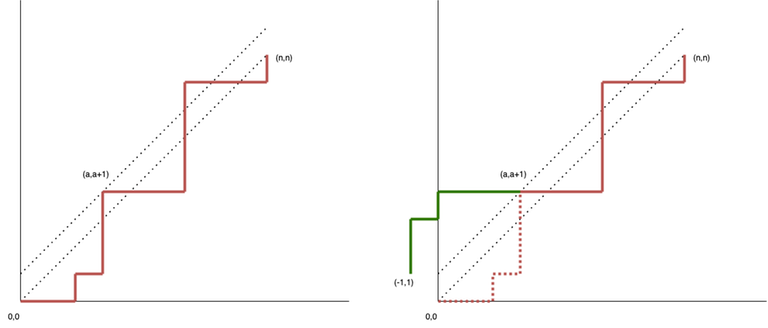
Если бы в задаче не было козырной масти, выигрышное распределение карт между игроками удовлетворяло бы условию что все карты одной масти распределены в порядке правильной скобочной последовательности, по $$$m/2$$$ карт у каждого игрока. Однако наличие козыря потребует от нас двух модификаций для формулу выше.
Во-первых, масть 1 по-прежнему должна удовлетворять условию префикса правильной скобочной последовательности, однако она не обязана быть оконченной. Любой путь из $$$(0,0)$$$ в $$$(a, m-a), a \ge m-a$$$, не пересекающий $$$y=x$$$ удовлетворяет условию. Количество таких путей $$$\binom{m}{a} - \binom{m}{a+1}$$$. Такое распределение мастей оставит нам $$$2a - m$$$ козырей, которые мы можем потратить на дальнейшие масти. Это будет базой нашего ДП. Пусть $$$dp_i[ta]$$$ — количество способов расположить выигрышным образным первые $$$i$$$ мастей, оставив в запасе $$$ta$$$ козырных карт. Тогда $$$dp_1[2a - m] = \binom{m}{a} - \binom{m}{a+1} \forall a \ge m/2.$$$
Во-вторых если мы тратим на масть $$$i \ne 1$$$ $$$k$$$ козырей (это число может быть только четным), это означает что игрок 1 выкладывает $$$(m - k)/2$$$ карт масти $$$i$$$ а игрок 2 — $$$(m+k)/2$$$ карт. При этом карты должны удовлетворять условию "не слишком неправильной" скобочной последовательности, а именно, на любом префиксе количество закрывающихся скобок не должно превышать количество открывающихся больше чем на $$$k.$$$
Соединив эти мысли, получаем что результат — количество путей из $$$(0,0)$$$ в $$$(\frac{m - k}{2}, \frac{m + k}{2})$$$, не пересекающих $$$y = x + k$$$. Плохие пути отражаются аналогичным образом, но относительно прямой $$$y = x + k + 1$$$, в пути стартующие в $$$( -(k+1), (k+1))$$$. Таким образом количество хороших путей $$$f(m,k) = \binom{m}{(m - k)/2} - \binom{m}{(m - k)/2 + k + 1}$$$. 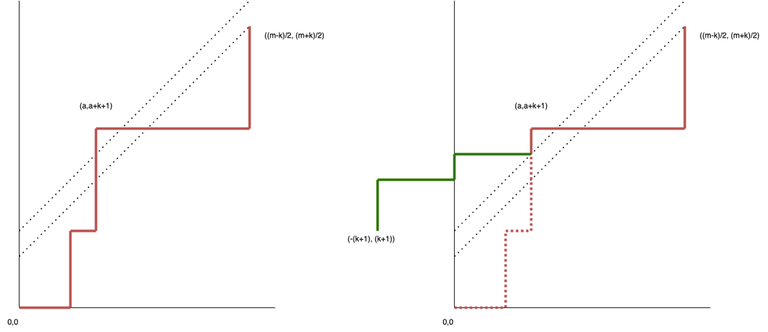
Сам переход ДП несложный: $$$\forall ta \le m, \forall k \le ta, dp_i[ta - k] += f(m,k)*dp_{i-1}[ta].$$$ Достаточно итерироваться только по четным $$$ta$$$ и $$$k$$$. Сложность $$$O(m^2n).$$$






