###Introduction↵
A classical problem reads:↵
↵
> Count the paths from $(0,0)$ to $(m,n)(n>m>0)$ that doesn't go through $y=x$ (the path can touch the line). One can only move up or right by $1$ in one move.↵
↵
The problem can also be described as:↵
↵
> Count binary strings that consist of $m$ zeros and $n$ ones $(n\ge m)$, such that in every prefix of the string, the number of zeros doesn't exceed the number of ones.↵
↵
Consider how to count paths from $(0,0)$ to $(m,n)$ without the intersection restriction. To get to $(m,n)$, we must move up $n$ times and move right $m$ times. In other words, we need to permute $n$ right and $m$ up, whose quantity is↵
↵
$$\displaystyle{\frac{(m+n)!}{m!n!}=\binom{m+n}{m}}$$↵
↵
Tocount the paths that doesn't intersectfind the answer, we can try to count the paths that go through $y=x$, and this is when the reflection principle is utilized. The principle says:↵
↵
> Given point $A,B$ at the same side of line $l$, the number of paths from $A$ to $B$ that intersect with $l$ is equal to that of paths from $A^\prime$ to $B$, where $A^\prime$ is the reflection point through $l$.↵
↵
To show why it is correct, we should first note that a path from $A^\prime$ to $B$ must intersect with $y=x$. Say at point $P$ the path first intersect with $y=x$, we can reflect the path from $A^\prime$ to $P$ through $l$ and get a path from $A$ to $B$, and vice versa. This indicates that the intersecting paths from $A$ to $B$ and the paths from $A^\prime$ and $B$ are one-to-one corresponded, and the quantity of the two are the same.↵
↵
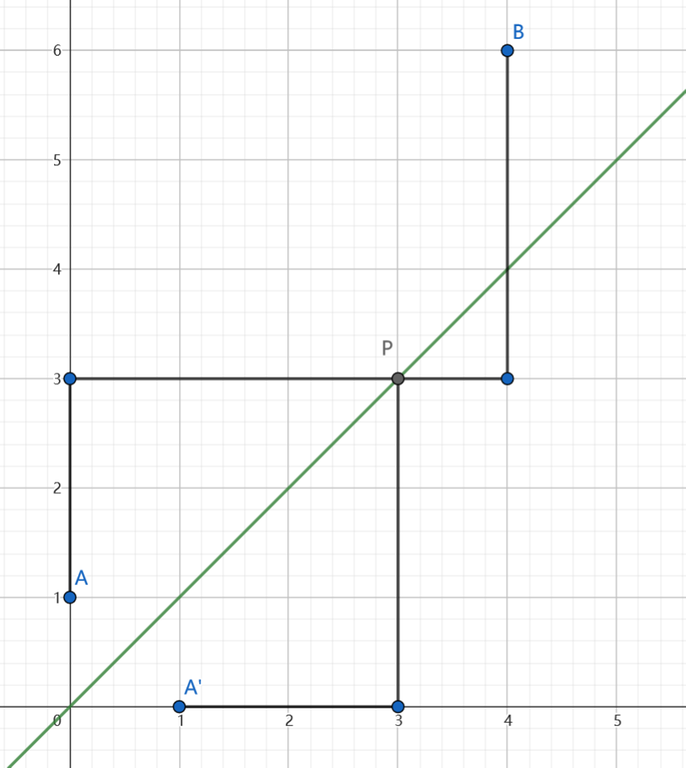↵
↵
Back to our problem. Going through $y=x$ is the same as intersecting with $y=x-1$ in this case, so $(0,0)$ can reflected to $(1,-1)$, and the number of intersecting path is $\binom{m+n}{m-1}$. Therefore, the answer to the problem is↵
↵
$$\boxed{\displaystyle{\binom{m+n}{m}-\binom{m+n}{m-1}=\frac{n-m+1}{n+1}\binom{m+n}{m}}}$$↵
↵
In particular, when $n=m$, the formula becomes↵
↵
$$\boxed{\displaystyle{\frac{1}{n+1}\binom{2n}{n}}}$$↵
↵
which is the **Catalan number**.↵
↵
<spoiler summary="Note">↵
Note that there are two ways to generate valid paths in the first description when $n=m$, one keeps $x\ge y$ and the other keeps $x\le y$, so the answer is $\frac{2}{n+1}\binom{2n}{n}$.↵
</spoiler>↵
↵
###Examples↵
[problem:26D]↵
↵
<spoiler summary="Tutorial">↵
If one buys a ticket with only a 20 euro banknote, Charlie should use a 10 euro banknote for change. Say Charlie has served $x$ customers with only 20 euro and $y$ with only 10 euro, the inequality $y\ge x-k$ must hold to keep the process run.↵
↵
Therefore, the not-intersected line in this question is $y=x-k-1$ and $(0,0)$ reflects to $(k+1,-k-1)$, which gives the number of good permutations as:↵
↵
$$\displaystyle{\binom{m+n}{m}-\binom{m+n}{m-k-1}}$$↵
↵
And the answer to this problem is:↵
↵
$$\boxed{\displaystyle{1-\frac{\binom{m+n}{m-k-1}}{\binom{m+n}{m}}}}$$↵
</spoiler>↵
↵
[problem:105390D]↵
↵
<spoiler summary="Tutorial">↵
Suppose the printer does the operation 2 for $i$ times and does the operation 1 for the other $m-i$ times. Since the string only has $n$ characters, we must use $m-i-n$ operation 2 to clear extra characters. And now we have $k=i-(m-i-n)$ extra operations 2 which must be used on empty string to waste them.↵
↵
Now we suppose the printer does $x$ operation 2 and $y$ operation 1 at some time, and we can find the same inequality $y\ge x-k$ also holds. In addition, the equality $y=x-k$ must hold at a certain time. In other words, the path mustintersect wittouch $y=x-k$ but cannot go through it.↵
↵
To find the answer, we first find the number of non-intersect paths, which is $\binom{n}{i}-\binom{n}{i-k-1}$, and then find the number of non-go-through paths, which is $\binom{n}{i}-\binom{n}{i-k}$. Note that our pathsare intersects but not goes through with the line, so the number of our paths is that of non-go-through ones minus non-intersect ones, or↵
↵
$$\boxed{\displaystyle{\binom{n}{i-k}-\binom{n}{i-k-1}}}$$↵
↵
The problem can be easily solved by enumerating $i$ and accumulating results.↵
</spoiler>↵
↵
[problem:2025E]↵
↵
<spoiler summary="Tutorial">↵
Note that player 1 must have no less suit 1 cards (or trumps) than player 2, and of each other suits, player 1 must have no more cards (or non-trumps) than player 2. Particularly, player 1 uses his small trumps to ruff extra non-trumps of player 2. ↵
↵
Say $m=2p$ and in a distribution, player 1 has $p-q_i$ cards of suit $i(i\neq1)$, so player 2 has $p+q_i$ cards. We can list $1$ or $2$ according to the cards' ranks of two players. For example, if player 1 obtains $\{3,6\}$ and player 2 obtains $\{1,2,4,5\}$, the list is $221221$. To ensure each of player 1's cards finds an opponent's distinct card whose rank is below it, the list must satisfy that in each prefix of our list, the number of $2$ must be no less than $1$.↵
↵
Therefore, we can just substitude $m=p-q_i$ and $n=p+q_i$ into the formula above and get the number of valid distributions of this suit:↵
↵
$$\boxed{\displaystyle{a[q_i]=\frac{2q_i+1}{p+q_i+1}\binom{2p}{p-q_i}}}$$↵
↵
For suit 1, the formula is the same, i. e., when player 1 has $p+q_1$ trump card and player 2 has $p-q_1$, there are also $a\[q_1\]$ valid distributions.↵
↵
Enumerate $q_1$. Since $\sum_{i=2}^n q_i=q_1$, the number of other suits' distribution is $a^{*(n-1)}\[q_1\]$, so the final answer is:↵
↵
$$\boxed{\displaystyle{\sum_{q=0}^pa[q]a^{*(n-1)}[q]}}$$↵
</spoiler>↵
↵
A classical problem reads:↵
↵
> Count the paths from $(0,0)$ to $(m,n)(n>m>0)$ that doesn't go through $y=x$ (the path can touch the line). One can only move up or right by $1$ in one move.↵
↵
The problem can also be described as:↵
↵
> Count binary strings that consist of $m$ zeros and $n$ ones $(n\ge m)$, such that in every prefix of the string, the number of zeros doesn't exceed the number of ones.↵
↵
Consider how to count paths from $(0,0)$ to $(m,n)$ without the intersection restriction. To get to $(m,n)$, we must move up $n$ times and move right $m$ times. In other words, we need to permute $n$ right and $m$ up, whose quantity is↵
↵
$$\displaystyle{\frac{(m+n)!}{m!n!}=\binom{m+n}{m}}$$↵
↵
To
↵
> Given point $A,B$ at the same side of line $l$, the number of paths from $A$ to $B$ that intersect with $l$ is equal to that of paths from $A^\prime$ to $B$, where $A^\prime$ is the reflection point through $l$.↵
↵
To show why it is correct, we should first note that a path from $A^\prime$ to $B$ must intersect with $y=x$. Say at point $P$ the path first intersect with $y=x$, we can reflect the path from $A^\prime$ to $P$ through $l$ and get a path from $A$ to $B$, and vice versa. This indicates that the intersecting paths from $A$ to $B$ and the paths from $A^\prime$ and $B$ are one-to-one corresponded, and the quantity of the two are the same.↵
↵
↵
↵
Back to our problem. Going through $y=x$ is the same as intersecting with $y=x-1$ in this case, so $(0,0)$ can reflected to $(1,-1)$, and the number of intersecting path is $\binom{m+n}{m-1}$. Therefore, the answer to the problem is↵
↵
$$\boxed{\displaystyle{\binom{m+n}{m}-\binom{m+n}{m-1}=\frac{n-m+1}{n+1}\binom{m+n}{m}}}$$↵
↵
In particular, when $n=m$, the formula becomes↵
↵
$$\boxed{\displaystyle{\frac{1}{n+1}\binom{2n}{n}}}$$↵
↵
which is the **Catalan number**.↵
↵
<spoiler summary="Note">↵
Note that there are two ways to generate valid paths in the first description when $n=m$, one keeps $x\ge y$ and the other keeps $x\le y$, so the answer is $\frac{2}{n+1}\binom{2n}{n}$.↵
</spoiler>↵
↵
###Examples↵
[problem:26D]↵
↵
<spoiler summary="Tutorial">↵
If one buys a ticket with only a 20 euro banknote, Charlie should use a 10 euro banknote for change. Say Charlie has served $x$ customers with only 20 euro and $y$ with only 10 euro, the inequality $y\ge x-k$ must hold to keep the process run.↵
↵
Therefore, the not-intersected line in this question is $y=x-k-1$ and $(0,0)$ reflects to $(k+1,-k-1)$, which gives the number of good permutations as:↵
↵
$$\displaystyle{\binom{m+n}{m}-\binom{m+n}{m-k-1}}$$↵
↵
And the answer to this problem is:↵
↵
$$\boxed{\displaystyle{1-\frac{\binom{m+n}{m-k-1}}{\binom{m+n}{m}}}}$$↵
</spoiler>↵
↵
[problem:105390D]↵
↵
<spoiler summary="Tutorial">↵
Suppose the printer does the operation 2 for $i$ times and does the operation 1 for the other $m-i$ times. Since the string only has $n$ characters, we must use $m-i-n$ operation 2 to clear extra characters. And now we have $k=i-(m-i-n)$ extra operations 2 which must be used on empty string to waste them.↵
↵
Now we suppose the printer does $x$ operation 2 and $y$ operation 1 at some time, and we can find the same inequality $y\ge x-k$ also holds. In addition, the equality $y=x-k$ must hold at a certain time. In other words, the path must
↵
To find the answer, we first find the number of non-intersect paths, which is $\binom{n}{i}-\binom{n}{i-k-1}$, and then find the number of non-go-through paths, which is $\binom{n}{i}-\binom{n}{i-k}$. Note that our paths
↵
$$\boxed{\displaystyle{\binom{n}{i-k}-\binom{n}{i-k-1}}}$$↵
↵
The problem can be easily solved by enumerating $i$ and accumulating results.↵
</spoiler>↵
↵
[problem:2025E]↵
↵
<spoiler summary="Tutorial">↵
Note that player 1 must have no less suit 1 cards (or trumps) than player 2, and of each other suits, player 1 must have no more cards (or non-trumps) than player 2. Particularly, player 1 uses his small trumps to ruff extra non-trumps of player 2. ↵
↵
Say $m=2p$ and in a distribution, player 1 has $p-q_i$ cards of suit $i(i\neq1)$, so player 2 has $p+q_i$ cards. We can list $1$ or $2$ according to the cards' ranks of two players. For example, if player 1 obtains $\{3,6\}$ and player 2 obtains $\{1,2,4,5\}$, the list is $221221$. To ensure each of player 1's cards finds an opponent's distinct card whose rank is below it, the list must satisfy that in each prefix of our list, the number of $2$ must be no less than $1$.↵
↵
Therefore, we can just substitude $m=p-q_i$ and $n=p+q_i$ into the formula above and get the number of valid distributions of this suit:↵
↵
$$\boxed{\displaystyle{a[q_i]=\frac{2q_i+1}{p+q_i+1}\binom{2p}{p-q_i}}}$$↵
↵
For suit 1, the formula is the same, i. e., when player 1 has $p+q_1$ trump card and player 2 has $p-q_1$, there are also $a\[q_1\]$ valid distributions.↵
↵
Enumerate $q_1$. Since $\sum_{i=2}^n q_i=q_1$, the number of other suits' distribution is $a^{*(n-1)}\[q_1\]$, so the final answer is:↵
↵
$$\
</spoiler>↵
↵





