Hola Codeforces community! Sorry for the delay, we were solving some details of our national contest. We hope you enjoyed and learned a lot from this contest, we made it with much love. Our team worked day and night these last days to make sure you had a valuable experience :)). If you have any doubts about the editorial, please let us know in the comments, we are happy to help you. The editorial was prepared by jampm and me. Btw, best meme of the round.
2022A - Автобус в Пенхамо
2022B - Продавец Карел
include <bits/stdc++.h>
using namespace std;
int main() { int t; cin>>t; while(t--) { long long n,x; cin>>n>>x; vectorarr(n); long long sum=0; long long maximo=0; for(int k=0;k<n;k++) { cin>>arr[k]; maximo=max(maximo,arr[k]); sum+=arr[k]; } long long sec=(sum+x-1)/(long long)x; cout<<max(maximo,sec)<<endl; } } ```
2022C - Джерримендеринг
An important observation is that if you use a horizontal piece in one row, you also have to use it in the other to avoid leaving holes.
- $$$j = 0$$$: All cells up to the $$$i$$$-th column are completely filled (including $$$i$$$-th).
- $$$j = 1$$$: All cells up to the i-th column are completely filled (including $$$i$$$-th), and there’s one extra cell filled in the first row of the next column. $$$j = 2$$$: The $$$i$$$-th column is filled, and there’s one extra cell filled in the second row of the next column.
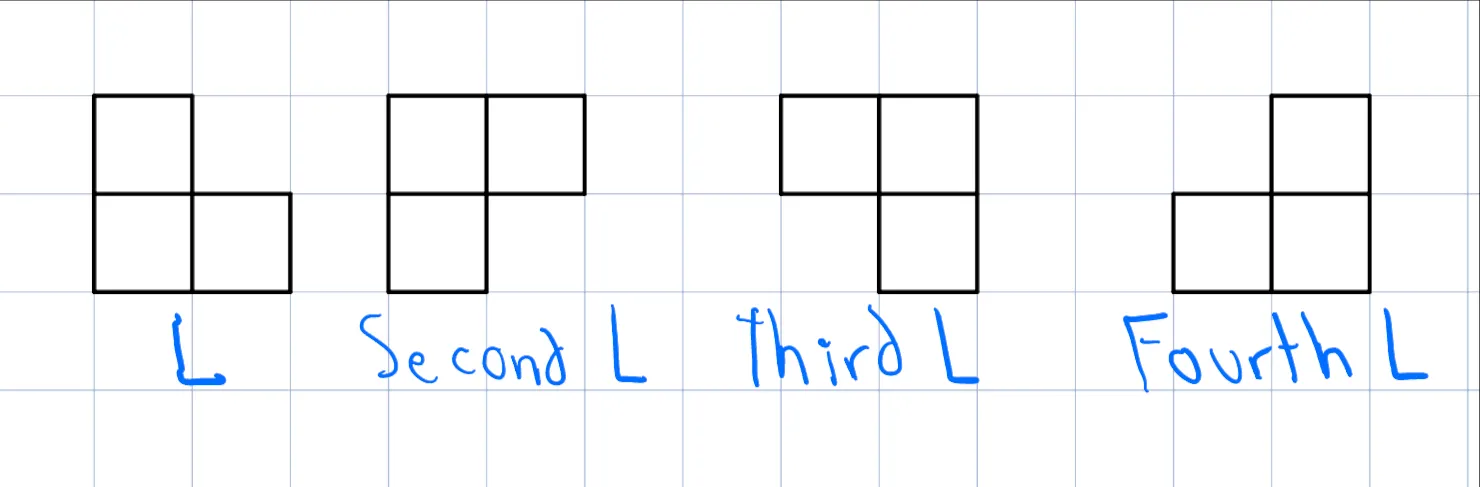
- From $$$dp[k][0]$$$ (Both rows filled at column $$$k$$$):
- You can place a horizontal piece in both rows, leading to $$$dp[k+3][0]$$$.
- You can place a first L piece, leading to $$$dp[k+1][1]$$$.
- You can place an L piece, leading to $$$dp[k+1][2]$$$.
- From $$$dp[k][1]$$$ (One extra cell in the first row of the next column):
- You can place a horizontal piece in the first row occupying from $$$k+2$$$ to $$$k+4$$$ and also a horizontal piece in the second row from $$$k+1$$$ to $$$k+3$$$, leading to $$$dp[k+3][1]$$$.
- You can place a fourth L, leading to $$$dp[k+2][0]$$$.
- From $$$dp[k][2]$$$ (One extra cell in the second row of the next column):
- You can place a horizontal piece in the first row occupying from $$$k+1$$$ to $$$k+3$$$ and also a horizontal piece in the second row from $$$k+2$$$ to $$$k+4$$$, leading to $$$dp[k+3][2]$$$.
- You can place a third L, leading to $$$dp[k+2][0]$$$.
From $$$dp[k][0]$$$:
From $$$dp[k][1]$$$:
From $$$dp[k][2]$$$:
To implement the DP solution, you only need to handle the transitions for states $$$dp[i][0]$$$ and $$$dp[i][1]$$$. For $$$dp[i][2]$$$, the transitions are the same as $$$dp[i][1]$$$, with the rows swapped.
```
2022D1 - Ассасин (простая версия)
Combining hint 2 with our solutions for $$$n = 3$$$ and $$$n = 4$$$, we can come up with the following algorithm:
While $$$n > 4$$$,
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- If their answers don't match, $$$n$$$ is the impostor.
- Otherwise, $$$n - 1$$$ is the impostor.
- If the answers match, do $$$n -= 2$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
If $$$n > 4$$$ doesn't hold and we haven't found the impostor, we either have the $$$n = 3$$$ case or the $$$n = 4$$$ case, and we can solve either of them in $$$4$$$ queries.
In the worst case, this algorithm uses $$$n + 1$$$ queries. I'm also aware of a solution with $$$n + 4$$$ queries, $$$n + 2$$$ queries, and one with $$$n + \lceil\log(n)\rceil$$$ queries. We only present this solution to shorten the length of the blog but feel free to ask about the others in the comments.
Code: 286031430
2022D2 - Ассасин (сложная версия)

If those two nodes are different, call $$$A$$$ the node with in-degree $$$0$$$ and $$$B$$$ the node with out-degree $$$0$$$. Let the grader always reply yes to your queries.
- $$$A$$$ can be the impostor and everyone else Knaves.
- $$$B$$$ can be the impostor and everyone else Knights.
If those two nodes are the same, then the graph looks like a collection of cycles and one isolated node. The grader will always reply yes except for the last query where it replies no. Let the last query be to player $$$A$$$ about player $$$B$$$. The two assignments of roles are:
- $$$A$$$ is the impostor and everyone else in the cycle is a Knight.
- $$$B$$$ is the impostor and everyone else in the cycle is a Knave.
Consider the natural directed graph representation, adding a directed edge with weight $$$0$$$ between node $$$i$$$ and $$$j$$$ if the answer to the query ''? i j'' was yes, and a $$$1$$$ otherwise. We will also denote this query by $$$i \mapsto j$$$.
We will use a lemma, that generalizes the idea for D1.
Lemma:
The sum of weights of a cycle is odd if and only if the impostor is among us (among the cycle, I mean).
The new graph is bipartite, and thus has an even number of edges. But all the edges in this new graph, are all the grey edges in the original graph, which implies what we want.
If the impostor is in the cycle, there are three ways of inserting it (assume the cycle has more than $$$2$$$ nodes that case is exactly what we proved in hint 2).
- We can insert the impostor into one of this ``segments'' of consecutive nodes with the same role. This would increase the number of grey edges by $$$1$$$, changing the parity,
- We can insert it between two segments.
- If we have Knight $$$\mapsto$$$ Impostor $$$\mapsto$$$ Knave, the number of grey edges decreases by $$$1$$$.
- If thee is Knave $$$\mapsto$$$ Impostor $$$\mapsto$$$ Knight, the number of grey edges increases by $$$1$$$.
Either way, we changed the parity of the cycle. $$$\blacksquare$$$
The algorithm that solves the problem is the following:
If $$$n = 3$$$,
query $$$1 \mapsto 2$$$ and $$$2 \mapsto 1$$$,
If queries match, $$$3$$$ is the impostor.
Else, query $$$1 \mapsto 3$$$ and $$$3 \mapsto 1$$$.
- If queries match, $$$2$$$ is the impostor.
- Else, $$$1$$$ is the impostor.
Else, $$$n > 3$$$. To solve $$$n > 3$$$ players with $$$n$$$ queries, do:
While $$$n > 5$$$,
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- If their answers don't match, $$$n$$$ is the impostor.
- Otherwise, $$$n - 1$$$ is the impostor.
- If the answers match, do $$$n -= 2$$$.
- If their answers don't match, one of them is the impostor. Query $$$n \mapsto n - 2$$$ and $$$n - 2 \mapsto n$$$.
- query $$$n \mapsto n - 1$$$ and $$$n - 1 \mapsto n$$$.
If $$$n > 5$$$ doesn't hold and we haven't found the impostor, we either have the $$$n = 4$$$ case or the $$$n = 5$$$ case, we solve them optimally in $$$4$$$ or $$$5$$$ queries each.
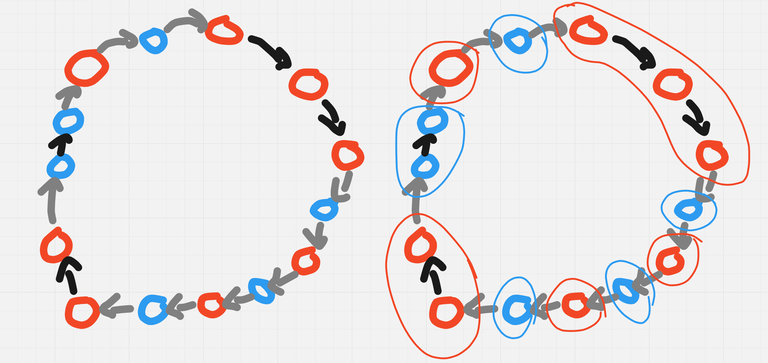
To solve $$$n = 5$$$ in $$$5$$$ queries,
We will form a cycle of size $$$3$$$, asking for $$$1 \mapsto 2$$$, $$$2 \mapsto 3$$$ and $$$3 \mapsto 2$$$ (blue edges in the image below).
- If the cycle has an even number of no's, we know the impostor is among $$$4$$$ or $$$5$$$. So we ask $$$3 \mapsto 4$$$ and $$$4 \mapsto 3$$$ (green edges).
- If both queries match, $$$5$$$ is the impostor.
- Else, $$$4$$$ is the impostor.
- Else, The impostor is among us (among the cycle, I mean). Ask $$$1 \mapsto 3$$$ and $$$2 \mapsto 1$$$ (purple edges).
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$1$$$ is the impostor.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, $$$2$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$3$$$ is the impostor.
- It is impossible for $$$1 \mapsto 2$$$ to match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ to match with $$$3 \mapsto 1$$$, because we know at least one of this cycles will contain the impostor.
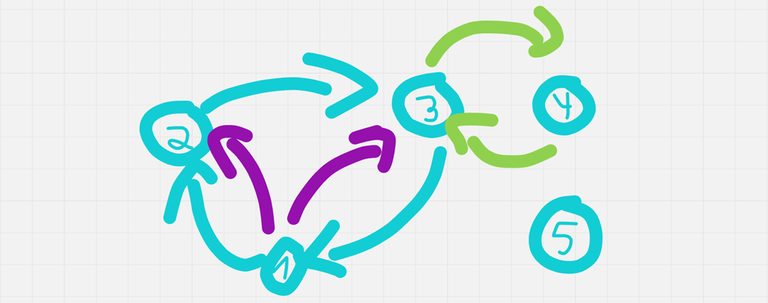
To solve $$$n = 4$$$ in $$$4$$$ queries,
We will query $$$1 \mapsto 2$$$, $$$2 \mapsto 1$$$, $$$1 \mapsto 3$$$ and $$$3 \mapsto 1$$$.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$1$$$ is the impostor.
- If $$$1 \mapsto 2$$$ doesn't match with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, $$$2$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ doesn't match with $$$3 \mapsto 1$$$, $$$3$$$ is the impostor.
- If $$$1 \mapsto 2$$$ matches with $$$2 \mapsto 1$$$ and $$$1 \mapsto 3$$$ matches with $$$3 \mapsto 1$$$, then $$$4$$$ is the impostor.
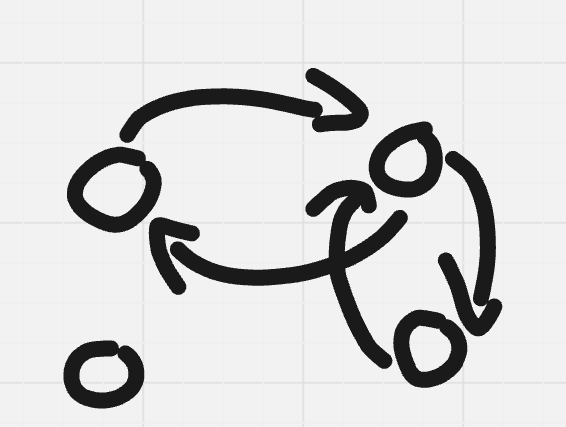
We have proven that that $$$f(n) \le \max(4, n)$$$. Now we will prove that $$$n \le f(n)$$$.
Consider the directed graph generated from the queries. By pigeonhole principle at least one node has in-degree $$$0$$$, and at least one node has out-degree $$$0$$$.
If those two nodes are different, call $$$A$$$ the node with in-degree $$$0$$$ and $$$B$$$ the node with out-degree $$$0$$$. Let the grader always reply yes to your queries.
- $$$A$$$ can be the impostor and everyone else Knaves.
- $$$B$$$ can be the impostor and everyone else Knights.
If those two nodes are the same, then the graph looks like a collection of cycles and one isolated node. The grader will always reply yes except for the last query where it replies no. Let the last query be to player $$$A$$$ about player $$$B$$$. The two assignments of roles are:
- $$$A$$$ is the impostor and everyone else in the cycle is a Knight.
- $$$B$$$ is the impostor and everyone else in the cycle is a Knave.
Thus, we have shown that regardless what the questions asked are, it is impossible to find the impostor among $$$n$$$ players, in $$$n - 1$$$ queries. $$$\blacksquare$$$
Now, we prove that $$$f(3) = 4$$$:

lol,
Actually, one of the testers coded the exhaustive checker. I will let them post their code if they want to.
Do small cases! Let the pencil (or the computer) do the work and use your brain to look out for patterns.
Try to find the most natural and simple way of modeling the problem.
Learn how to code a decision tree, or other models to exhaustively search for constructions, proof patterns, recursive complete search, etc. and build intuition on that to solve the more general cases of the problem.
2022E1 - Billetes MX (простая версия)
- That is, for each row, and each column, fix the first element, and change every value in that row or column by their xor with the first element.
We will be left with a grid whose first row and first column are all zeros.
But this grid also satisfies the condition! So it must hold that $$$a[i][j] \oplus a[i][0] \oplus a[0][j] \oplus a[0][0] = 0$$$, but 3 of this values are zero!
We can conclude that $$$a[i][j]$$$ must also be zero. This shows that there must exist two arrays $$$X$$$ and $$$Y$$$, such that $$$a[i][j] = X[i] \oplus Y[j]$$$, for any valid full grid.
This is just the solution. Please read the hints in order to understand why it works and how to derive it.
Precompute an array $$$c$$$, with $$$c[i] = 2^{30\cdot i} \pmod{10^9 + 7}$$$.
Let $$$a$$$ be the 2d array with known values of the grid. Consider the graph formed by adding an edge between node $$$i$$$ and node $$$j + n$$$ and weight $$$a[i][j]$$$ for every known tile $$$(i, j)$$$ in the grid. Iterate from $$$1$$$ to $$$n + m$$$ maintaining an array $$$p$$$ initialized in $$$-1$$$s. If the current proceed node hasn't been visited, we run a dfs through it. We will use array $$$p$$$ to maintain the running xor for each node during the dfs. If we ever encounter a back edge between nodes $$$u, v$$$ and weight $$$w$$$, we check if $$$p[u] \oplus p[v] = w$$$. If not, we the answer is zero. If this condition always holds, let $$$K$$$ be the number of times you had to run the dfs. $$$K$$$ is also the number of connected components in the graph. The answer is $$$c[K - 1]$$$.
Complexity: $$$\mathcal{O}(n + m + k)$$$.
Code: 285962028
2022E2 - Billetes MX (сложная версия)
Please read the solution to E1 beforehand, as well as all the hints.
The edges are never removed, so whenever an edge is added that creates a cycle with xor distinct to zero, this cycle will stay in the graph for all following updates. So we can binary search the first addition that creates a cycle with xor distinct to zero, using the same dfs we used in E1. After the first such edge, the answer will always be zero.
Now, for all the additions before that, we must determine how many connected components the graph has at each step. But this is easily solvable with Disjoint Set Union.
Complexity: $$$\mathcal{O}(\log(q)(n + m + k + q) + \alpha(n + m)(q + k))$$$.
Code: 285961673
We will answer the queries online. Remember that if the graph only contains cycles with xor $$$0$$$, the xor of a path between a pair of nodes is unique. We'll use this in our advantage. Let $$$W(u, v)$$$ be the unique value of the xor of a path between nodes $$$u$$$ and $$$v$$$.
Lets modify a dsu, drop the path compression, and define array $$$p$$$, that maintains the following invariant:
For every node $$$u$$$ in a component with root $$$r$$$, $$$W(u, r)$$$ equals the xor of $$$p[x]$$$ for all ancestors $$$x$$$ of $$$u$$$ in our dsu (we also consider $$$u$$$ an ancestor of itself).
Whenever we add an edge between two nodes $$$u$$$ and $$$v$$$ in two different components with weight $$$w$$$, we consider consider the roots $$$U$$$ and $$$V$$$ of their respective components. Without loss of generality, assume $$$U$$$'s component has more elements than $$$V$$$'s. We will add an edge with weight $$$W(u, U) \oplus W(v, V) \oplus w$$$ between $$$V$$$ and $$$U$$$, and make $$$U$$$ the root of our new component.
This last step is the small to large optimization, to ensure the height of our trees is logarithmic.
With this data structure, we can maintain the number of connected components like in a usual dsu, and whenever an edge $$$(u, v)$$$ with weight $$$w$$$ is added, and $$$u$$$ and $$$v$$$ belong to the same component, we can obtain the value of $$$W(u, v)$$$ in $$$\mathcal{O(\log(n))}$$$, and check if it is equal to $$$w$$$.
This idea is similar to the data structure described here, and is useful in other contexts.
Complexity: $$$\mathcal{O}(\log(q + k)(n + m + k + q))$$$.
We have three different solutions for this problem, one of them found during the Olympiad! I'll let the contestant who found it post it if he wants to.
You can model a grid as a bipartite graph between rows and columns.
Whenever coding or designing a data structure, keep in mind all the invariants you are maintaining. I like to think of data structures as graphs with invariants or monovariants in each node. I have a blog draft on how to use this to design data structures, inspired by this. Maybe I will publish it.