I haven't seen anyone to write about this technique, so I decided to make a blog about it. I know that it is mostly general intuition, but not everyone really understand it. Also, I would be happy if you add something in comments or correct some errors. Also, before reading this blog I recommend to have some knowledge about segment tree and divide and conquer.
The main idea
When we have some divide and conquer algorithm, we can memorize each recursive call to be able to operate with it as data structure. For example, when we do merge sort, we can memorize how array looked after sorting on each call. Using this we can get merge sort tree. Also, if we memorize quick sort in such way, we will get wavelet tree. A lot of standart ways to use divide and conquer would lead to segment tree. But, it also can be used when we divide array on 3 parts or more, when we divide considering parity of indexes of array and so on. The main usage of it, that we can do almost all operation which we can do on segment tree (in fact it depends on the task that we are solving) and in the most cases it optimize solutions alot. For example, if we havee recursion that recursevily divide array on even and odd elements,
and assume we memorize each level (even and odd array on each time), then we can do lazy propogation here. For example, add $$$x$$$ to all elements on segment $$$[l,r]$$$ we can make in the same way as in the segment tree. But this recursion can also solve querries to add $$$x$$$ to all elemnts with even (or odd) indexes on segment $$$[l,r]$$$ or such indexes that are equal 3 by modulo 4 or in general any index that has last $$$k$$$ bits equal to some number. Also, as you may see, if we replace indexes by numbers, we would get classic binary trie (preffix tree).
The problem
We will solve this problem.
Solution
Firstly, we will solve problem without the querries. To make it easier, we can change vertex numbers on the tree using DFS.
For example, from this 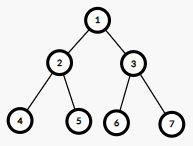 as in the statement to this
as in the statement to this 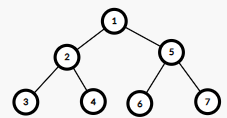 .
.
After changing graph indexing, we can use divide and conquer to check if permutation is good. In fact, for any vertex, all vertexes in it's subtree after sorting should be continuous. It is true because of the way we change vertex number. So, it can be easily checked by just taking maximum and minimum of all subtree and check if there are same number of elements between maximum and minimum as there is in the tree (It works because all elements are distinct). Important thing is that we can do it on segments, since segment [1,n] represent whole tree while segment [2, $$$\lfloor\frac{n+1}{2}\rfloor$$$ ] represent it's right subtree and segment [ $$$\lfloor\frac{n+1}{2}+1\rfloor$$$ ,n] represent left subtree. Also, it is important to check if depth of the vertex is the same. You see, in any DFS order, depth of all vertexes doesn't change, but it is easy to come up with test, where divide and conquer solution will give yes and depthes will be wrong.
This solution works in $$$O(n\cdot log(n))$$$, but we can memorize all layers of recursion call just like in the segment tree. In fact, all we need to memorize is maximum and minimum on segment and if segment is good (if check function from divide in conquer would return true or false). Then, we have querries which is to swap two elements. In fact, it is the same as change value of one element to the value of second and vice versa for the second element, so all we need to be able to do is to change value of some element. Here, we can just memorize all states of recursion and make something like segment tree, where segment [l,r) has children [l+1, $$$\lfloor\frac{l+r}{2}\rfloor$$$ ) and [ $$$\lfloor\frac{l+r}{2}\rfloor$$$ , r). So, it will work in $$$O(n\cdot log(n))$$$
Application
339D - Xenia and Bit Operations is a problem which shows this technique. It is literaly in the statement, what we need to memorize. Here is the code 148215700.






