Hello everyone,
I did like to give a brief overview of Fermat's theorem and its proof. There are various methods to prove Fermat's Little theorem, but I found the combinatorial approach to be the most straightforward and easy to understand. I'd like to discuss Fermat's theorem and its proof using combinatorics.
Fermat's Little Theorem
It states that if $$$p$$$ is a prime and $$$a$$$ is any integer not divisible by $$$p$$$, then $$$a^{p−1} − 1$$$ is divisible by $$$p$$$
Example:
Say a = 2 , p = 5.
$$$a^{p-1} $$$
$$$ = 2^{5-1}$$$
$$$ = 2^4 = 16$$$
$$$ \equiv 1 \pmod{5}$$$
Proof (Combinatorics Approach)
The concept behind this proof is to approach it through a combinatorial problem and discover its solution, which indirectly verifies the theorem. Let's explore this straightforward combinatorial problem.
Problem
Consider a Necklace chain consisting of beads. There are $$$p$$$ beads in this chain. You are allowed to color each bead with $$$a$$$ possible colors available. The colors are available in infinite amounts, there is no other restriction on coloring. Find the number of ways to color these beads.
It can be easily shown that there are $$$a^p$$$ ways to color the beads to get different necklaces. (considering cyclic rotations as distinct). Every bead has $$$a$$$ options to be colored.
Consider a small variation to this problem, Among all possible $$$a^p$$$ permutations, Let's try to group them based on similar cyclic rotations. Two permutations are said to be equivalent if any of them can be generated from the cyclic rotation of the other.
For example, consider $$$a = 2, p = 3$$$. Let X and Y be the 2 possible colors available. Let's try to group these $$$2^3 = 8$$$ strings (all permutations) based on similar cyclic rotations. We get:
- Group 1: XXX
- Group 2: YYY
- Group 3: XXY, XYX, YXX
- Group 4: XYY, YYX, YXY
Here we get 4 different groups of sizes 1,1,3,3 each. Let's try to analyze these group sizes in-depth.
Periodicity of a String:
The periodicity of a string refers to the smallest length of a substring that, when repeated, forms the entire string. In other words, it's the minimum length of a substring that can be repeated periodically to recreate the original string.
Example
- ABCABC has periodicity = 3 (ABC)
- ABABAB has periodicity = 2 (AB)
Claim 1
The periodicity of a string is the same as its group size of similar cyclic rotations.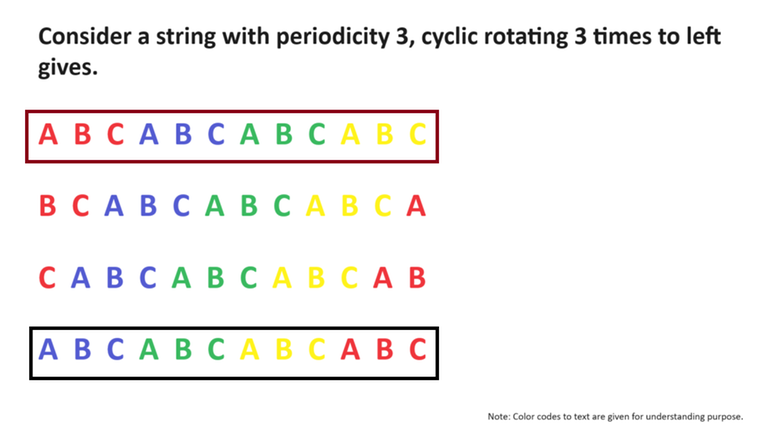
Claim 2
The periodicity of a string, as well as its group size, are factors of the string's total length.
From the above 2 claims, we can conclude that for the original problem (filling $$$p$$$ beads with $$$a$$$ colors) we get $$$a^p$$$ strings, and these strings have periodicity as $$$1$$$ or $$$p$$$. ($$$1$$$ and $$$p$$$ are the only factors of $$$p$$$ (prime)).
Example $$$a = 2, p = 3$$$
- Group 1: XXX Periodicity = 1
- Group 2: YYY Periodicity = 1
- Group 3: XXY, XYX, YXX Periodicity = 3
- Group 4: XYY, YYX, YXY Periodicity = 3
It can also be shown that among $$$a^p$$$ strings, there are only $$$a$$$ strings with periodicity as $$$1$$$. (Same color applied to all beads Example: Group 1: XXX, Group 2: YYY)
From the above statements we can conclude that the remaining strings $$$a^p - a$$$ have periodicity as $$$p$$$, which says that we can separate the remaining $$$a^p - a$$$ strings into groups of sizes $$$p$$$. This concludes that $$$a^p - a$$$ is a multiple of $$$p$$$. So
$$$a^p - a \equiv 0 \pmod{p}$$$
$$$a^p \equiv a \pmod{p}$$$
$$$a^{-1}*a^p \equiv a^{-1}*a \pmod{p}$$$
$$$a^{p-1} \equiv 1 \pmod{p}$$$
This completes the proof. My main motivation for exploring such proofs is the belief that visualizing a problem from different perspectives can simplify the process, making the proofs more intuitive and accessible, rather than relying solely on rigorous mathematical approaches.
References:
1) Wikepedia





