1779A - Зал славы
Author: n0sk1ll
1779B - Конструктив от MKnez
1779C - Наименьшая префиксная сумма
Author: n0sk1ll
1779D - Борис и его восхитительная прическа
Author: n0sk1ll
1779E - Параллельные показательные матчи Ани
Author: BULLMCHOW
- if $$$j<i$$$, then every character in the segment $$$s[j...i-1]$$$ must be greater than or equal to $$$s_i$$$;
- if $$$i<j$$$, then every character in the segment $$$s[i+1...j]$$$ must be smaller than or equal to $$$s_i$$$.
We want to reorder the string $$$s$$$ and get the string $$$s'$$$. Then, we check if we can delete some characters in $$$s'$$$ to achieve $$$t$$$. In other words, we want $$$t$$$ to be a subsequence of $$$s'$$$. Let us take a look at a general algorithm that checks if the string $$$a$$$ is a subsequence of the string $$$b$$$. We iterate through $$$a$$$ and for each character we find its first next appearance in $$$b$$$. If such character does not exist, we conclude that $$$a$$$ is not a subsequence of $$$b$$$. If we complete the iteration gracefully, then $$$a$$$ is a subsequence of $$$b$$$. We will try to check if $$$t$$$ is a subsequence of $$$s$$$, but with allowing ourselves to modify $$$s$$$ along the way.
We maintain $$$26$$$ queues for positions of each lowercase English letter in the string $$$s$$$. We iterate through the string $$$t$$$ and for every character $$$t_i$$$, we try to move the first such character in $$$s$$$ to position $$$i$$$. In other words, at every moment, the prefix of string $$$s$$$ is equal to the prefix of string $$$t$$$ (if it is possible). For the current character $$$t_i$$$ and the corresponding $$$s_j$$$, prefixes $$$t_1t_2\dots t_{i-1}$$$ and $$$s_1s_2\dots s_{i-1}$$$ are the same, which means that $$$j\geq i$$$. To move $$$s_j$$$ to position $$$i$$$, we need to delete all characters between $$$s_i$$$ and $$$s_j$$$ that are smaller than $$$s_j$$$. We will delete them and all characters from the current prefix $$$s_1s_2\dots s_{i-1}$$$ from the queues because they are no longer candidates for $$$s_j$$$. By doing so, $$$s_j$$$ will be the first character in the corresponding queue. If at some moment in our greedy algorithm, the queue we are looking for becomes empty, then the answer is "NO". Otherwise, we will make the prefix $$$s_1s_2\dots s_m$$$ equal to the $$$t$$$ and delete the remaining characters from $$$s$$$.
Why this greedy is optimal? Let's suppose for some character $$$t_{i_1}$$$ we chose $$$s_{j_1}$$$ and for $$$t_{i_2}$$$ we chose $$$s_{j_2}$$$, such that $$$i_1< i_2$$$, $$$j_1>j_2$$$ and $$$t_{i_1}=t_{i_2}=s_{j_1}=s_{j_2}$$$. We need to prove that if we can move $$$s_{j_1}$$$ to position $$$i_1$$$ and $$$t_{i_2}$$$ to position $$$i_2$$$, when we can move $$$s_{j_2}$$$ to $$$i_1$$$ and $$$s_{j_1}$$$ to $$$i_2$$$. In the moment when we chose $$$s_{j_1}$$$, prefixes $$$t_1t_2\dots t_{i_1-1}$$$ and $$$s_1s_2\dots s_{i_1-1}$$$ are the same, so $$$j_1\geq i_1$$$. Similarly, $$$j_2\geq i_2$$$, which means the only possibility is $$$i_1<i_2\leq j_2<j_1$$$.
If we can move $$$s_{j_1}$$$ to position $$$i_1$$$, than we can also move $$$s_{j_2}$$$ to $$$i_1$$$ because $$$s_{j_1}=s_{j_2}$$$ and $$$j_2<j_1$$$. Also, if we can move $$$s_{j_1}$$$ to $$$i_1$$$, than we can move $$$s_{j_1}$$$ to $$$i_2$$$ because $$$i_1<i_2$$$, from which it follows that we can move $$$s_{j_2}$$$ to $$$i_2$$$, because $$$s_{j_2}=s_{j_1}$$$ and $$$j_2<j_1$$$.
Overall complexity is $$$O(\alpha (n+m))$$$, where $$$\alpha$$$ is the alphabet size (\alpha=26 in this problem).
1779F - Ксолдовские камни
Author: n0sk1ll
For a matrix of type $$$1$$$, Misha can block all empty cells (except the one Vova stands on).
For a matrix of type $$$2$$$, Misha finds the shortest path to some exit with a single BFS and then blocks every other cell.
Matrices of type $$$3$$$ are more complicated. We want to find two shortest paths to the two closest exits and block the remaining empty cells.
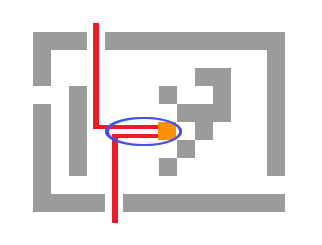
But, notice how the paths will likely share their beginnings. We do not have to count those cells twice. Let's take a look at the junction where the two paths merge. If we first fix the junction, finding the shortest path to Vova can be done by running a single BFS and precalculating the shortest distances from each cell to Vova. Finding the shortest path from the junction to the two closest exits can also be done with BFS and precalculation. We modify the BFS, making it multi-source, with a source in each exit. Also, we will allow each cell to be visited twice (but by different exits). We will need to maintain the following data for each cell:
- How many times was it visited;
- The last exit/source that visited it;
- The sum of paths from all exits/sources that visited the cell so far.
Running the BFS with proper implementation produces the answer. When everything said is precalculated, we fix the junction in $$$O(nm)$$$ ways (each empty cell can be a valid junction), and then calculate the shortest path from Vova to the two closest cells in $$$O(1)$$$ per junction.
Total complexity is $$$O(nm)$$$.