In one move, Milica can replace the whole string with $$$\texttt{AA} \ldots \texttt{A}$$$. In her second move, she can replace a prefix of length $$$k$$$ with $$$\texttt{BB} \ldots \texttt{B}$$$. The process takes no more than $$$2$$$ operations. The question remains — when can we do better?

In the hint section, we showed that the minimum number of operations is $$$0$$$, $$$1$$$, or $$$2$$$. We have $$$3$$$ cases:

1. No operations are needed if $$$s$$$ already contains $$$k$$$ characters $$$\texttt{B}$$$.

2. Else, we can use brute force to check if changing some prefix leads to $$$s$$$ having $$$k$$$ $$$\texttt{B}$$$s. If we find such a prefix, we print it as the answer, and use only one operation. There are $$$O(n)$$$ possibilities. implementing them takes $$$O(n)$$$ or $$$O(n^2)$$$ time.

3. Else, we use the two operations described in the hint section.

A fun fact is that only one operation is enough. Can you prove it?

Try a greedy approach. That is, split each $$$a_i$$$ only as many times as it should (and try to create almost equal parts).

We will iterate over the array from right to left. Then, as described in the hint section, we will split the current $$$a_i$$$ and create almost equal parts. For example, $$$5$$$ split into three parts forms the subarray $$$[1,2,2]$$$. Splitting $$$8$$$ into four parts forms the subarray $$$[2,2,2,2]$$$. Notice that the subarrays must be sorted. Because we want to perform as few splits as possible, the rightmost endpoint value should be as high as possible (as long as it is lower than or equal to the leftmost endpoint of the splitting of $$$a_{i+1}$$$ if it exists).

When we iterate over the array, it is enough to set the current $$$a_i$$$ to the leftmost endpoint of the splitting (the smallest current value). It will help to calculate the optimal splitting of $$$a_{i-1}$$$. For the current $$$a_i$$$, we want to find the least $$$k$$$ such that we can split $$$a_{i-1}$$$ into $$$k$$$ parts so the rightmost endpoint is less than or equal to $$$a_i$$$. More formally, we want $$$\lceil \frac{a_{i-1}}{k} \rceil \leq a_i$$$ to hold. Afterwards, we set $$$a_{i-1}$$$ to $$$\lfloor \frac{a_{i-1}}{k} \rfloor$$$ and continue with our algorithm. The simplest way to find the desired $$$k$$$ is to apply the following formula:

There are $$$q \leq 2\cdot 10^5$$$ queries: given an index $$$i$$$ and an integer $$$x>1$$$, set $$$a_i := \lceil \frac{a_i}{x} \rceil$$$. Modify the array and print the answer to the original problem. Please note that the queries stack.

The solution does not exist only for "small" $$$k$$$ or when $$$n+m-k$$$ is an odd integer. Try to find a construction otherwise.

Read the hint for the condition of the solution's existence. We present a single construction that solves the problem for each valid $$$k$$$.

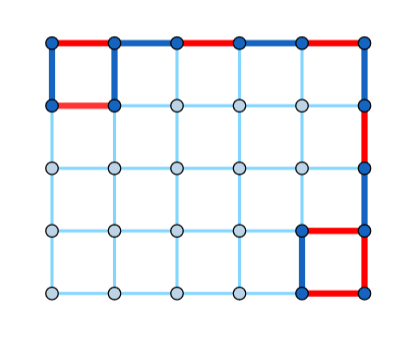
One can verify that the pattern holds in general.

How would you write a checker? That is, how would you check that a valid walk of length $$$k+1$$$ exists in the given grid (with all the edges colored beforehand)?

If $$$a_i > b_i$$$, swap them. Imagine the pairs $$$(a_i,b_i)$$$ as intervals. How can we visualize the problem?

The pair $$$(a_i,b_i)$$$ represents some interval, and $$$|a_i - b_i|$$$ is its length. Let us try to maximize the sum of the intervals' lengths. We present three cases of what a swap does to two arbitrary intervals.

Notice how the sum of the lengths increases only in the first case. We want the distance between the first interval's right endpoint and the second interval's left endpoint to be as large as possible. So we choose integers $$$i$$$ and $$$j$$$ such that $$$i \neq j$$$ and $$$a_j - b_i$$$ is maximized. We add twice the value, if it is positive, to the original absolute beauty. If the value is $$$0$$$ or negative, we simply do nothing.

To quickly find the maximum of $$$a_j - b_i$$$ over all $$$i$$$ and $$$j$$$, we simply find the maximum of $$$a_1,a_2,\ldots a_n$$$ and the minimum of $$$b_1,b_2, \ldots b_n$$$. Subtracting the two extremum values produces the desired result.

How to handle point queries?

To solve the problem for matrices of $$$3$$$-rd type, find the shortest path to $$$2$$$ closest exits with a modification of BFS. Block all cells not belonging to the path with obstacles.

For a matrix of type $$$1$$$, Misha can block all empty cells (except the one Vova stands on).

For a matrix of type $$$2$$$, Misha finds the shortest path to some exit with a single BFS and then blocks every other cell.

Matrices of type $$$3$$$ are more complicated. We want to find two shortest paths to the two closest exits and block the remaining empty cells.

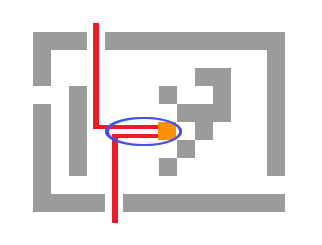
But, notice how the paths will likely share their beginnings. We do not have to count those cells twice. Let's take a look at the vertex where the two paths split. If we first fix the vertex, finding the shortest path to Vova can be done by running a single BFS and precalculating the shortest distances from each cell to Vova. Finding the shortest path from the vertex to the two closest exits can also be done with BFS and precalculation. We modify the BFS, making it multi-source, with a source in each exit. Also, we will allow each cell to be visited twice (but by different exits). We will need to maintain the following data for each cell:

• How many times was it visited;
• The last exit/source that visited it;
• The sum of paths from all exits/sources that visited the cell so far.

Running the BFS with proper implementation produces the answer. When everything said is precalculated, we fix the vertex in $$$O(nm)$$$ ways (each empty cell can be a valid vertex), and then calculate the shortest path from Vova to the two closest cells in $$$O(1)$$$ per vertex.

Total complexity is $$$O(nm)$$$.

What is the maximum number of cells that Misha can block so each initial exit is still reachable by Vova? Solve under the constraints $$$n, m \leq 500$$$.