Hi Codeforces! If you calculate midpoint like
int get_midpoint(int l, int r) {//[l, r)
int pow_2 = 1 << __lg(r-l);//bit_floor(unsigned(r-l));
return min(l + pow_2, r - pow_2/2);
}
then your segment tree requires only $$$2 \times n$$$ memory.
#include <bits/stdc++.h>
using namespace std;
int get_midpoint(int l, int r) {//[l, r)
int pow_2 = 1 << __lg(r-l);//bit_floor(unsigned(r-l));
return min(l + pow_2, r - pow_2/2);
}
int n;
set<int> internal_nodes, leaf_nodes;
map<int, int> depth_of_segments_not_pow2;
void build(int v, int l, int r) {//[l, r)
if(r-l == 1) {
const int depth_leaf = __lg(v), max_depth = __lg(2*n-1);
if(l == 0) {//left-most leaf
assert(v == int(bit_ceil(unsigned(n))));
assert(depth_leaf == max_depth);
}
assert(depth_leaf == max_depth || depth_leaf == max_depth - 1);
if((n&(n-1)) == 0) assert(depth_leaf == max_depth);
assert(n <= v && v < 2*n);
assert(!leaf_nodes.count(v));
leaf_nodes.insert(v);
return;
}
if(((r-l)&(r-l-1)) == 0) assert(get_midpoint(l,r) == (l+r)/2);
else depth_of_segments_not_pow2[__lg(v)]++;
assert(1 <= v && v < n);
assert(!internal_nodes.count(v));
internal_nodes.insert(v);
int m = get_midpoint(l, r);
build(2*v, l, m);
build(2*v+1, m, r);
}
int main() {
for(n = 1; n <= 520; n++) {
cout << "n: " << n << endl;
internal_nodes.clear();
leaf_nodes.clear();
depth_of_segments_not_pow2.clear();
build(1, 0, n);
assert(ssize(internal_nodes) == n-1);
assert(ssize(leaf_nodes) == n);
for(int i = 1; i < n; i++) assert(internal_nodes.count(i));
for(int i = n; i < 2*n; i++) assert(leaf_nodes.count(i));
//at most one "bad" segment per depth
//either left child or right child (or both) will have segment length
//a power of 2; then their subtrees are a perfect binary tree
for(auto [depth, cnt] : depth_of_segments_not_pow2) assert(cnt == 1);
assert(ssize(depth_of_segments_not_pow2) <= __lg(n));
}
return 0;
}
induction assumption: the segment tree with root segment $$$[0,n)$$$ turns into a complete binary tree which has $$$2 \times n - 1$$$ nodes and max depth = __lg(2*n-1).
observe:
0 = __lg(1)
1 = __lg(2) = __lg(3)
2 = __lg(4) = __lg(5) = __lg(6) = __lg(7)
...
so
__lg(v)= depth of node vmax depth of complete binary tree = depth of any node on lowest level
node
2*n-1is always on the lowest level
Also note: get_midpoint(l + x, r + x) = get_midpoint(l, r) + x so we can "shift" any segment $$$[l,r)$$$ to $$$[0,r-l)$$$ and the corresponding segment trees have the same structure, hint: min(a + x, b + x) = min(a, b) + x
Induction step
case 0: $$$r-l$$$ is a power of 2
get_midpoint(l,r) returns $$$\dfrac{r+l}{2}$$$, and we get a perfect binary tree (which is also complete).
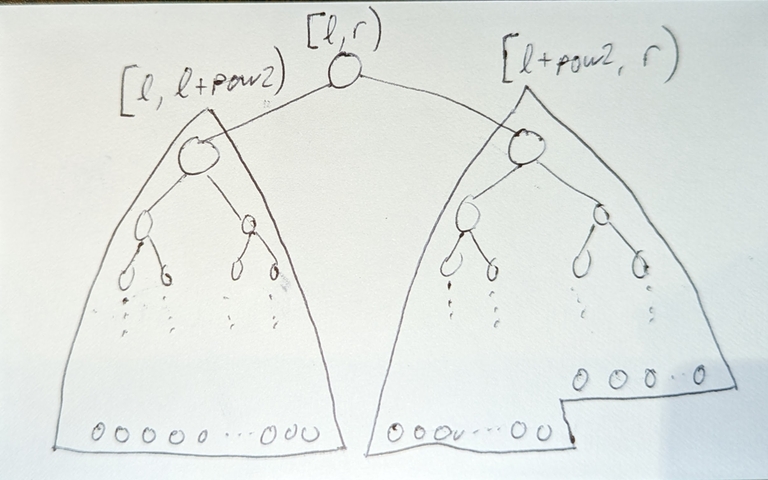
case 1: $$$l + pow2 < r - \frac{pow2}{2}$$$
$$$[l,r)$$$ splits into:
left child with segment $$$[l,l+pow2)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*pow2-1)right child with segment $$$[l+pow2, r)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*((r-l) - pow2)-1)
steps:
$$$ \frac{pow2}{2} < (r-l) - pow2$$$ (rearange case assumption)
$$$\frac{1}{2} \times (r-l) < pow2$$$ ($$$pow2$$$ is defined/calculated as: largest power of 2 $$$ \le (r-l)$$$ )
$$$(r-l) - pow2 < pow2$$$ (from step 2, multiply by 2, then subtract $$$pow2$$$)
$$$\frac{pow2}{2} < (r-l) - pow2 < pow2$$$ (combine steps 1,3)
$$$pow2 \le 2 \times ((r-l) - pow2) - 1 < 2 \times pow2-1$$$ (from step 4, multiply by 2, then subtract 1)
__lg(pow2)=__lg(2*((r-l) - pow2) - 1)=__lg(2*pow2-1)(from step 5, take log2; think about their binary representation)
From this, the left and right childs have the same max depth; the left child is a perfect binary tree; the right child is a complete binary tree, so overall it's a complete binary tree.
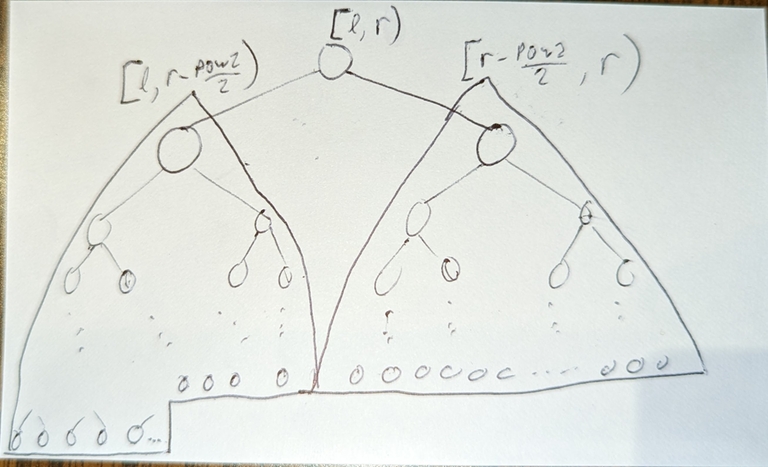
case 2: $$$l + pow2 \ge r - \frac{pow2}{2}$$$
$$$[l,r)$$$ splits into:
left child with segment $$$[l, r - \frac{pow2}{2})$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*((r-l) - pow2/2)-1)right child with segment $$$[r - \frac{pow2}{2}, r)$$$, (from induction assumption and "shift"-ing) a complete binary tree with max depth =
__lg(2*(pow2/2)-1)
steps:
$$$(r-l) - \frac{pow2}{2} \le pow2$$$ (rearange case assumption)
$$$pow2 < (r-l)$$$ ($$$pow2$$$ is defined/calculated as: largest power of $$$2 \le (r-l)$$$, see case 0 for when $$$(r-l)$$$ is a power of 2)
$$$\frac{pow2}{2} < (r-l) - \frac{pow2}{2}$$$ (from step 2, subtract $$$\frac{pow2}{2}$$$)
$$$\frac{pow2}{2} < (r-l) - \frac{pow2}{2} \le pow2$$$ (combine steps 1,3)
$$$pow2 \le 2 \times ((r-l) - \frac{pow2}{2}) - 1 \le 2 \times pow2-1$$$ (from step 4, multiply by 2, subtract 1)
__lg(pow2)=__lg(2*((r-l) - pow2/2) - 1)=__lg(2*pow2-1)(from step 5, take log2; think about their binary representation)__lg(2*((r-l) - pow2/2) - 1)=__lg(pow2)= 1 +__lg(pow2/2)= 1 +__lg(2*(pow2/2)-1)(from step 6, using log rules)
From this, the left child has max depth = 1 + right child max depth. The left child is a complete binary tree; the right child is a perfect binary tree, so overall, it's a complete binary tree.
I was inspired by ecnerwala's in_order_layout https://github.com/ecnerwala/cp-book/blob/master/src/seg_tree.hpp
I'll be waiting for some comment "It's well known in china since 2007" 😂






