| Codeforces Round 384 (Div. 2) |
|---|
| Закончено |
Владик заскучал по дороге домой и решил сыграть в следующую игру. Он взял n карт и положил их в ряд перед собой. На каждой карте Владика написано целое положительное число, не превосходящее 8. Он решил найти самую длинную подпоследовательность карт, для которой выполняются следующие условия:
- количество вхождений каждого числа от 1 до 8 в подпоследовательности отличается не более, чем на 1 от количества вхождений любого другого числа. Более формально, если в подпоследовательности ck карт с числом k на них, то для всех
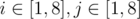 выполняется |ci - cj| ≤ 1.
выполняется |ci - cj| ≤ 1. - если в подпоследовательности имеется карта с числом x, то все карты с числом x должны составлять непрерывный отрезок в этой подпоследовательности (но не обязательно быть непрерывным отрезком в исходной последовательности). Например, последовательность карт [1, 1, 2, 2] удовлетворяет данному условию, а [1, 2, 2, 1] — нет. Обратите внимание, что [1, 1, 2, 2] не удовлетворяет первому условию.
Помогите Владику и найдите максимальную длину подходящей подпоследовательности.
В первой строке входных данных содержится число n (1 ≤ n ≤ 1000) — количество карт в последовательности Владика.
Во второй строке входных данных содержится n целых положительных чисел, не превосходящих 8 — описание последовательности Владика.
Выведите одно целое число — длину максимальной подпоследовательности, в которой выполняются все условия.
3
1 1 1
1
8
8 7 6 5 4 3 2 1
8
24
1 8 1 2 8 2 3 8 3 4 8 4 5 8 5 6 8 6 7 8 7 8 8 8
17
В первом примере числа на всех карточках равны, поэтому мы не сможем взять больше, чем одну карточку, поскольку нарушим первое условие.
| Название |
|---|




