| Codeforces Round 352 (Div. 1) |
|---|
| Закончено |
Сегодня в Кекляндии отмечают день переработки мусора. Чтобы отпраздновать это событие, Адил и Бера решили пойти в центральный парк подбирать валяющиеся на земле бутылки и доносить их до урны.
Центральный парк можно представить как координатную плоскость. На земле лежат n бутылок, i-я из которых находится в точке с координатами (xi, yi). И Адил, и Бера в каждый момент времени могут держать в руках не более одной бутылки каждый.
Процесс уборки для каждого из них выглядит следующим образом:
- Определиться, продолжать ли собирать мусор или остановиться.
- Если решено продолжить, то выбрать какую-нибудь ещё лежащую на земле бутылку и дойти до неё.
- Подобрать эту бутылку и дойти с ней до урны.
- Вернуться к шагу 1.
Адил и Бера могут передвигаться независимо. Они могут носить бутылки одновременно, каждую бутылку может подобрать любой их них, и один из них спокойно может стоять и смотреть, как другой собирает бутылки.
Они хотят так организовать процесс сборки бутылок, чтобы суммарное пройденное расстояние (то есть расстояние, пройденное Адилом, сложенное с расстоянием, пройденным Берой) было минимальным. Разумеется, при этом все бутылки должны оказаться в урне.
В первой строке входных данных записаны шесть целых чисел ax, ay, bx, by, tx и ty (0 ≤ ax, ay, bx, by, tx, ty ≤ 109) — изначальные координаты Адила, Беры и урны соответственно.
Во второй строке записано единственное целое число n (1 ≤ n ≤ 100 000) — количество бутылок, валяющихся на земле.
Далее следуют n строк, каждая из которых содержит два целых числа xi и yi (0 ≤ xi, yi ≤ 109) — координаты i-й бутылки.
Гарантируется, что изначально Адил, Бера, урна и все бутылки находятся в разных точках парка.
Выведите одно вещественное число — минимальное суммарное расстояние, которое придётся пройти Адилу и Бере, чтобы положить все бутылки в урну. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если 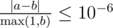 .
.
3 1 1 2 0 0
3
1 1
2 1
2 3
11.084259940083
5 0 4 2 2 0
5
5 2
3 0
5 5
3 5
3 3
33.121375178000
Рассмотрим первый пример.
Путь Адила: 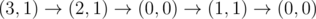 .
.
Путь Беры: 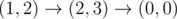 .
.
Длина пути Адила равняется 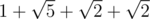 . Длина пути Беры равняется
. Длина пути Беры равняется 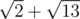 .
.
| Название |
|---|




