672A - Summer Camp
This one is a simple brute force problem, we will construct our array. Adding numbers between 1 and 370 will be enough. After construction we just have to print n-th element of array.
672B - Different is Good
We observe that in a good string all letters must be different, because all substrings in size 1 must be different. So if size of string is greater than 26 then answer must be - 1 since we only have 26 different letters.
Otherwise, Let's suppose we have k different letters in string sized n, in our string k elements must be stay as before, all others must be changed. So will be (n — k). Here is the code.
671A - Recycling Bottles
Let's solve the problem when Adil and Bera in the same coordinate with bin. Then answer will be 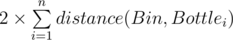 , let's say T to this value. If Adil will take i-th bottle and Bera will take j-th bottle (i ≠ j), then answer will be T + distance(Adil, Bottlei) - distance(Bin, Bottlei) + distance(Bera, Bottlej) - distance(Bin, Bottlej).
, let's say T to this value. If Adil will take i-th bottle and Bera will take j-th bottle (i ≠ j), then answer will be T + distance(Adil, Bottlei) - distance(Bin, Bottlei) + distance(Bera, Bottlej) - distance(Bin, Bottlej).
Because for all bottles but the chosen ones we have to add 2 * distance(bottle, bin).
For example if we choose a bottle i for Adil to take first then we have to add distance(Adil, Bottlei) + distance(Bottlei, Bin).
In defined T we already count 2 * distance(Bottlei, Bin) but we have to count distance(Adil, Bottlei) + distance(Bottlei, Bin) for i.
So we have to add distance(Adil, Bottlei)-distance(Bottlei, Bin) to T.
Because 2 * distance(Bin, Bottlei)+distance(Adil, Bottlei)-distance(Bin, Bottlei) is equal to distance(Adil, Bottlei)+distance(Bottlei, Bin).
Lets construct two arrays, ai will be distance(Adil, Bottlei) - distance(Bin, Bottlei), and bj will be distance(Bera, Bottlej) - distance(Bin, Bottlej).
We will choose i naively, after that we have to find minimum bj where j is not equal to i. This one easily be calculated with precalculations, let's find optimal opt1 for Bera, also we will find second optimal opt2 for Bera, if our chosen i is equal to opt1 then Bera will go opt2, otherwise he will go opt1.
Don't forget to cases that all bottles taken by Adil or Bera!
Here is the code.
671B - Robin Hood
We observe that we can apply operations separately this means first we will apply all increase operations, and after will apply all decrease operations, vice versa. We will use following algorithm.
We have to apply following operation k times, add one to minimum number in array. We will simply binary search over minimum value after applying k operation. Let's look how to check if minimum will be great or equal to p. If 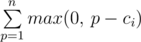 is less or equal to k then we can increase all elements to at least p. In this way we can find what will be minimum value after k operations.
is less or equal to k then we can increase all elements to at least p. In this way we can find what will be minimum value after k operations.
Let's say this minimum value to m. After we find it we will increase all numbers less than m to m. But there may be some operations we still didn't apply yet, this number can be at most n - 1, otherwise minimum would be greater than m because we can increase all numbers equal to m by one with this number of increases. Since minimum has to be same we just have to increase some elements in our array that equal to m.
We will use same algorithm for decreasing operations. Finally we will print max element — min element in final array. Overall complexity will be O(nlogk).
Here is the code.
Solution with another approach code.
671C - Ultimate Weirdness of an Array
If we calculate an array H where Hi is how many (l - r)s there are that f(l, r) ≤ i, then we can easily calculate the answer.
How to calculate array H. Let's keep a vector, vi keeps all elements indexes which contain i as a divisor — in sorted order. We will iterate over max element to 1. When we are iterating we will keep another array next, Let's suppose we are iterating over i, nextj will keep leftmost k where f(j, k) ≤ i. Sometimes there is no such k, then nextj will be n + 1. Hi will be equal to 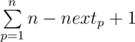 , because if we choose p as l, r must be at least nextp, so for l we can choose n-nextp+1 different r s.
, because if we choose p as l, r must be at least nextp, so for l we can choose n-nextp+1 different r s.
Let's look how we update next array when we iterate i to i - 1.
Let vi be b1, b2, b3...bk. Note that our l - r must be cover at least k - 1 of this indexes. l must less or equal to b2. So we have to maximize all nextp with n + 1 where p > b2. Otherwise If l ≥ b1 + 1 then r must be at least bk, that's we will maximize all nextp's where b1 < p ≤ b2 with bk. And finally for all nextp's where (1 ≤ p ≤ b1) we have to maximize them with bk - 1. Observe that next array will be monotonic - in non decreasing order - after all operations. So we can easily make our updates with a segment tree that can perform following operations:
- Returns rightmost index i where nexti is less than some k.
- Returns sum of all elements in next array.
- Can assign some k to all elements between some l and r.
If all update and queries performed in O(logn) then overall complexity will be O(nlogn), we can also apply all this operations with STL set in same complexity.
Code with set structure: link
Code with segment tree: link
671D - Roads in Yusland
I want to thank GlebsHP, i originally came up with another problem similar to it, GlebsHP suggested to use this one in stead of it.
Let's look for a optimal subset of paths, paths may intersect. To prevent from this let's change the problem litte bit. A worker can repair all nodes between ui and some k, where k is in the path between ui and vi with cost ci, also paths must not intersect. In this way we will never find better solution from original problem and we can express optimal subset in original problem without any path intersections in new problem.
Let's keep a dp array, dpi keeps minimum cost to cover all edges in subtree of node i, also the edge between i and parenti. How to find answer of some i. Let's choose a worker which uj is in the subtree of i and vj is a parent of node i. Then if we choose this worker answer must be cj + (dpk where k is child of a node in the path from uj to i for all k's). Of course we have to exclude nodes chosen as k and in the path from uj to i since we will cover them with j-th worker. We will construct a segment tree by dfs travel times so that for all nodes, workers which start his path in subtree of this node can be reached by looking a contiguous segment in tree. In node i, segment will keep values what will be dpi equal to if we choose this worker to cover path between uj and parenti. We will travel our tree with dfs, in each i after we calculated node i's children dp's we will update our segment in following way, add all workers to segment where uj = i with value cj + (sum of node i's children dp's). For all workers vj equal to i, we must delete it from segment, this is assigning inf to it. The only thing we didn't handle is what to do with workers under this node. Imagine all updates in subtree of node k where k is a child of node i. We have to increase all of them by (sum of node i's children dp's-dpk). After applying all of this operations answer will be minimum value of workers start their path from a node in subtree of i in segment tree.
Overall complexity will be ((n + m)logm).
Please look at the code to be more clear.
671E - Organizing a Race
Intended solution was 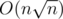 . Here is Zlobober's
. Here is Zlobober's 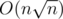 code: Link.
code: Link.
O(n2) Solution
Let cost(l, r) be minimum cost to make l-r suitable for a race. In task we have to find such l-r that cost(l, r) ≤ k and r-l+1 is maximum.
How to calculate cost(l, r): Let's look at how we do our increases to make race from l to r (first stage) possible. Greedily we will make our increases in right as much as possible. So if we run out of gas in road between i and i+1 we will add just enough gasoline to Gi. After make first stage possible we will add gasoline to r just enough to make second stage possible. This solution will be O(n3).
Let's find nexti, nexti will keep leftmost j that we can't reach with current gasoline, we will also keep needi that keeps how many liter gasoline we have to add to nexti-1. After applying this increase city nexti will be reachable from i, cars will be consumed all of their gasoline just before taking gasoline in city nexti.
How to find it: We will keep an array pre where prei = prei - 1 + Gi-Wi. If prej-prei - 1 < 0 then we can't reach to j + 1. If we find leftmost j (j ≥ i) where prej is strictly smaller than prei then nexti will be equal to j and needi will be equal to prej-prei - 1.
Building tree: Let's make a tree where nexti is father of node i. In dfs travel, when we are in a node i all increases will be made to make all first stages possible from i to all j's, now we will keep an array suff where suffi = suffi - 1 + Gi-Wi - 1. So when we are increasing a city u's Gu we have to increase all suff values from u to n. We will also keep another array cost, costj will keep the cost to make stage 1 possible from i to j+1. Increases will be nearly same, for u we will increase all v's costs v ≥ u. So when we reach a node i we will apply increases to make first stage possible between i ans nexti. When we are done with this node, we will revert increases.
Last part: Now we have to find rightmost j for all i's. Let's look at whether it is possible or not for a j. We can check it in O(1). First costj - 1 must be less or equal to k, also maximum(suffk i ≤ k < j)-(suffj-deltaj) + (costj-deltaj) ≤ k. deltaj keeps how many increases we apply to node j. We will decrease them since direct increases in j are made for j+1, we don't need to keep delta array since it will not effect expression. Also observe that the only thing changes in expression is maximum(suffk i ≤ k < j). In this way problem can be solved in O(n2). Both sqrt dec. solutions are using the same idea. Main solution will be posted soon.
How to Reduce it to O(nlog2n)
Let pi be costi-suffi. As we said before this value will never change.
Let's keep a segment tree. In each node we will keep such values. Assume this node of segment covers between l and r. We will keep such ind1, ind2 and mxsuff.
ind1 will keep minimum pj's index where l ≤ j ≤ r.
ind2 will keep minimum (maximum{suffl≤ k < j}+pj)'s index where mid + 1 ≤ j ≤ r this means we have to choose j from this nodes right child.
mxsuff will keep maximum{suffl≤k≤r}.
We also have to keep values for ind1 and ind2 (pind1 and (maximum{suffl≤ k < ind2}+pind2)).
How to update them: In a update we will increase some some suffixes costi and suffi values. So ind1 will be same for each node. For every covered node mxsuff will increase by k (k is increase value in update). Tricky part is how to update ind2. Let's define a function relax(). relax(u) calculates ind2 value for node u. Note that for relax function to work all nodes in subtree of u must be calculated already. We will call relax function after calculating this nodes children. We will come to relax function later.
How to query: We can use pretty much same function as relax. We have to query find values for a l-r segment. We will keep an extra value in function, let's call it t. If this node covers segment a-b then t will keep maximum{suffl≤ k < a}}. If this node doesn't intersect with l-r segment we will return worst values (for example for mx_suff value we will return -inf). Let's look what to do when this node is covered by l-r. If mxsuff value of this node's left child is greater or equal to t then ind2 value will be same. So if maximum{suffl≤ k < ind2}+pind2) is lower or equal to k for this node answer is ind2, it is greater than k then we will go this nodes left child to calculate answer. If mxsuff value of this node's left child is lower than t value then (maximum{suffl≤ j < mid}) will equal to t for each j. So we just have to rightmost j that pj ≤ k - t in subtree of this node. This can be calculated in O(logn) time. We didn't look at right child yet, so we will go to right child again with same t value. What to do when this node intersects with l-r and l-r doesn't cover it. We will go both children, first to left, after we will update t value for right child by mxsuff value returned from left child. We will lazy prop to push values.
Other condition: In node l we have to query between l and r, r is rightmost index that costr - 1 < k. Since cost values are monotonic this r can be found easily in O(logn).
Relax function can be calculated nearly same as query. But this will work in O(logn), since we just have to go exactly one child, since we don't interested in rightmost values.











Solved D div2 (B div1) in O(n log n) due to sorting.
first sort the array , get the prefix you'll add the K to by iterating on prefixes, to make the prefix numbers reach the next number in the array you need a K if this Newk >= k , break , calculate minimum by taking the prefix sum adding k then taking the average.
simply find the maximum doing the same operations on suffixes, then print difference .
Surprisingly I did something similar but my implementation failed test #10
What could the problem be?
Submission
prefix_sum array for coins needed to raise above a certain level and likewise, a suffix_sum array for coins that need to be spent to descend to a certain level
Using 2 binary searches and printing the difference
Kekoland is very good name for recycling :D
Can anyone explain DIV 2 C?
Can you tell me which part you didn't understand so i can explain it better. Cool pp btw.
Plz tell why did you choose this specific condition that distance(bera,bottle)-distance(bin,bottle) has to be minimized.. Thanks in advance...
For all bottles but chosen ones we have to add 2 * distance(bottle, bin).
If we choose a bottle i for Bera to take first then we have to add distance(Bera, Bottlei) + distance(Bottlei, Bin).
In defined T we already count 2 * distance(Bottlei, Bin) but we have to count distance(Bera, Bottlei) + distance(Bottlei, Bin) for i.
So we have to add distance(Bera, Bottlei)-distance(Bottlei, Bin) to T, because 2 * distance(Bin, Bottlei)+distance(Bera, Bottlei)-distance(Bin, Bottlei) is equal to distance(Bera, Bottlei)+distance(Bottlei, Bin).
what do pre and suf stand for in the code?
In stead of finding opt1 and opt2 you can do this. We have to find minimum b[j] where j != i right. pre[j] will be minimum over all b[1...j] and suff[j] will be minimum over all b[j...n]. Then if we look pre[i-1] and suff[i+1] we can find the minimum value.
Very nice problem! Also, I find the implementation of the solution very clever! :)
Thanks.But is DP solution easier than Greedy? for this problem.
Yes, i agree with that.
how is this dp solution? could you give some hints?
dp[i][j][k]whereiis the bottle number,jis bool if Bin pick a bottle or not andkis a bool if Bera pick a bottle or not.and on each step you have 3 options:
dp[i+1][j][k]and add 2*dis from t to bottle idp[i+1][1][k]and add dis from t to bottle i + dis from Bin to bottle i (only if j was == 0 )dp[i+1][j][1]and add dis from t to bottle i + dis from Bera to bottle i (only if k was == 0 )do not forget to check if j or k is 1 as a base condition when you reach i = n
and this is my code 17866824 for more clarification.
Simple && clear! Anyway, what is the maximum depth for this recursion? isn't
n? And, what does this line actually do :if(ret==ret)return ret;?yes, the maximum depth is
nand this line check if the value of the current state is previously calculated and if so return this value. when you use the
memset(dp,-1,sizeof dp);with type double, the values will not be -1 as expected but will benanwhich mean not a number, so ifnan == nanwill return false, but if the value not ananwill become true and return this value.so there will be four cases right in greedy meathod.
1.If all bottles are taken by ADIL. 2.If all bottles are taken by BREA. 3.If first bottle taken by ADIL and second my BERA 4.Viceversa of 3rd.
Is it?
Yes, pretty much like this.
I have one doubt. lets use the term profit. Suppose adil and bera approach the same bottle as the profit is same. Now one option is to let adil pick that bottle and bera chooses his next best option, if any. else beera just stands still and adil picks all the bottles. Or let beera pick the bottle and adil chooses his next best option. Will there be a case where letting one of them do so will affect the answer? Because ive been reading the submitted codes and im not getting where have they handled such a case. Suppose both are saving a dist of 5 by approaching a bottle r. If adil approaches r, beera's next best option is profit p. If beera approaches r, adils next best option is q. profit(r)<profit(p) & profit(r)<profit(q). But which of them chooses bottle r will be decided by profit(p)>profit(q) or profit(q)>profit(p). Can you please explain this scenario.
muratt What is test case 41? I tried different approaches. But one of them gets accepted while all the other 3 get WA on 41. What case is it? 671A - Recycling Bottles 18238071 Accepted 18238086 WA 41 18238187 WA 41 18238196 WA 41 18238214 WA 41
can you help as to why this case fails? im only changing the size of the profit variable from DBL_MAX to 0. or im changing the whole approach from computing negative profit to positive profit.
See http://forums.codeguru.com/showthread.php?469185-DBL_MIN-is-not-less-than-zero
Solved div1 C in O(nlogn + sum(cntdivisors(ai))).
Let's prefi — weirdness of the array [a1, a2, .., ai] and sufi — weirdness of the array [ai, ai + 1, .., an].
Let's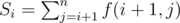 . How to calculate S. We will iterate i over 1 to n. Let's bj = max(gcd(aj, ak)) where 1 ≤ k ≤ i and maxbj = max(bk)(j ≤ k ≤ n). Then
. How to calculate S. We will iterate i over 1 to n. Let's bj = max(gcd(aj, ak)) where 1 ≤ k ≤ i and maxbj = max(bk)(j ≤ k ≤ n). Then 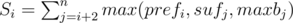 . When we are iterating we keep another array X, where Xj = max(prefi, sufj, maxbj).Notice that Xj ≥ Xj + 1.
. When we are iterating we keep another array X, where Xj = max(prefi, sufj, maxbj).Notice that Xj ≥ Xj + 1.
Let's look how we update array X when we iterate i - 1 to i. For each d divisor of ai we must assign Xk = max(Xk, d) for each 1 ≤ k ≤ lastd, where lastd rightmost index such that a[lastd] divisible by d. And we must assign Xk = max(Xk, prefi). Notice that if there are k < i, such that ak divisible by d, then array X does not change. So we consider each d just one time. So we can easily make our updates with a segment tree that can perform following operations:
- Returns rightmost index i where Xi is greater than or equal some k.
- Returns sum of all elements in X array between some l and r.
- Can assign some k to all elements between some l and r.
Here is the code.
can anyone explain D div2 a bit more with examples? its editorial is not clear for me.
Is there's a closed formula for div2 A or better algorithm for bigger constraints ?
1 to 9 gives you 9 digits
10 to 99 gives you (99 — 10 + 1) * 2 = 180 digits
100 to 999 gives you 2700 digits
etc
So in one operation you could determinate range where N will belong. After that you could find in one operation exact number and in one more operation exact digit. O(1).
Tags please!
Did anyone mention that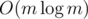 ?
?
Ultimate Weirdness of an Arraycan be solved inCan anyone please help me with my submission 17875045 for problem div2C? I don't understand where and why a precision error happens in my code. Thanks.
Can someone plz check my code, i am not able to figure out the error. (I have handled case for n=1, and either of them taking all the bottles is also handled. )
My Approach: First cal 2 * d(bin, bottle)
Second: Let Person A go first and greedily choose the bottle such that d(bin, bottle) — d(A,bottle) is max, then let B do the same, and take care of clash... Let this case denote I
Third: Same thing as first but this time with B going first. This case II
Fourth: Subtract the optimal case(max of both) from pre-computed distance
My Code: http://codeforces.me/contest/672/submission/17865445
What happens if nearest point is the same for both person A and person B? It seems that you don't consider this case therefore subtracting the same point distance expression twice.
edit: my bad, you do it
Thanks for such an awesome Contest!
Can anyone help in problem DIV 2 D / DIV 1 B? Since the editorial is not quite clear to me.
Couldn't find out binary search in code for task D -- Robin Hood
Now, I added two solutions, one with binary search, one with sort.
I didn't understand how we can perform the two operations in Div 1 B separately. How can you prove this?I have the exact same doubt.
How can we perform add operations first , possibly increasing the maximum value of the array to a new maximum and then perform the decrease operations independently?
inc(a) : increase by 1 the smallest element in array a and return the new array dec(a) : decrease by 1 the greatest element in array a and return the new array. It's easy to prove following equation inc((dec(a)) = dec(inc(a)) (1)
use (1) for many times, we can prove inc(dec.....(inc(dec(a)))) = inc(inc.....(dec(dec(a))))
sorry for my poor English
This part is not clear to me.
Would be nice to get more details on this from author or anyone else. Thanks in advance.
Roads in Yusland can be converted in to set cover problem which is NP- complete, right?
Yes. But this doesn't prove that "Roads in Yusland" is NP-hard. For that you would need the opposite reduction, that is, to convert "set cover" into "Roads in Yusland".
Thanks for clarifying that, but I've never understood why it is that way and not the other way round. Can you explain that?
Let's say it in an intuitive way. Suppose that you would have a polynomial time transformation T from "set cover" into "roads in yusland" that preserves the answer (a reduction), that is, given a valid input I of "set cover", T(I) is a valid input of "roads in yusland", and moreover: I has afirmative answer in "set cover" if and only if T(I) has afirmative answer in "roads in yusland". Since we know how to solve "roads in yusland" in polynomial time (in fact nlogn according to the editorial of this problem), the existence of the transformation T would prove that "set cover" can be solved in polynomial time, as any input I of set cover can be transformed into T(I) and we can run the polynomial time algorithm above.
No one knows how to solve "set cover" (and many other problems equivalent under reduction) in polynomial time. When you reduce a problem P1 to a problem P2 (usually written P1<=P2), intuitively, you are saying that P1 is at most as difficult as P2, as a polynomial time algorithm for P2 gives you a polynomial time algorithm for P1. Usually, one reduces a difficult problem P1 to another problem P2 to prove that P2 is also difficult. You can interpret difficult as "no one knows how to solve it in polynomial time", but this is just intuitive. Perhaps this is not the place to be more precise.
For the opposite direction, if you reduce "roads in yusland" to "set cover" you are just saying that "roads in yusland" is easier than "set cover". But this does not give us anything new, as "roads in yusland" can be solved in nlogn, whereas "set cover" is not known to be in PTIME.
DP solution link for div2 C.If you have any doubt you could ping me.
http://codeforces.me/contest/672/submission/17885210
Another simple and efficient solution (O(1) extra space) has been submitted by andrew.volchek during the contest and can be found here.
DIV II Summer Camp Problem. O(1);
My Sol. http://ideone.com/fork/QCGsxB
Even easier and funnier is to force your younger brother to fill in the numbers while you're solving other problems.
Thanks for the suggestion dude.
For Div2 D/Div1 B we can make an (IMHO) easy solution which just emulates the process. For this reason we first sort the numbers, group together equal numbers using map. After this, we repeat the following process untill k is above 0: We consider the minimum amount of steps to either increase amount of money of all poorest people to the amount of the next poorest people and the days needed to make amount of richest equal to the amount of second richest. Let this number be minfill. It is easy to see that if (minfill < k), then answer is difference of current richest — current poorest. Otherwise, we calculate how the richest and the poorest will change, because only those numbers can change. At the end we set k = k — minfill and repeat the process. We are left with two corner cases — when the difference between poorest and richest is at most 1(in this situation nothing will ever change) and the case when we have only two groups (richest and poorest). We can then take their average coins and set the minfill to the number of steps needed to make all poorest/richest to the average.
Here is a link to my submission: http://codeforces.me/contest/672/submission/17870778
I solved problem E in time.
time.
17897954.
It would be awesome if you describe your solution in few words. Also as i now there is a O(nlogn) solution too.
OK.
The first part is the same as the intended solution. But I didn't use sqrt dec to maintain the sequence, instead I used a segment tree. We want to know the biggest value of maxi ≤ k < jsufk - sufj + costj. First it's easy to see that sufj - costj never changes.
OK, the next part is the most important. Construct a segment tree. Consider the interval [l, r], we maintain maxv representing maxl ≤ k ≤ rsufk and maxp representing maxl ≤ k ≤ rsufk - costk(which in fact never changes), and for it's right child(interval [mid, r]), we maintain mind representing the maximal value of maxl ≤ k < jsufk - sufj + costj for j [mid, r].
[mid, r].
Consider such a problem: for a interval [l, r] in the segment tree, we know that before the interval the maximal value of sufk is maxsuf, and we want to know j [mid, r] such that max{maxsuf, maxl ≤ k < jsufk} - sufj + costj is minimal. For the left child(interval [l, mid]), if it's maxv is bigger than maxsuf, then for the right child, the answer is exactly mind; otherwise, for the left child, the answer is the difference of maxsuf and it's maxp. So we only need to consider one of it's children. The full procedure can be done in
[mid, r] such that max{maxsuf, maxl ≤ k < jsufk} - sufj + costj is minimal. For the left child(interval [l, mid]), if it's maxv is bigger than maxsuf, then for the right child, the answer is exactly mind; otherwise, for the left child, the answer is the difference of maxsuf and it's maxp. So we only need to consider one of it's children. The full procedure can be done in  . Moreover, in this way, mind can also be maintained, and it's easy to solve the original problem in
. Moreover, in this way, mind can also be maintained, and it's easy to solve the original problem in  time.
time.
BTW, this is called Li Chao's tree in China, named after chnlich.
In addition, can you describe the solution?
solution?
Array S is unchanged suff array. We will build n segment trees, i-th of them will keep maximum(suffk i ≤ k < j)-Sj for each j. We will use persistent segment trees for building this n tree, we will iterate n to 1. Now when we are travelling our tree we will use another segment tree (let's call it T) to find rightmost r that satisfy our conditions. In each node x, this segment also will keep maximum(suffk x ≤ k < j)-Sj values for each j. When we travel from node x to y, we have to update our segment, maximum(suffk x ≤ k < j) will equal to maximum(suffl, y < = l < x) for a prefix (from x to a z z >= x-1) after adding y-(x-1) segment to our tree. How can we handle between y-(x-1), we will use persistent tree we built in the very beginning, in T segment we will keep a index, that will keep which node in persistent trees equals to this node (we will use lazy here) We will assign some node's lazy values some nodes from persistent trees. How to do increasing operation. Increasing a suffix l - n with some k means increasing a suffix's max values with k. So we will just increase some suffixes max values (lazy is required here too). To find rightmost r we have to keep minimum maximum(suffk i ≤ k < j)-Sj values in this nodes subtree. We will query some segment l-r each time. L is our node, and r is rightmost r that costr - 1 <= k.
I know explanation sucks too as much as solution. There is another solution with linear memory, GlebsHP and Zlobober came up with this one but as they say it is an overkill solution so i dont know this one.
I don't understand why we select i naively in the Recycling bottles problem. Can anyone help please?
Actually we dont need to, i think it just make implementation easier.
For Div 2E, Div1C, in the official code, I found these lines
FOR(i, 1, N - 1) for(int j = i; j < N; j += i) foreach(it, H[j]) v[i].pb(*it);I agree that the first two loops are O(nlogn), but after adding the foreach, why the total time complexity is still O(nlogn) overall. I think it should be O(n(logn)^2) or something.I now this is weird way to implement it but this for works at most 1 time since all numbers are distinct :p
.
Can somebody help me understand the (Div2 D -Robin Hood)'s editorial's first line
we can apply operations separately this means first we will apply all increase operations, and after will apply all decrease operations, vice versaInstead of doing "subtract 1 from the max, add 1 to the min" operation k times, you can do "add 1 to the min" k times on the original array and then "subtract 1 from the max" k times on the same array (or vice versa).
Notice that when you perform the first type of operation (addition of 1s), it doesn't matter if current max in the array allows you to do that or if you created a new max in the process because you will perform subtractions later on that will fix this. You can think of it this way: say sumOrg = sum of numbers in the original array. After all additions the sum is sumOrg + k and after subtractions it's sumOrg again, i.e., the sum of coins ultimately doesn't change, only some of the coins move from one person to another.
The editorial of Div2 D isn't clear, so i'm writing it in my words(may be you can understand) .
See this beautiful implementation by TooSimpIe to understand it completely :- [submission:http://codeforces.me/contest/671/submission/17855052] Hope it was helpful :)
It is VERY easy to understand
https://ideone.com/bjt3KI It is solution for div2 c. It works on ms visual c++, but it doesn
t work on gnu c++. Whats wrong with it?Problem E can be solved by heavy_light decompositon, we can divide the tree into heavy_light edges,and for every consecutive heavy_edge blocks, we can find the minimum suffix value,and maximum prefix value,this can be done in O(n) time. and for each query node, there are only log(n) blocks from this node to root,scan the block and find minimum suffix value and maximum prefix value, if min_suffix+max_prefix>=-k, then continue go right, else go left.
so this solution is O(n*log(n)
gosh, problem E passed
In editorial for DIV1C "Ultimate weirdness of an array" :
"Note that our l - r must be cover at least k - 1 of this indexes." — Why? It is not clear to me. Can anyone explain please?
Because otherwise there will be at least 2 elements in array that contain i as a divisor. So max gcd will be at least i.
Thanks.
i do not understand meaning of this sentence, can you please explain what does cover mean in this context? Thx
upd: got it, only after commenting. was stuck for 2 days!!
I was trying to solve D div2 (B div1) in O(n log n) by sorting the a[] array but I got TLE. http://codeforces.me/contest/671/submission/18344467
I look at the solution/editorial code and implement the same in Java 8 and I got TLE also
http://codeforces.me/contest/671/submission/18379904, my code logic is the same as solution https://ideone.com/cc3KO5 above... I think this solution use n*log(k) that is slower than n*log(n)
Is it unfair for Java developer that the code run so slow? Should I switch to C++? :(
Thanks!
Time limit is decided as 2 times of tester's Java code and 3 time of tester's C++ code. I dont know java but problem may be reading huge input. Also there are some Java codes works around 300 ms.
In 671B — Robin Hood, i don't know whats happening but the code provided in the tutorial is opening, a message "syntax error" is appearing on the screen that all, can any one help me with that?
C: https://ideone.com/lUIJyo так лучше
I love you.
I love you, too.
Div 2 B can be solved way easily 78841349