| Codeforces Round 324 (Div. 2) |
|---|
| Закончено |
Коля любит рассаживать гномов по кругу и раздавать им монеты, а Таня любит изучать тройки гномов, сидящих в вершинах равностороннего треугольника.
Более формально, в круге сидят 3n гномов. У каждого гнома может быть от 1 до 3 монет. Пронумеруем места в порядке следования по кругу числами от 0 до 3n - 1, пусть у гнома, сидящего на i месте, ai монет. Тогда если существует целое число i (0 ≤ i < n) такое, что ai + ai + n + ai + 2n ≠ 6, то Таня остается довольна.
Посчитайте количество способов выбрать ai так, чтобы Таня осталась довольна. Так как способов раздачи монет может быть много, вычислите остаток от их деления на 109 + 7. Два способа a и b считаются различными, если существует индекс i (0 ≤ i < 3n) такой, что ai ≠ bi (то есть, какой-то гном получил разное количество монет в этих двух способах).
В единственной строке записано число n (1 ≤ n ≤ 105) — треть количества гномов.
Выведите единственное число — остаток от деления количества вариантов раздачи монет, устраивающих Таню на 109 + 7.
1
20
2
680
20 способов для для n = 1 (наверху каждого треугольника сидит гном с индексом 0, в правой нижней вершине - с индексом 1, в левой нижней - с индексом 2): 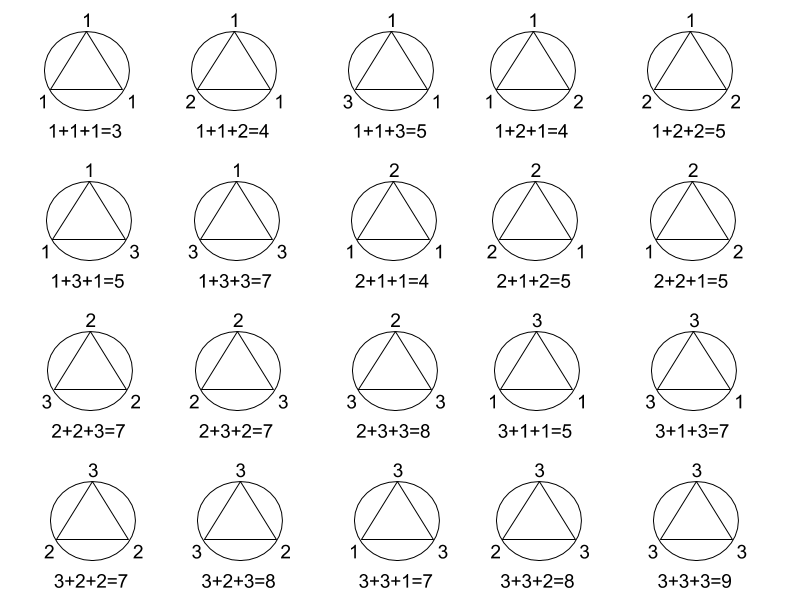
| Название |
|---|




