Two cases: t = 10 and t ≠ 10.
If t = 10 then there are two cases again :). If n = 1 then answer is - 1 (because there is not any digit divisible by t). If n > 1, then answer, for example, is '1111...110' (contains n - 1 ones).
If t < 10 then answer, for example, is 'tttttttt' (it, obviously, divisible by t).
The number of ways to choose ai (without any conditions) — 33n. Let A be the number of ways to choose ai with condition that in every triangle gnomes have 6 coins. Then answer is 33n - A.
Note that we can separate all gnomes on n independent triangles (i-th triangle contains of ai, ai + n, ai + 2n, i < n). So we can count answer for one triangle and then multiply the results. To count answer for one triangle, we can note that there are 7 ways to choose gnomes with 6 coins (all permutations 1, 2, 3 and 2, 2, 2).
So answer is — 33n - 7n. We count it in O(n).
Let's find a string that will be equal to s1 in k = n - t positions and equal to s2 in k = n - t positions. Let's denote q = quantity of i that s1i = s2i. If k ≤ q, then let's take k positions such that s1pos = s2pos and put in answer the same symbols. Then put in other n - k positions symbols, which are not equal to corresponding in s1 and s2 (we can do it, because we have 26 letters).
Now k > q. So, if there is an answer, where exists pos such that s1pos = s2pos, s1pos ≠ anspos, let's denote ansi = s1i, and then in any position such that s1i ≠ s2i = ansi and s1i = ansi (and in the same position in s2) we will choose ai, such that ai ≠ s1i and ai ≠ s2i (we can do it because k > q). So, for every position from q we can put symbols, equal to corresponding symbols in s1 and s2. Now we have strings s1, s2 of length n - q (such that s1i ≠ s2i for every i) and we should find string ans such that f(ans, s1) = f(ans, s2). We know that s1i ≠ s2i, so ansi may be equal to corresponding in s1 or to corresponding in s2 or not equal to s1i and to s2i. So, we need, at least, 2(k - q) symbols in answer to make f(s1, ans) = k - q and f(s2, ans) = k - q. Consequently, if n - q < 2(k - q), the answer is - 1, and else just put first k - q symbols in answer from s1, next k - q symbols from s2, and others won't be equal to corresponding in s1 and s2.
Solution works in O(n).
There is a fact that the distance between adjacent prime numbers isn't big. For n = 109 maximal distanse is 282. So let's find maximal prime p, such that p < n - 1 (we can just decrease n while it's not prime(we can check it in 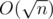 )). We know that n - p < 300. Now we have even (because n and p are odd) number n - p and we should divide it into a sum of two primes. As n - p < 300, we can just iterate over small primes P and check if P is prime and n - p - P is prime. You can check that there is a solution for all even numbers less than 300 by bruteforce.
)). We know that n - p < 300. Now we have even (because n and p are odd) number n - p and we should divide it into a sum of two primes. As n - p < 300, we can just iterate over small primes P and check if P is prime and n - p - P is prime. You can check that there is a solution for all even numbers less than 300 by bruteforce.
We can consider that we pay 2|i - j| coins for swap (we can divide answer in the end). Then we can consider that we pay |i - j| coins for moving pi and |i - j| for moving pj. So, if x was on position i and then came to position j, then we will pay at least |i - j| coins. Then the answer is at least 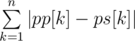 (pp — position k in permutation p, and ps — position k in permutation s). Let's prove that this is the answer by showing the algorithm of making swaps.
(pp — position k in permutation p, and ps — position k in permutation s). Let's prove that this is the answer by showing the algorithm of making swaps.
Let's consider that permutation s is sorted (our task is equal to it). Then we will put numbers from n to 1 on their positions.
How we can put n on its position? Denote ppos = n. Let's prove that there exists a position pos2 such that pos < pos2 and ppos2 ≤ pos(then we will swap ppos2 with n (and both numbers will move to their final positions and n will move to the right, so we can repeat this process until n returns to its position)). We can note that there are only n - pos positions that are bigger than pos. And how many numbers on these positions can be bigger than pos? We can say that answer is n - pos, but it's incorrect, because n is bigger than pos, but posn ≤ pos. Now we can use Pigeonhole principle and say that position x, such that x > pos and px ≤ pos exists.
But now our algorithm is O(n3). How we can put n in its position in O(n) operations? Let's move the pointer to the right while number is bigger than pos. Then swap n with found number. After we can move pointer from new n's position, so pointer always moves to the right and will not do more then n steps.










Problem D is clone of Timus #1356 ? But task C is more difficult than D . . .
Thanks for the awesome round! :)
BTW, there is a typo in Problem D's description:
"More formally, you are given an odd numer n." ->
"More formally, you are given an odd number n."
Whats proof for greedy method used for problem D ?
http://sweet.ua.pt/tos/goldbach.html
If we modify the 584C - Marina and Vasya to find
but not
, what is the fast solution to the new problem?
For example, "aaabbc" is different from "bbcaad" in exactly 1 characters in the new "difference rule" because one permutation of "bbcaad" is "aadbbc". The difference between s1 and s2 in the new problem may be calculated like this:
And it seemed that we can use the character c with minimal cnt[c] to "provide difference" firstly if we want to build a second string.
Didn't the question tell us to find a third string different from them in exactly t characters (irrespective of positions) i.e. your modified version?
Please correct me if I am making some mistake.
So I wasn't the only one with the same confusion. Here is what the author wanted to mean:
If am not wrong, the difference in problem C was based on the characters at the same positions. The difference in my modified version is based on the count of each character irrespective of positions. If what you said is about the modified version, I think you are correct.
where's the proof of correctness for Problem D ?
Goldbach's Conjecture
also Goldbach's_weak_conjecture
I have a questions considering problem E. 1. Why is the problem of transforming permutation p to s equal to problem of transforming permutation p to (1,2,...,n)? 2. Shouldn't it be "Let's move the pointer to the right until number becomes lower or equal to pos."
Interesting 584E. While I keep getting TLE for printing output with std::cout, the same test case could be finished in <200ms by printf...
Are there any method to significantly speed up std::cout?
ios_base::sync_with_stdio(false);cin.tie(0);I can't find C like difficult problem, more like hard to implement problem.
Actually, I think that it becomes somewhat easier to implement if you first set the output to something completely different from both strings a and b and then iteratively refine it, always maintaining the invariant that it is equidistant from a and b.
It's not hard to notice that, at each step, you must either change an element i such that ai = bi or change two elements i, j such that ai ≠ bi and aj ≠ bj. For more details, take a look at this code: http://codeforces.me/contest/584/submission/13449413
Nice implementation. Clear and straightforward.
Easy to understand.
I solved D by using 3 every time. I precomputed primes up to 10^6 and then tried to find the first prime p for which (n-p-3) is prime. It is always found fast enough (31 ms runtime, actually), but I have no proof of why it works.
http://codeforces.me/contest/584/submission/13480500
This also follows from Goldbach's conjecture (if it were proven), n - 3 is even so there should be two primes p1, p2 such that n - 3 = p1 + p2, or n - p1 - 3 = p2.
Yes, but there is no proof that those two primes (or at least one of them) are <= 10^6.
Well ..
https://en.wikipedia.org/wiki/Goldbach%27s_conjecture#Verified_results
If you read Wikipedia's article on Goldbach's conjecture they claim:
"3325581707333960528 is the smallest number that has no Goldbach partition with a prime below 9781".
Although I haven't gone to the source of this verification so I don't know whether it's actually true.
Notice this implies your 'search for the first prime..' part will try -possibly much- less than 10000 possible partitions.
That's funny, I literally read the whole "Verified results" section except for this last sentence. Also that's a really interesting fact, I definitely wouldn't have guessed that primes are this common. Bad intuition on my part, I guess.
This theorem might be of interest: https://en.wikipedia.org/wiki/Prime_number_theorem. Roughly, in the neighborhood of n, you can expect about one in every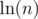 numbers to be prime. Knowing this is occasionally useful when analyzing (or designing) "brute force" algorithms that would otherwise seem to give TLE.
numbers to be prime. Knowing this is occasionally useful when analyzing (or designing) "brute force" algorithms that would otherwise seem to give TLE.
On a related note, it seems that Google once posted several recruitment billboards with the text "{first 10-digit prime found in consecutive digits of e}.com". Turns out the expected solution was just to brute force the possible sequences :)
Source: http://mathworld.wolfram.com/news/2004-10-13/google/
Can someone explain me how did he get The number of ways to choose ai = (3)^(3*n) in Problem B.
each element of a can have one of three values (1 or 2 or 3), and the number of elements of a is 3*n so the number of ways to choose the values of a = 3^(3*n)
“You can check that there is a solution for all even numbers less than 300 by bruteforce.” Actually,there is a solution for all even numbers less than 10^18. https://en.wikipedia.org/wiki/Goldbach%27s_conjecture
Can somebody explain how E solution works? I didn't understand very well the tutorial, sorry :/
Thanks.
Sure :)
Let a and b be two permutations of length n and suppose that we want to transform a into b. Now, let sx denote the position to which we want to move the value x in a -- in other words, sbi = i. The first thing to notice is that the theoretically best value for the answer is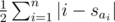 . The only way to reach it would be to move each element ai to the position sai without ever getting farther from it. And indeed, it turns out that we can always do that!
. The only way to reach it would be to move each element ai to the position sai without ever getting farther from it. And indeed, it turns out that we can always do that!
If we sequentially process elements from the right, a possible strategy is the following: visit one element at a time and, if it should be to the right, try to move it to its final position by performing swaps along the "good pairs" on the path between it and its destination. I'm calling a pair (ai, aj) "good" if swapping ai and aj moves them both closer to their final positions. (Remember, swapping a pair that isn't good would make it impossible to reach the optimal value.)
Here's my implementation: http://codeforces.me/contest/584/submission/13502664 (s in the explanation corresponds to desired_pos in the code)
johnjq , thanks for the excellent explanation, now I understood!
mras, you're welcome :)
How to prove that the solution for the problem E requires the smallest amount of money?
Because solution moves numbers only to their positions in final array
Every problem of this contest is beautiful and mathematical.
For problem D , how you have figured out maximal distance is 282?
you don't need to calculate that just we need to know that this fact exists!!
B is solvable using Binary Exponentiation in O(log(n)) https://codeforces.me/contest/584/submission/55737018
why do we need (pot_27-pot_7+MOD)%MOD? why just (pot_27-pot_7)%MOD won't work?
Edit : Figured, it's different for minus.
For problem C, Why "cdd" is not a valid solution for first test case? https://codeforces.me/contest/584/submission/68720559