| Codeforces Round 146 (Div. 1) |
|---|
| Закончено |
Вы играете в игру под названием Osu. Упрощенная версия этой игры заключается вот в чем: в игре надо кликнуть n раз. На каждый Ваш клик система выдает свой вердикт, всего существует два вердикта: верно или неверно. Обозначим вердикт верно символом «O», неверно символом — «X», тогда всю игру можно закодировать последовательностью из n символов «O» и «X».
Счет в игре вычисляется по последовательности, кодирующей игру, следующим образом: для каждого наибольшего блока из идущих подряд «O», длина блока (количество символов «O») возводится в квадрат и прибавляется к счету. Например, если Вашу игру можно представить как «OOXOOOXXOO», то есть три наибольших блока из идущих подряд «O»: «OO», «OOO», «OO», следовательно, Ваш счет составит 22 + 32 + 22 = 17. Если в процессе игры не было ни одного верного клика, счет равняется 0.
Вы знаете, что вероятность верно кликнуть в i-ый (1 ≤ i ≤ n) раз равняется pi. Иными словами, i-ый символ в последовательности, которая кодирует эту игру, может быть «O» с вероятностью pi, или быть «X» с вероятностью 1 - pi. Ваша задача — посчитать ожидаемый счет для Вашей игры.
В первой строке записано целое число n (1 ≤ n ≤ 105) — количество кликов. Во второй строке записаны n вещественных чисел через пробел p1, p2, ..., pn (0 ≤ pi ≤ 1).
Гарантируется, что заданные pi содержат не больше шести знаков после десятичной точки.
Выведите единственное вещественное число — ожидаемый счет Вашей игры. Ваш ответ будет считаться корректным, если его абсолютная или относительная погрешность не превышает 10 - 6.
3
0.5 0.5 0.5
2.750000000000000
4
0.7 0.2 0.1 0.9
2.489200000000000
5
1 1 1 1 1
25.000000000000000
Пояснение к первому примеру. Есть 8 возможных исходов. Вероятность каждого из них составляет 0.125.
- «OOO» → 32 = 9;
- «OOX» → 22 = 4;
- «OXO» → 12 + 12 = 2;
- «OXX» → 12 = 1;
- «XOO» → 22 = 4;
- «XOX» → 12 = 1;
- «XXO» → 12 = 1;
- «XXX» → 0.
Таким образом, ожидаемый счет составляет 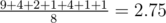 .
.
| Название |
|---|




