YuukaKazami's blog

Codeforces Round #146 Tutorial
By YuukaKazami, 12 years ago, In English

236A - Boy or Girl

It is a very simple problem, just count how many distinct chars in the input and output the correct answer.

236B - Easy Number Challenge

First of all, we can make a table of size a*b*c to store every number's d value. Then we can just brute force through every tripe to calculate the answer.

235A - LCM Challenge

It is a simple problem, but many competitors used some wrong guesses and failed. First of all, we should check if n is at most 3 and then we can simply output 1,2,6.

Now there are two cases: When n is odd, the answer is obviously n(n-1)(n-2). When n is even, we can still get at least (n-1)(n-2)(n-3), so these three numbers in the optimal answer would not be very small compared to n. So we can just iterate every 3 number triple in [n-50,n] and update the answer.

235B - Let's Play Osu!

Let us take a deep look at how this score is calculated. For an n long 'O' block, it contributes n2 to the answer.

Let us reformat this problem a bit and consider the following alternative definition of the score: (1) For each two 'O' pair which there is no 'X' between them, they add 2 to the score. (2) For each 'O', it adds 1 to the score.

We claim that this new definition of the score is equivalent to the definition in the problem statement.

Proof of the claim: For an n long 'O' block, there are Cn2 pairs of 'O' in it and n 'O' in it. Note that 2Cn2 + n = n2.

So now we work with the new definition of the score. For each event(i,j) (which means s[i] and s[j] are 'O', and there is no 'X' between them). If event(i,j) happens, it adds 2 to the score.

So we only need to sum up the probabilities of all events and multiply them by 2, and our task becomes how to calculate the sum of probabilities of all the event(i,j). Let P(i,j) be the probability of event(i,j).

We can see that P(i,j) can be computed by 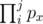. Then we denote P(j) as the sum of all event(i,j) for i<j. We have dp(0)=0 and dp(j)=(dp(j-1)+pj - 1)*pj

235C - Cyclical Quest

This problem can be solved by many suffix structures. Probably using suffix automaton is the best way to solve it since suffix automaton is simple and clear.

Let us build a suffix automaton of the input string S, and consider the query string x.

Let us also build a string t as x concatenated with x dropping the last char. One can see that every consecutive sub-string of t with length |x| is a rotation of x.

Let us read the string t with suffix automaton we have build, and every time take the first char out and add a new char, add the answer by the number of string equal to this current sub-string of t (which is a rotation of x).

And one more thing, we should consider the repetend of x as well, check my solution here:2403375.

Check here if you are not familiar with suffix automaton :e-maxx's blog

235D - Graph Game

First of all, let us consider the simpler case of trees.

Let us use Event(A,B) to denote the following event "when we select A as the deleting point, B is connected to A".

Clearly, if Event(A,B) happens, it would add 1 to totolCost.

So we can just simply calculate the probability of every Event(A,B), and add them up.

Let us consider how to calculate the probability of Event(A,B).

Assume there are n vertices in the path between A and B, we claim that the probability is simply 1 / n.

Let us try to prove it using induction.

First let us assume there's a connected sub-graph of the tree containing both A and B, if the sub-graph only has n vertices, then the event happens only if we select vertex A, so the probability is 1 / n.

Otherwise, assume it has x vertices there is two cases: whether the selected vertex is on the path between A and B or not.

In the first case, the probability of Event(A,B) happen is 1 / x because if we don't select A, Event(A,B) will never happen.

In the second case, the sub-graph containing A,B has become smaller, so the probability is (x - n) / xn.

So add them up we can prove this statement.

Then we can solve the tree case by simply add up the inverse of every path's length in the tree.

And for the original case, there's at most 2 paths between A and B.

If there's only one path, then everything is the same with the tree case.

Otherwise, the path between A and B should pass the cycle in the graph.

Let us examine this case, you can see that there 2 types of vertex:

Vertex on the path of A to cycle or B to cycle, they should not be selected before A because once they're selected, A and B lost connectivity, let us call them X.

Vertex on the cycle, the two paths from A to B, each path contains a path in the cycle, let us call them Y and Z.

So there are two possibilities: X and Y are free when A is selected, X and Z are free when A is selected.

And we should subtract the case that X and Y, Z are all free when A is selected because it double-counts before.

So the probability is 1 / (X + Y + 1) + 1 / (X + Z + 1) - 1 / (X + Y + Z + 1).

Check Petr 's solution for the details: 2401228

And my C++ implementation: 2403938

235E - Number Challenge

Let us consider each prime in one step, the upper limit for a, b, c is recorded.

So if we fixed the power of 2 in each i, j, k like 2x, 2y, 2z, then their upper limit becomes a / 2x, b / 2y, c / 2z, and the power of 2 in their multiplication is just x+y+z.

Let us denote dp(a, b, c, p) for the answer to the original problem that i, j, k 's upper limit is a, b, c. And their can only use the prime factors which are not less than p.

Let the next prime to be q, so we can try to fix the power of p in i, j, k and get the new upper limit.

So we can do transform like this: dp(a, b, c, p) = sum of dp(a / px, b / py, c / pz, q)·(x + y + z + 1)

Check my code here: 2404223

Also you can check rng_58 solution here: http://codeforces.me/blog/entry/5600

If you have any problems, you can ask here :)

  • Vote: I like it
  • +69
  • Vote: I do not like it

Comments Comments (76)
| Write comment?
»
12 years ago, # |
  Vote: I like it +2 Vote: I do not like it

actually i m not able to get anything from your java code in cyclical quest Div-2 E . someone please explain it with the help of his c++ code

Thank You,

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Oh...I think you should learn suffix automaton first if you want to understand it..I'll post some good materials about suffix automaton in the tutorials...after you learned suffix automaton, it's easy to solve this problem.

    → Reply
»
12 years ago, # |
← Rev. 4   Vote: I like it +6 Vote: I do not like it

I have better sol for Div 1.A only like this 

readln( n );
                if n = 1 then Result( 1 );
                if n = 2 then Result( 2 );
                if n = 3 then Result( 6 );
                if odd( n ) then
                        res := n * ( n - 1 ) * ( n - 2 )
                else
                        begin
                                if n mod 3 = 0 then
                                        res := ( n - 1 ) * ( n - 2 ) * ( n - 3 )
                                else
                                        res := n * ( n - 1 ) * ( n - 3 );
                        end; 
                Result( res );

Div 1.B, I think Ray030123 has better solution :)

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    yeah this is the perfect sol. for it..

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Oh, thank you for translating my Python code here. * P.S. It's ray0(4)0123

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Please, can you tell why it's true?

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      If n mod 2 = 1 => res = n * ( n — 1 ) * ( n — 2 )

      Of course it is, right ???

      if n mod 2 = 0 { We can see that n and ( n — 2 ) have GCD is 2 => res = n * ( n — 1 ) * ( n — 2 )/2 It's is small, so we think about n * ( n — 1 ) * ( n — 3 ) But if n mod 3 = 0 we can see that the result is smaller :( So we think about ( n — 1 ) * ( n — 2 ) * ( n — 3 ) You should think more careful and then you will know why :D }

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I dont think that ur saying if n mod 3 = 0 we can see result will be smaller is right, i think then n and n — 3 will no longer be co-prime in that case

        → Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    You can make it more easier n = int(input()) if n==1 or n==2: print(n) exit() if n&1: print((n)*(n-1)*(n-2)) else: print(max(n*(n-1)*(n-3), (n-1)*(n-2)*(n-3)))

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Faaaar better than what is given in the official solution. I was not able to understand that 50 but here it's all understandable.

    → Reply
»
12 years ago, # |
  Vote: I like it +11 Vote: I do not like it

How do you solve C using a different suffix structure? Say a suffix array.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Let us build a suffix array of s and concatenate those t-string made from x to its back.

    then we can find each rotation's occur time in string s.

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Could you give more detailed explanation of this solution, please?

      How do we use suffix array to solve this problem?

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Same question.

        → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it +13 Vote: I do not like it

        Firstly we should concatenate original string S and all the query strings (each doubled without last symbol), put different symbols between strings (e.g. 300, 301,..., it would be array of ints, not chars), then make a suffix array on that concatenated string. We will have 2 arrays — sorted suffixes of all the strings and lengths of common prefixes between them. Then we should build segment tree on the array of lengths to be able to quickly find minimum number on the any segment. Then iterate on the array of suffixes. For each suffix of query string we firstly should determine weather we use it (i.e. it is not equal to another shift of this query). We can determine it by getting the minimum number on the array of lengths between past occurrence of this query and current one. If we use it we should determine the number of suffixes of S that have common prefix with it not less than length of this query. We can calculate it by using binary search and segment tree (complexity O(log^2(n))) or by using treap (complexity O(log(n)))

        → Reply
        • »
          »
          »
          »
          »
          12 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Sounds nice. Did you try it though? I just coded it up, and can't get it to work in time. I construct the 3-million suffix array in 3 seconds and the rest of my code is O(n log n).

          → Reply
          • »
            »
            »
            »
            »
            »
            12 years ago, # ^ |
              Vote: I like it +18 Vote: I do not like it

            I have read your solution,It seem 3-million suffix array is too slow. well, There is a way using only 1-million suffix array construction.

            You just construct the suffix-array of the string S. Then for each query x,binary-search the position in SA in O(logn+|x|),then you need add a char at the front to x and delete a char at end of it.

            if we know the position of x in SA, then cx's position(means add a char at the front of x) can be calculated in O(log n) as well, when comparing cx to a suffix,you first compare the first char, then compare x to the suffix' next suffix(which we already know).

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              12 years ago, # ^ |
                Vote: I like it +5 Vote: I do not like it

              Yeah, this back-stepping method (x -> cx) is what I've been missing during the contest. I'll try to code it up later. Thank you!

              → Reply
»
12 years ago, # |
  Vote: I like it +6 Vote: I do not like it

My Div1A problem got accepted but I have no idea about the proof of the solution... can anyone provide me some??.........

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 235B, what do you mean by: 

So if they are i, j , ....
→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I means if the two 'O' in the pair have indexes i and J.

    → Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in div 2 problem C i am not able to understand why 50,,,,, why to check for triplet having greatest lcm in the range [n-50,n]

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    me, too. i've checked only triplets with n..n-5 at most and it get AC. Well, thanks to the author for good problemset (esp. for me, learning Math), but i expected to see some more strict manual with good explanation, why it goes well. "good" brute force is not the answer, you know...

    → Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    50 is the upperbound, it is a aproximation solution. You can use 100 too.

    → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I used [n — 3, n] and it got AC.

    → Reply
»
12 years ago, # |
  Vote: I like it -23 Vote: I do not like it

in Problem "Lets play Osu", i am not able to understand what to do from the editorial... if u are writing the editorial make sure that u explain well and not 2 line explanation,,, learn something from Topcoder.com on how to write good editorials,,, being red doesnt mean that everyone is as experienced as u ..... we need good guidance.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    So we had some sort of common problem (all wars come from it, i assure you) — "mis-", "not-" and "not full-" "-understanding". Please dont get me wrong.

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Oh...I'll try to make it more clear today...But your handle say you're a red coder though :)

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it -15 Vote: I do not like it

      in India programming is not as good as in Russia or china or japan... but i assure u if i get good guidance i would definitely do better... can u give me ur Email id or Facebook Link so that i can contact u when having some trouble.. :)

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
        ← Rev. 2   Vote: I like it +56 Vote: I do not like it

        http://ask.fm/WJMZBMR

        anyway...I don't think born in India is an excuse, Actually I learned programming all from internet resource in English.As you are an India, I bet your English is better than mine.Just work harder bro.

        → Reply
»
12 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you provide an English paper about suffix automata ?? Thank you . Chinese paper is also OK for me :)

→ Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Shouldn't the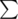 in solution for 235B be a ?

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What happens after 235D — Graph Game is extended to a normal graph?

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think then it is totally unsolvable.

    To the least you can use a O(2^n) dp instead.

    But It can be solved in cactus, and the first version of this problem is on cactus, I think that is too hard so I simplify a bit.

    → Reply
»
12 years ago, # |
  Vote: I like it -7 Vote: I do not like it

orz))))

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem "Let's Play Osu!":

"It can be interpreted as, 2*number of pair of 'O' in this 'O' block + number of 'O' in this 'O' block."

What was the motivation for this? Or is it just experience? :)

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Well, some thoughts just came out...It is hard to give a exact motivation...

    → Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    If you are looking for proof for the statement, then n^2 = (1+1+1....n times)^2 = 1^2 + 1^2 +..n times + 2 * (all combinations of 1s...nC2 times) However, I can still not see an O(n) approach using the explanation. I wish if someone can show me an implemented solution using the above insight.

    I solved the problem using the observation, that if an O is added at the end and we know the expected value(let say, X) of Os at the end then the score would increase by (X+1)^2 -X^2 = 2*X + 1

    → Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://www.codeforces.com/contest/235/submission/2408731

http://www.codeforces.com/contest/235/submission/2408690

These are the link of my submission for Div1 problem E. The first one is Accepted and the second one is getting TLE. But the only difference of the solutions is that I called from last prime to the first prime in the first and in the second one was the reverse(From the first prime to the last).... the rest solutions are the same... but I have no Idea why it is happening so.... Am I missing something obvious?

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If you have time, please comment part of your code. I solved some simple tasks using Suffix Automaton (those described in e-max blog) but it seems that you are augmenting the data structure. I can't understand the meaning of "nxt" nor "repetend".

sorry for troubles and thank you.

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's just a kmp-algorithm to get the repetend of the query x_i

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      thank you for your answer. i broke my mind for hours until i came up with a solution. after that, i went back to your code and could understand almost everything.

      → Reply
»
12 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

I tried that link on suffix automatons. I translated it with Google Translate. I could not understand what this means:

-------- Consider any non-empty substring t line s . Then called the set of endings endpos (t) set of all positions in the line s In which the end of the lines with t .

We will call two substrings t_1 and t_2endpos Equivalent if their sets of endings are the same: endpos (t_1) = endpos (t_2) . Thus, all non-empty substrings s can be divided into several classes according to their equivalence sets endpos . --------

I get it that "line s" means "string s". I am confused as to what is meant exactly by endpos(t). Does it mean all suffixes which end with 't'? And what is the significance of two substrings being endpos equivalent?

Thanks.

→ Reply
»
12 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Please could anyone shed more light on the Let's Play Osu problem...I still haven't gotten the main idea...

Thank You!!!

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Same problem with me.... Please someone explain deeply how to solve Let's Play Osu....

    → Reply
    • »
      »
      »
      12 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I am very busy this week(I'm a high-school student and have to go to school)...well,I'll do it tonight...

      → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        thats ok :)

        → Reply
      • »
        »
        »
        »
        12 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        pls explain one thing , in Lets Play Osu problem we have to consider each pair of O's so why u said consider only those pair of O's having no X between them....,

        → Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I tried a lot but did not understand the editorial of 235E Number Challenge. Somebody please explain in detail.

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Excellent idea on problem D in Div2. Is there any background? I don't think I can come up with this idea if I didn't see ti before.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

WJMZBMR, your English is not very good. I'm hardly understanding what you meant in the post.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Dude, despite his english he has written a decent editorial and clarified everyone's doubts in the comments. You cannot expect everyone to know good English. It's just another language!

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You are right, dude. I want too much.

      → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

if in the problem A wanted to find the ressult with 4 distinct number what would be the result????????

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I can't understand the div1B idea Could someone explain it me please?

→ Reply
»
6 years ago, # |
  Vote: I like it +12 Vote: I do not like it

The editorial includes almost no explanation at all for the div2 E / div1 C problem except for telling that suffix automaton may be used and we should construct a string $$$t$$$ that is $$$(x + x)$$$ but doesn't include the last char.

Here is my approach for the problem using suffix automaton:

Note: The terminology used will be in reference to this article for suffix automaton.

We start by building suffix automaton on $$$s$$$. Let $$$t$$$ be the string as mentioned above for the query string $$$x$$$. As noted, a substring of length $$$|x|$$$ of $$$t$$$ is a rotation of $$$x$$$.

Firstly, we precompute a $$$dp$$$ table using the SA: $$$dp[i]$$$ = No. of terminal nodes reachable from the $$$i$$$-th node. This will tell us how many suffixes can be attached to the current substring when we are at node $$$i$$$, which will give us the no. of times the current substring occurs as a substring in $$$s$$$. This is because a substring is just a prefix of some suffix and $$$dp[i]$$$ tells us exactly how many suffixes can be attached to the current substring to make a suffix, such that the current substring will be a prefix for them.

Now, let's have $$$2$$$ pointers (indices) $$$i$$$ and $$$j$$$ in $$$t$$$, $$$j$$$ points to the next char in $$$t$$$ that needs to be concatenated to the current string and $$$i$$$ tells us that we are considering the substring of $$$t$$$ starting at position $$$i$$$. To get all cyclic shifts, we iterate $$$i$$$ from $$$0$$$ to $$$(m-1)$$$. When we are at $$$i$$$, we'll have to extend our substring to include char $$$t[j]$$$ and drop the char $$$t[i-1]$$$. To drop the $$$(i-1)st$$$ char, note the $$$minlen$$$ of the current node, using the fact that $$$minlen(cur) = len(link(cur)) + 1$$$. If $$$minlen(cur) \le len$$$, the substring $$$t[i..j-1]$$$ will be found at the cur node, and we do not need to move to any other node. If however, $$$minlen(cur) > len$$$ (more precisely, $$$minlen(cur) == len + 1$$$), the substring $$$t[i..j-1]$$$ cannot be found at the current node, so we follow the suffix link to go to the node where it will be found and set that to the new cur node. After dropping $$$t[i-1]$$$, the string we have corresponds to $$$t[i..j-1]$$$. So, its length, $$$len = (j - i)$$$.

Now, we will try to extend our current string to be of length $$$m = |x|$$$ (if possible). That is, while $$$(j - i) < m$$$ and there is a transition possible from state $$$cur$$$ corresponding to $$$t[j]$$$, we'll make the transition and set $$$cur$$$ to the node at the other end of the transition. After that, we'll check to see if we have found a string of length $$$m$$$ or not. If $$$(j - i) < m$$$, we did not find the string of length $$$m$$$ starting at $$$t[i]$$$ to be present in the SA (or in the string $$$s$$$), so we continue our procedure by incrementing $$$i$$$ to consider the next substring. If however $$$(j - i) == m$$$, we have found the string starting at $$$t[i]$$$ in $$$s$$$, so we add $$$dp[cur]$$$ to the answer.

There is one technical detail missing in the above explanation. Consider the case when a substring is occurring more than once as a cyclic shift. For example, if $$$x =$$$ "$$$aa$$$", then $$$t[0..1] = t[1..2] =$$$ "$$$aa$$$". So, the substring "$$$aa$$$" would get counted twice, however we need every substring exactly once in the answer. To avoid this, note that for two $$$m$$$ length strings to be identical, we must be at the same state in the SA when considering these two strings. This follows from the properties of SA, since a state can correspond to atmost one string of length $$$m$$$. So, we may keep a set of visited states and if $$$cur$$$ state has already been visited, we do not add $$$dp[cur]$$$ to the answer to avoid overcounting.

Here is my solution using this idea: 51809558

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

I developed the following intuition for Div1 A. Our final aim is to reduce the number of common factors between as large numbers as allowed so as to get the largest LCM. So, firstly, if the numbers are <= 3, we have no choice but to output 1, 2 (1 * 2), 6(1 * 2 * 3) respectively. Now n can be either even or odd. We know that no two consecutive odd numbers have a common factor other than 1. So, in case n is odd, we can go ahead and output n * (n — 1) * (n — 2). Clearly, n and n — 2 don't share any common factor here, nor does n — 1 have a common factor with either of these ( also not that n — 1 will be even while others are odd).

Now when n is even. If we go like odd numbers and output n * (n — 1) * (n — 2), we might be wrong due to the following reasons.

  1. n and n — 2 actually share a common factor, which is 2.

  2. So should we go and output n * (n — 1) * (n — 3) then ? NO. What if n was divisible by 3 too ? Now, we are actually including n and n — 3, that both share 3 as a common factor, and thus will end up with a wrong answer ! So, there are two sub cases: 2.1) n is divisible by 3. If that is the case we output (n — 1) * (n — 2) * (n — 3). Clearly n — 1 and n — 3 are odd and don't share any common factor, nor does n — 2, which is even. 2.2) n not divisible by 3. In this case we can easily go ahead with n * (n — 1) * (n — 3) !

I hope this helps.

My code: https://codeforces.me/problemset/submission/235/52744967

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 235A LCM Challenge, (n-1)*(n-2)*(n-3) doesn't works when input is 10...

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    That's because n*(n-1)*(n-3) gives a better solution when n is even but not divisible by 3.

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 235A, I managed to solve the problem as follows in O(1):

  1. If n = 1, ans = 1.

  2. If n = 2, ans = 2.

  3. If n is odd, ans = n * (n — 1) * (n — 2).

  4. If n is even and divisible by 3, ans = (n — 1) * (n — 2) * (n — 3).

  5. If n is even but not divisible by 3, ans = n * (n — 1) * (n — 3).

Here is my submission: 73660151

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    valdaarhun How this works when n is even?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      If n is even, then you definitely can't do n*(n-1)*(n-2) because n and n-2 won't be coprime.

      So you can either do n*(n-1)*(n-3) or (n-1)*(n-2)*(n-3).

      Now, in both the above expressions, the n-1 and n-3 terms are common. So it would make sense to use the first expression, i.e. n*(n-1)*(n-3). But there is a catch. If n is a multiple of 3 then you can write n as 3a. But then n and n-3 will not be coprime anymore. In that case you would have to use the second expression, i.e. (n-1)*(n-2)*(n-3)

      → Reply
»
4 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Idea of 235B was slick! YuukaKazami

→ Reply