| Codeforces Round 943 (Div. 3) |
|---|
| Закончено |
Дано целое число $$$n$$$. Вы выбираете $$$n$$$ ячеек $$$(x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)$$$ в сетке $$$n\times n$$$, где $$$1\le x_i\le n$$$ и $$$1\le y_i\le n$$$.
Пусть $$$\mathcal{H}$$$ — множество различных манхеттенских расстояний между любой парой ячеек. Ваша задача — максимизировать размер $$$\mathcal{H}$$$. Примеры множеств и их построение приведены в пояснении.
Если существует более одного решения, вы можете вывести любое из них.
Манхеттенское расстояние между ячейками $$$(x_1,y_1)$$$ и $$$(x_2,y_2)$$$ равно $$$|x_1-x_2|+|y_1-y_2|$$$.
Первая строка содержит одно целое число $$$t$$$ ($$$1\le t\le 50$$$) — количество наборов входных данных.
Каждая из следующих $$$t$$$ строк содержит одно целое число $$$n$$$ ($$$2\le n\le 10^3$$$).
Для каждого набора входных данных выведите $$$n$$$ точек, которые максимизируют размер $$$\mathcal{H}$$$. Выводить пустую строку в конце ответа для каждого набора входных данных не обязательно.
523456
1 1 1 2 2 1 2 3 3 1 1 1 1 3 4 3 4 4 1 1 1 3 1 4 2 1 5 5 1 4 1 5 1 6 5 2 5 5 6 1
В первом примере $$$n=2$$$. Одно из возможных расположений:
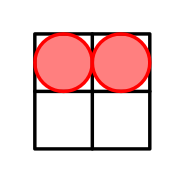 Расположение с ячейками в $$$(1,1)$$$ и $$$(1,2)$$$.
Расположение с ячейками в $$$(1,1)$$$ и $$$(1,2)$$$. Во втором примере $$$n=3$$$. Оптимальное расположение:
 Расположение с ячейками в $$$(2,1)$$$, $$$(2,3)$$$ и $$$(3,1)$$$.
Расположение с ячейками в $$$(2,1)$$$, $$$(2,3)$$$ и $$$(3,1)$$$. $$$\mathcal{H}$$$=$$$\{|2-2|+|1-1|,|2-2|+|3-3|,|3-3|+|1-1|,|2-2|+|1-3|,|2-3|+|1-1|,|2-3|+|3-1|\}$$$=$$$\{0,0,0,2,1,3\}$$$=$$$\{0,1,2,3\}$$$.
Для $$$n=4$$$ возможное расположение:
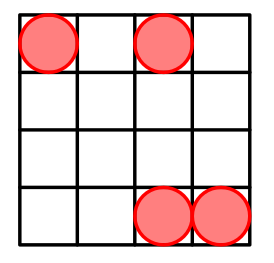
Для $$$n=5$$$ возможное расположение:

Для $$$n=6$$$ возможное расположение:
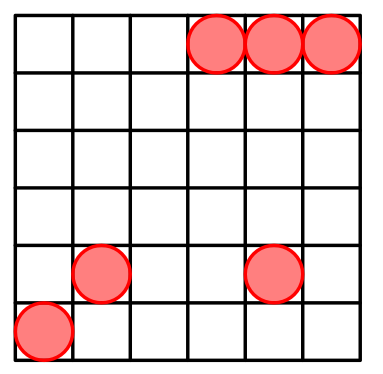
| Название |
|---|




