We thank everyone who participated in the round.
Author: JuicyGrape
Try to find the upper bound of $$$\gcd(x,y)+y$$$.
$$$\gcd(x,y)+y=\gcd(x-y,y)+y$$$.
$$$\gcd(x,y)+y\le x$$$. Try to find such $$$y$$$, that $$$\gcd(x,y)+y=x$$$?
#include<iostream>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int x;
cin>>x;
cout<<x-1<<"\n";
}
}
Author: FBI
Try to check for every $$$k$$$ if the prefix of $$$a$$$ of length $$$k$$$ is a subsequence of $$$b$$$.
#include<iostream>
#include<vector>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int n,m;
cin>>n>>m;
vector<char>a(n+1),b(m+1);
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=m;i++){
cin>>b[i];
}
vector<int>dp(m+1);
dp[1]=(a[1]==b[1]?1:0);
for(int i=2;i<=m;i++){
if(dp[i-1]!=n && b[i]==a[dp[i-1]+1]){
dp[i]=dp[i-1]+1;
}else{
dp[i]=dp[i-1];
}
}
cout<<dp[m]<<"\n";
}
}
1968C - Assembly via Remainders
Author: JuicyGrape
Why constraints are small?
Try to think about increacing $$$a_1,\dots,a_n$$$.
$$$((a + b)\bmod a) = b$$$ for $$$0\le b < a$$$.
#include<iostream>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int S=1000;
cout<<S<<" ";
for(int i=2;i<=n;i++){
int x;
cin>>x;
S+=x;
cout<<S<<" ";
}
cout<<"\n";
}
}
Author: FBI
Consider a cycle of the permutation.
When it is optimal to stay on the same place till the end of the game?
#include<bits/stdc++.h>
using namespace std;
long long score(vector<int>&p,vector<int>&a,int s,int k){
int n=p.size();
long long mx=0,cur=0;
vector<bool>vis(n);
while(!vis[s]&&k>0){
vis[s]=1;
mx=max(mx,cur+1ll*k*a[s]);
cur+=a[s];
k--;
s=p[s];
}
return mx;
}
int main(){
int t;
cin>>t;
while(t--){
int n,k,s1,s2;
cin>>n>>k>>s1>>s2;
vector<int>p(n),a(n);
for(auto&e:p){
cin>>e;
e--;
}
for(auto&e:a){
cin>>e;
}
long long A=score(p,a,s1-1,k),B=score(p,a,s2-1,k);
cout<<(A>B?"Bodya\n":A<B?"Sasha\n":"Draw\n");
}
}
Author: JuicyGrape
What is the maximal possible size of $$$\mathcal{H}$$$?
Can you always get that size for $$$n\geq 4$$$?
Consider odd and even distances independently.
Let us find an interesting pattern for $$$n\geq 4$$$.
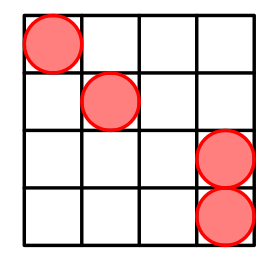
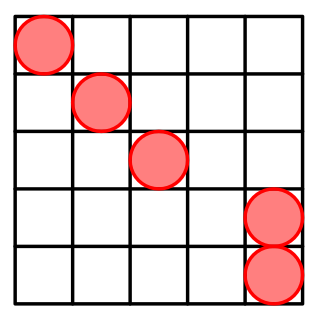
Can you generalize the pattern? We put $$$n-2$$$ cells on the main diagonal. Then put two cells at $$$(n-1,n)$$$ and $$$(n,n)$$$.
But why does it work? Interesting fact, that in such way we generate all possible Manhattan distances. Odd distances are generated between cells from the main diagonal and $$$(n-1,n)$$$. Even distances are generated between cells from the main diagonal and $$$(n,n)$$$.
#include<iostream>
using namespace std;
int main(){
int t;
cin>>t;
while(t--){
int n;
cin>>n;
for(int i=1;i<=n-2;i++){
cout<<i<<' '<<i<<"\n";
}
cout<<n-1<<' '<<n<<"\n"<<n<<' '<<n<<"\n";
}
}
Author: JuicyGrape
Is it useful to divide the segment into more than three segments?
Use the fact, that $$$x\oplus x=0$$$ and $$$x\oplus x\oplus x=x$$$.
When you can divide the segment into $$$2$$$ parts?
When can you divide the segment into $$$3$$$ parts?
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
int a[N];
int main(){
int t;
cin>>t;
while(t--){
int n,q;
cin>>n>>q;
map<int,vector<int>>id;
id[0].push_back(0);
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]^=a[i-1];
id[a[i]].push_back(i);
}
while(q--){
int l,r;
cin>>l>>r;
if(a[r]==a[l-1]){
cout<<"YES\n";
continue;
}
int pL=*--lower_bound(id[a[l-1]].begin(),id[a[l-1]].end(),r);
int pR=*lower_bound(id[a[r]].begin(),id[a[r]].end(),l);
cout<<(pL>pR?"YES\n":"NO\n");
}
if(t)cout << "\n";
}
}
1968G1 - Division + LCP (easy version)
Author: JuicyGrape
Binary search.
How to check if two strings are equal?
#include<bits/stdc++.h>
using namespace std;
vector<int>Zfunc(string& str){
int n=str.size();
vector<int>z(n);
int l=0,r=0;
for(int i=1;i<n;i++){
if(i<=r){
z[i]=min(r-i+1,z[i-l]);
}
while(i+z[i]<n&&str[z[i]]==str[i+z[i]]){
z[i]++;
}
if(i+z[i]-1>r){
l=i;
r=i+z[i]-1;
}
}
return z;
}
int f(vector<int>&z,int len){
int n=z.size();
int cnt=1;
for(int i=len;i<n;){
if(z[i]>=len){
cnt++;
i+=len;
}else{
i++;
}
}
return cnt;
}
int main(){
int t;
cin>>t;
while(t--){
int n,k;
string s;
cin>>n>>k>>k>>s;
vector<int>z=Zfunc(s);
int l=0,r=n+1;
while(r-l>1){
int mid=(l+r)/2;
if(f(z,mid)>=k){
l=mid;
}else{
r=mid;
}
}
cout<<l<<"\n";
}
}
1968G2 - Division + LCP (hard version)
Author: JuicyGrape
Consider the general case: $$$L=1$$$ and $$$R=n$$$.
You must find the answer for each $$$k$$$ in the range $$$[1,n]$$$. Consider the cases $$$k\le \sqrt{n}$$$ and $$$k\geq \sqrt{n}$$$.
#include<bits/stdc++.h>
using namespace std;
vector<int>Zfunc(string& str){
int n=str.size();
vector<int>z(n);
int l=0,r=0;
for(int i=1;i<n;i++){
if(i<=r){
z[i]=min(r-i+1,z[i-l]);
}
while(i+z[i]<n&&str[z[i]]==str[i+z[i]]){
z[i]++;
}
if(i+z[i]-1>r){
l=i;
r=i+z[i]-1;
}
}
return z;
}
int f(vector<int>&z,int len){
int n=z.size();
int cnt=1;
for(int i=len;i<n;){
if(z[i]>=len){
cnt++;
i+=len;
}else{
i++;
}
}
return cnt;
}
int main(){
int t;
cin>>t;
while(t--){
int n,L,R;
string s;
cin>>n>>L>>R>>s;
vector<int>z=Zfunc(s);
const int E=ceil(sqrt(n));
vector<int>ans(n+1);
for(int k=1;k<=E;k++){
int l=0,r=n+1;
while(r-l>1){
int mid=(l+r)/2;
if(f(z,mid)>=k){
l=mid;
}else{
r=mid;
}
}
ans[k]=l;
}
for(int len=1;len<=E;len++){
int k=1;
for(int i=len;i<n;){
if(z[i]>=len){
k++;
i+=len;
}else{
i++;
}
}
ans[k]=max(ans[k],len);
}
for(int i=n-1;i>=1;i--){
ans[i]=max(ans[i],ans[i+1]);
}
for(int i=L;i<=R;i++){
cout<<ans[i]<<' ';
}
cout<<"\n";
}
}










any good resources or blogs to explain Z-function?
Here or here
This is KMP but literally the same thing that was required for G1/G2.
https://cp-algorithms.com/string/prefix-function.html#:~:text=%C2%B6-,Search%20for%20a%20substring%20in%20a%20string.%20The%20Knuth%2DMorris%2DPratt%20algorithm,-%C2%B6
usaco.guide
codeforces edu
CSES CP book has a dedicated chapter (Advanced topics -> String algorithms -> Z-algorithm) for this topic, and personally I find its explanation really friendly.
I was thinking too complex at the problem D
same.
so do I
LOL same
Me too!
I also lies in the same category. :")
Good way to express!
the same bro
Can someone make clear how did the first question really work, I mean I thought about doing it in the same way as you've explained but I saw that some of the test cases doesn't work by that implementation on the test cases 1000 => 750 and on some other test cases, how please???
It says to print out any possible(maintaining the statement) value of y. so printing out 750 or 500 or even 999 will be allowed in this case.
Oh yeah it worked thanks bro
Should Problem B be just a 2 pointer problem with a time complexity of O(min(a, b))?
Yeah,that is one of the possible solutions. However, it is easier to explain the dp solution)
There exists an $$$\mathcal{O}(n \log^2 n) $$$ solution with a very good constant factor for G2, reply to this if interested.
I just thought of one too. Does it involve sorting and parallel binary search?
You don't need any of that. You could simulate what you do in G1 with a set/segment tree by iterating over the lengths, and it works. The time complexity came from harmonic series and the log from DS.
There also exists an O(n log n) solution using DSU.
Not sure what “parallel binary search” means, but it is nested binary search. I don't sort anything.
Basically, we still have our nice $$$z$$$ function, however, we will also store an RMQ which can get the maximum value of $$$z_i$$$ for all $$$i$$$ in a range $$$[l, r]$$$.
Let's precompute the value $$$mx_i = \text{maximum number of disjoint substrings with length } i, \text{which are all equal to the prefix of length } i$$$
If we want to check if $$$k$$$ disjoint substrings are possible with $$$\text{LCP}$$$ $$$l$$$, we just check if $$$mx_{l} \ge k$$$.
Now the problem is the computation of $$$mx$$$.
For length $$$i$$$, there can be at most $$$\frac{n}{i}$$$ disjoint substrings with that length. Let's use the fact that $$$\sum_{i=1}^{n}\frac{n}{i}=\mathcal{O}(n \log n)$$$.
Using our RMQ, we can, instead of calculating $$$mx_i$$$ in linear time in the length, we can calculate it in $$$\mathcal{O}(mx_i \log n)$$$, simply binary search on the next $$$j$$$ such that $$$z_j \ge i$$$ (here, we binary search and use a sparse table to get this next $$$j$$$ in $$$\mathcal{O}(\log n)$$$, alternatively, you can walk on a segment tree in $$$\mathcal{O}(\log n)$$$).
The complexity of this computation is $$$\sum_{i=1}^{n}mx_i\cdot \log n = \log n \sum_{i=1}^{n} mx_i \le \log n \sum_{i=1}^{n}\frac{n}{i}=\mathcal{O}(n \log^2 n)$$$
In G2 for every l <= i <= r, I used binary search and memorized answer for mid. Solution
Yes, that is my AC submission after the contest. I was able to show a loose upper bound (not in terms of $$$n$$$, but more like the maximum possible number of operations).
My code is almost exactly similar to yours, but it is getting tle on tc 13, could you take a look at it please?
296358703
RMQ is quite overcomplicated, I just used a set 259230125
Can somebody tell how to do G1 using KMP? I don't know KMP well enough to manipulate it.
FOR G2: answer f(x) is decreasing function, so i just modified simple binary search solution for G1, by just changing the upperlimit as previous answer.
Code: 259245908
I am not able to prove this tho... please help me.
Same this is what I did but dont know why it works. Did you get the proof?
Thanks for your brilliant problems! Round was fun enough to spend full competition time just solving the problem.
Can anyone explain why Sasha is the winner in the second test of problem D?
k -> 8; pb — 2; ps — 10 path -> 3 1 4 5 2 7 8 10 6 9 score-> 5 10 5 1 3 7 10 15 4 3
If both play optimally: Bodya sticks to his current position. Score -> k*score[i] -> 10*8 -> 80 Sasha moves the highest score possible and sticks there. Score -> 3+4+7+10*(15*4) -> 84
Thus, Sasha is the winner. I hope you understand:)
Yes, thanks for the explanation.
Can someone please tell me what's the rating of problem D? I'm asking because the rating is not updated on the problem tag.
clist said it was 1349 at the time I wrote this comment. I personally would say it might be around 1200-1300.
Around 1300
For B: Optimise Answer
Made video editorials for C,D,E for whoever wants to refer
C : https://www.youtube.com/watch?v=oEx5rR4wAKw
D : https://www.youtube.com/watch?v=XBUN4LwolEM
E : https://www.youtube.com/watch?v=DObsk_Rlhg8
language => Hindi
In problem F, my submission 259182179 has been hacked. But I resubmit it and got AC... Could anyone tell me why???
Testset hasn't been updated yet, all AC solutions will be retested during some hours with updated tests
Your resubmission will soon give WA verdict after system testing. In current System's all testcases are those that were during the contest [where u got AC]. Now, all the testcases that could hack other's solution, will be added in the System testcases[including the testcase that could hack ur F no. solution] and System test will run again. Then, u will get a different verdict.
Uphacked as per your wish :) now it should be automatically added to the tests already.
:((((((((((
btw, is other solutions (259304100 and 259314753) hackable?
259304100: Probably yes 259314753: No
It's all about smashing
unordered_map, you can check the generator I used once system test is done.thx a lot :D
fine... new submission has been uphacked :(
i should use map replace unordered_map
G1/G2 can be solved without any fancy algorithms as in my rust solution in C++ too: 259314092
My G1 C++ submission was the same but it was hacked
This? You should implement it more carefuly, look at Complexity section for string +=
Maybe
CAN YOU explain how it works
Count number of non-overlapping occurrences of prefix of length lcp in s. Then binary search lcp, then cache it, then find ans for every k in $$$[l..r]$$$.
I also solved G1 without using any string algorithm during the contest, but after main tests I got TLE :(
And TLE in main test:(
We may use kmp or hash or other algorithm to search a substring in $$$O(n+m)$$$ time, and a simple brute force can become $$$O(nm)$$$ in the worst cases.
Yes, the built-in find in c++ is too slow for it.
Yes. Also, what is funny is that your solution that passes on G2, doesn't pass on G1. They probably forgot to add the same test case on G2 and no one hacked it.
I assumed G2 includes all tests from G1, but then checked it on G1 and finally got my TLE :)
Interesting that Rust uses Two-way matching and passes easily. The same algorithm is said to be used in std::strstr, I tried it: 259358346 and it doesn't even pass G2.
Just bc G1 had TL 2sec when G2 had 3sec. I'll remember this for next contests :(
That's not the root cause, for sure. G2 AC in 1.7sec: 259346859 (while doing much more work) and exactly same code TLEs in G1: 259347015
I think it's ok that simpler problems have lower time limit.
Doesn't kmp takes overlapping patterns into consideration as well? How to remove that?
Is this solution for G2 hackable? Using two heurestics:
1) Memoising the value of cnt calculated in f(mid)
2) Since the answer always decreases on increasing k, keeping the value of hi from previous k(not setting it to n again).
Not able to proove it's time complexity.
I have done the same thing, and I was able to prove the complexity to some extent. It's easy to see that my code is $$$\mathcal{O(n\cdot\text{number of distinct values of } mid})$$$.
First let's assume $$$l=1$$$ and $$$r=n$$$, the binary search ranges are $$$[1,n],[1,\frac{n}{2}],\dots,[1,\frac{n}{n}]$$$.
The main observation is this, the range $$$(\frac{n}{2},n]$$$ is exposed to $$$1$$$ binary search, the range $$$(\frac{n}{3},\frac{n}{2}]$$$ is exposed to $$$2$$$ binary searches. Similarly, the range $$$(\frac{n}{i},\frac{n}{i-1}]$$$ is exposed to $$$i-1$$$ binary searches.
It is clear that with this, we have a very loose upper bound of $$$O(n\cdot\sum_{i=2}^{n}\min((i-1)\cdot\log(n), \frac{n}{i-1}-\frac{n}{i})$$$. However, as i said, this is very loose, as the sum $$$\sum_{i=2}^{n}(i-1)\cdot\log(n)$$$ is quite a bit more than $$$n\cdot\log(n)$$$ (the total number of
checks).We can make this tighter.
Let's consider the ranges $$$1$$$ by $$$1$$$, first we have the range $$$(\frac{n}{2}, n]$$$. We have $$$2$$$ cases, the first case is that $$$\log(n)$$$ is smaller than the range, in which case (for the sake of an upper bound), we should assume that we take all the $$$\log(n)$$$
checks from that range, becuase we will never see that range again, so it is best to take as much as we can from that range, hence decreasing the number of times the other ranges can be chosen by $$$\log(n)$$$.However, if the range length is less than $$$\log(n)$$$, then all the next ranges are also smaller than $$$\log(n)$$$. So in fact, a better upper bound is $$$\mathcal{O(n\cdot\sum_{i=2}^{n}\min(\log(n),\frac{n}{i-1}-\frac{n}{i}))}$$$, this value is $$$733800000 \approx 7\times 10^8$$$ for $$$n=2\cdot 10^5$$$.
The point where the minimum changes from $$$\lg n$$$ to $$$n/(i-1)-n/i$$$ will be $$$i\approx i_0=\sqrt{n/\lg n}$$$, so this analysis gives a runtime bound proportional to around $$$n\cdot ((n/i_0)+(\lg n)\cdot i_0)=2 n \sqrt{n \lg n}$$$.
Can someone please explain D as why greedy works. like can't a player stay at position for more than 1 time and then move to next one to get best answer. Its's confusing to think that he will move only by staying once or either staying all rest of left moves on that positions.
Won't it also depend on array A's elements as to loose some chances in low points in pursuit of bigger points to get maximum answer.
i still can't get how greedy gets right answer
If you move from your current position cur to another position nxt then It should be a[nxt]>a[cur], else it's optimal to stay at your current position.
I hope you understand.
Yeah I get it now. I was stuck on dp approach making it complex and wasn't able to think greedy.
Thanks
第四题出的太好了
For G2 there is also solution using the problem:
-we can deactivate an element
-we need to find the closest active element to the right
That can be done using dsu
Then we'll increase lcp. When we increase it by one, we deactivate elements, so we're left only with elements with $$$z_i \ge curLCP$$$ where $$$z_i$$$ is z-function.
To find maximum $$$k$$$ that can achieve at least $$$curLCP$$$ we will start at the beginning and then jump to the next active element of $$$i + curLCP$$$. Since the answer for $$$curLCP$$$ is at most $$$\frac{n}{curLCP}$$$, $$$O(ans)$$$ solution works in $$$O(n log n)$$$, and dsu gives us either $$$\alpha(n)$$$ or $$$log n$$$
Interesting solution, do you have the code example?
259187296 for example
What's nice about this task is that there so many different interesting solutions
https://codeforces.me/contest/1968/submission/259227872
In G2, shouldn't the time complexity of the case when $$$k > \sqrt{n}$$$ be $$$\mathcal{O}(n \sqrt{n})$$$? (the editorial says it's $$$\mathcal{O}(n \sqrt{n} \log{n})$$$)
I agree. The total complexity is ($$$n\sqrt{n}\ logn$$$), but when $$$k>n$$$,it works in ($$$n\sqrt{n}$$$).
Thanks, fixed:)
approx. rating of G2? 2100+ right?
clist said 2266 as I typed this.
That usually means 2000-2100
For G2 I had a similar idea to use the fact that the answer only changes a few times and I calculated the answer for each segment with new n/l.
However, this got WA, not sure why, so I replaced it with an O(n*log^2(n)) (please someone correct me if I'm wrong).
You first binary search for the leftmost index with an answer less than the last one.
Here's the submission 259255876
It TLE'd on the general test. :(
shouldn't O(N log^2 (N)) <= O(N sqrt(N))
I'll try analyzing the complexity and if someone can correct me...
1- Calculating the Z function is done in O(N)
2- Then there's the check which is also O(N)
3- Both binary searches are log(N)
4- is there a sqrt(N) I'm missing maybe?
I also TLED first. But I added a new array to store the values. So to reduce calculating values for given x more than once. This essentially ACED
My friend had an $$$O(n \log^2{n})$$$ solution that ACed (which I believe uses a similar idea to your $$$n/l$$$ thing), if you wanna check that out.
I don't quite understand tbh. if you could explain it to me please... unforgettablepl
In my code, the calc function is pretty much the same as the check function in your code. The got variable in your code stores the maximal k such that the answer is >= len. In my code, the calc function returns the got variable. Now I make an array called ans where ans[i] = maximal k such that the answer is >= i using this function. For answering queries I just binary search over this answer array.
Use hash to check whether two string equal again.
And be hacked again (((
I used hashing too, but I wasn't hacked since I used mersenne twister to randomly select mod for hashing.
Can you share your hashing template?
Here you go.
Also be aware that the function isPal only works if the to the string is appended its reverse.
For example, let's say we will call isPal for the string s = "cabad".
To chech is substring from "aba" is palindrome, you have to initialize the hashing structure with the string "cabaddabac"
Does this line returns a prime number?
ll mod = uniform_int_distribution<int>((int)(1e9+7), (int)(1e9+1e8))(rng);No. It return random integer in the range $$$[10^9+7, 1.1*10^9]$$$.
The mod doesn't need to be a prime number.
Thank you my friend.
Why such tight constraints on G2, $$$n \leq 2\cdot 10^5$$$ when the intended time complexity is $$$O(n\sqrt{n}log(n))$$$??
There is (in my opinion) easier $$$O(n log^{2}n)$$$ solutions too.
Hey,
G2 is solvable in O(NlogNlogN): checking the maximum number of intervals one can separate in such that the common prefix has length at least k is doable in O(N/k logN) if we store the valid indices with Z[i]>=k in a set.
Can someone understand why the solution to F gives TLE if we use unordered_map<int,vector > instead of map<int,vector >? My solution using unordered_map was TLEd in the main tests, and the official solution has the same issue when we use unordered_map. This seems unintuitive as we never use the key ordering.
Thanks!
For the 2nd point, I think even from the main tests have some exploits on unordered_map to cause enough hash collisions for $$$\mathcal{O}(n)$$$ access. It's been a common exploit for quite a while, and it's due to hash table's nature itself, as long as its hashing could be reverse engineered.
Thanks!
now I get it
Is there any tutorial for that Z function used in G1?
Edu
Is it this? https://cp-algorithms.com/string/z-function.html
Can anyone refer me more problems like E?
Check out constructive algorithms
of what range?
Range? I’m not sure what you mean.
Problem rating like 1600-1700?
There’s a wide range of difficulty for constructive algorithms, so I’m not sure what to suggest. Just choose the difficulty range you would normally do, I suppose?
Okay, sure Btw thanks
why do we usually use a segment tree for finding xor on segments and not just how it was described in the problem f? or we just do this only when elements don't change?
Correct. We can do prefix XOR to evaluate range XOR in case that there are no updates (That is, no change). But if there are updates, then we use a Fenwick or segment tree.
how can we use segment tree pls tell??
In the same way how it is used for sums, but you change each node to store the XOR of the interval instead.
ohk got it, thanks
I think there's an error in the editorial for problem F. It says "we may find the largest t <= r" but it should be t < r since if t == r then the segment [t+1, r] would not make sense. I tried a solution with this change in mind and it got AC. 259369531
Looks like I have to practice more to recognize patterns in problems like in E!
For Problem C, if we want to find the lexicographically smallest sequence $$$a_1, a_2, a_3, ..., a_n$$$ what would be the approach?
Anyone has an idea why this one gets TLE https://codeforces.me/contest/1968/submission/259216131 ? it is exactly the same complexity as the editorial solution.
On problem F i am not convinced with the solution , can anyone provide with a better approach here , because i see the statement that
Observation: any division on more than k>3 segments can be reduced to at most 3 segments. Doesn't hold the biequivalence , that if the segment can be divided into atmost 3 segments then it can be divided into k segments
The equivalence is not needed, we simply require that k > 1.
We are only required to show an injection in one direction. I think we can't show bijection here, because it is not always true, that we may divide from $$$3$$$ segments up to $$$k$$$.
Easy observation solution for E. Put two dots at (1,1) and (n,n) One dot at (2,1). and the remaining(n-3) on the first row starting from the third column. The intuition behind this is to get all possible Distances for N >= 4. To get all distance I first choose (1,1) and (n,n) which gives distances 0 and 2*n-2. then put one at (1,2) to get the distance of 1 and 2*n-1. We can get the remaining in pairs if we put them on the first row. for ex- (1,3) will give distance 2 and 2*n. and so on for (1,4), (1,5) ... .
could someone please explain the bfs solution for problem D, also what will be maximum number of steps to reach a cycle in a permutation of length n where we move from a random number x in permutation to permutation[x] 1 indexing similalry moving forward
In a permutation of length n, the max number of steps to reach a cycle is always n.
example : 4 3 1 2
Here, whatever starting position you had, you will need to perform 4 moves to end up at the starting position
for 3 2 1 and if you are at 3 you go to p(3) that is 1 and then p(1) that is 3 it took only two steps right
I have a general doubt, on how to build a constructive approach + thinking in problems like E. I generally find it difficult to find a pattern. So in general what should be my approach while tackling such problems. (Ig having the right intuition at the beginning is very important.) If possible please do suggest me something on this :)
(Disclaimer) I haven't solved E since lack of time. I think everyone has it since there is no generalisation in such problems :) What I find helpful for myself is to look into the properties of data structures and operations used in problems. For example, it's clear u can get max Manhattan distance by putting cells into corners. It gives u unique combination and also a range of all possible distances. Than u can see, that putting cells into the lines/diagonals gives u lots of other combinations since u have more unique values in the formula. The hardest part is to notice that u lack some values in the range and how to adjust it. I would say that examples in the problem allow u to reverse engineer the idea of leaving one empty column and putting 2 cells into one.
Another example is a task C where solution based on one property of modular arithmetic. Tutorial used one property, I used similar one (a mod b = a b > a), which allowed me to take as ai just xi if condition is satisfied and if not i still took ai as xi only with an adjustment of ai-1 by ai-2 as many times as needed.
problem E as per the tutorial: Interesting fact, that in such way we generate all possible Manhattan distances. Odd distances are generated between cells from the main diagonal and (n−1,n). Even distances are generated between cells from the main diagonal and (n,n)
but I guess if total x manhattan distances exist then we only get x-1 , how to prove we can get max x-1 distances only ?
if I am wrong please correct me
JuicyGrape Please help !!
ohh I understand, we get all the distances both even and odd except in the case of 2,3.
Could you please explain the idea behind problem E solution? I am not quite sure
First, try to find all possible distances, Try to put all the pieces diagonally, see what distances are covered, and then what happens if you move a piece. What distances are covered now?
There are other ways like placing in the first row and last column, you can try to find these patterns also.
we have only a single clue what distances we can cover, and if all, then how? If not, how do you cover max number of distances?
Thanks. Got it :)
In problem F, what is wrong in the following logic: (Here a represents the prefix xor array and mp is mp[xor] = vector)
You need to look for the sum
a[l - 1], not0.The result of the second call to
lower_bound()may not be dereferenceable.You don't have to check whether $$$y>x$$$ or $$$x\ge l$$$, since these things are automatically true.
Why is O(nlogn) approach exceeding time limit in B question? Normally O(nlogn) works with n<2x10^5 and time limit = 2 sec.
(i tried to write a solution using upper bound 259169919)
You are using
upper_boundincorrectly: the waysetis structured isn't linear, thus it will make your command $$$\mathcal{O}(n)$$$.Instead, use the class method built for
set, something like this:auto x1 = ons.upper_bound(lst);auto x2 = zrs.upper_bound(lst);thanks for the help
How else can G1 be solved ?
Binary Search on Prefiquence felt more intuitive. https://codeforces.me/contest/1968/submission/259543727
Could someone tell me what is wrong with my submission https://codeforces.me/contest/1968/submission/259550793
are there any problems similar to F
Can someone please explain to me the solution for problem D cause, I can't understand the editorial clearly
Let me explain my idea:
Let $$$f_s(p)$$$ be the total score of a player when he starts at the position $$$s$$$, always moves from his current position until he reaches $$$p$$$, and after reaching $$$p$$$, always stays at his current position. Bodya and Sasha's maximum score will be $$$\max_{1 \le i \le n}{f_{P_B}(i)}$$$ and $$$\max_{1 \le i \le n}{f_{P_S}(i)}$$$ respectively.
This claim is correct because, a player will always move from his current position only when there lies some better position with higher $$$a_x$$$, somewhere in the future along the path of his $$$k$$$ moves. Now we will prove why it is always better for him to move now instead of staying at the current position for some turns and then move.
If his current position is $$$x$$$, and he decides to stay at $$$x$$$ for some (one or more) turns, and then move to $$$p_x$$$, there are the following three cases:
So the optimal move for a player will be — some number of moves (possibly zero), followed by some number of stays (possibly zero), until he completes his $$$k$$$ turns. So we basically iterate over his final position to know the maximum possible score.
For all $$$1 \le i \le n$$$, $$$f_s(i)$$$ can be calculated in $$$O(n)$$$ by keeping track of how many turns it takes to reach $$$i$$$ starting at $$$s$$$ and the total score obtained along the path.
So overall running time of the solution is $$$O(n)$$$.
You can check my submission for better understanding: 259185280.
Thank you for your explanation
Why my solution is failing for G1? I have used the same idea stated in the editorial but instead of z-function, I have used rolling-hash. My Code
About the problem F , I have a question. According to the formula $$$X ^ X ^ X = X$$$ , why reduce k to three , instead of further reduce one? Could help me ?
$$$one$$$ subarray is not allowed in the problem.
Thank you for your reply! I actually forget the detail , $$$k > 1$$$.
I implemented the solution described by the editorial for G2 during contest but got TLE...
https://codeforces.me/contest/1968/submission/259238179
I am posting this so late because I was trying to upsolve with a smarter solution, but couldn't come up with one. It's pretty frustrating that my approach was correct but failed because of the constant factor.
for f what is the different between "--lower_bound(id[a[l-1]].begin(),id[a[l-1]].end(),r)" and "lower_bound(id[a[l-1]].begin(),id[a[l-1]].end(),r — 1)"
You don't find lower_bound $$$>=$$$ in the first case instead you find the first value that is $$$<$$$ $$$r$$$
thx bro
I don't get why simple binary search doesn't work on G1. Can anyone explain? Why my code gets WA on 3 test? https://pastebin.com/SnQmt9qk
problem D was awesome.
can you suggest more problems like that one?!
Good tutorial, thanks! But I want to ask that In problem F, why we should do mp[0].push_back(0) ?
For G2: I would be glad if any one help understand why author's O(n√n log(n) ) solution is passing where n=2e5 and time limit 3s.
Can somebody help me with Problem D submission ? i seem stuck here. 260790899
Can someone please tell what mistake am I doing in G1 ?
https://codeforces.me/contest/1968/submission/260861542
G2 卡常 厳しすぎ!! (Constant factor for G2 too tight!)
I implemented the solution described in the editorial, with KMP instead of Z-function, but all my submissions ended up TLE41 (261016696) and I couldn't get the log^2 solution right.
By dividing the submission into $$$>\sqrt{n}$$$ and $$$\le\sqrt{n}$$$ parts I found my solution would finish in 3.2 seconds and I tried my best to squeeze in but still couldn't.
Could anyone help me optimize the constant factor further, or is KMP unable to pass?
BTW I don't think a $$$2e5$$$ data range for a $$$O(n\sqrt{n}\log n)$$$ intended solution is quite appropriate.
if we divide the first part into < root(N / log(N)) and > root(N * log(N)) we can have a time complexity of n * root(n * log(n)). Maybe you can try this.
In G2 I submitted 2 solutions one wit time complexity O(N * sqrt(N) * log(n)) and other with O(N * sqrt(N * log(N))). The former solution passed whereas the later gave TLE. Does anyone have any idea why this is happening?
Former solution: https://codeforces.me/contest/1968/submission/261653053
Latter solution: https://codeforces.me/contest/1968/submission/261652536
what is the need of permutation in the problem D
E was too easy to be E
hi i have employed pretty much same logic as given in editorial in problem C , but in reverse sense but it is not giving right output for last test case (1 5) can u help what is wrong with it
any idea why does this get tle?
https://codeforces.me/contest/1968/submission/268508103
G2 can be easily solved with z-function in O(nlogn^2). We find the maximal k for each answer i in increasing order. Use ordered set to maintain list of all indices in z-function that are greater than or equal to i and binary search for each next index. This allows us to binary search for each answer. Code
in problem F's code, how come you don't check whether the lower_bound iterator points to the begin() before decrementing it? Is there some guarantee in the problem I'm missing?