| Codeforces Round 813 (Div. 2) |
|---|
| Закончено |
Массив из $$$n$$$ целых положительных чисел $$$a_1,a_2,\ldots,a_n$$$ упал на вас с небес вместе с целым положительным числом $$$k \le n$$$.
Вы можете применить следующую операцию не более $$$k$$$ раз:
- Выбрать индекс $$$1 \le i \le n$$$ и целое число $$$1 \le x \le 10^9$$$. Затем выполнить $$$a_i := x$$$ (присвоить $$$x$$$ значению $$$a_i$$$).
Затем вы строите полный неориентированный взвешенный граф с $$$n$$$ вершинами, пронумерованными целыми числами от $$$1$$$ до $$$n$$$, где ребро $$$(l, r)$$$ ($$$1 \le l < r \le n$$$) имеет вес $$$\min(a_{l},a_{l+1},\ldots,a_{r})$$$.
Вам необходимо найти максимально возможный диаметр итогового графа после применения не более $$$k$$$ операций.
Диаметр неориентированного взвешенного графа равен $$$\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$$$, где $$$\operatorname{d}(u, v)$$$ является длиной кратчайшего пути между вершинами $$$u$$$ и $$$v$$$ данного графа.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 10^5$$$, $$$1 \le k \le n$$$).
Вторая строка каждого набора входных данных содержит $$$n$$$ целых положительных чисел $$$a_1,a_2,\ldots,a_n$$$ ($$$1 \le a_i \le 10^9$$$).
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите единственное целое число — максимально возможный диаметр итогового графа после применения не более $$$k$$$ операций.
63 12 4 13 21 9 843 110 2 63 2179 17 10000000002 15 92 24 2
4 168 10 1000000000 9 1000000000
В первом наборе входных данных один из оптимальных итоговых массивов — $$$[2,4,5]$$$.
Граф, полученный из данного массива:
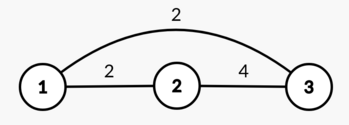
$$$\operatorname{d}(1, 2) = \operatorname{d}(1, 3) = 2$$$ и $$$\operatorname{d}(2, 3) = 4$$$, поэтому диаметр графа равен $$$\max(2,2,4) = 4$$$.
| Название |
|---|




