| Codeforces Round 813 (Div. 2) |
|---|
| Finished |
An array of $$$n$$$ positive integers $$$a_1,a_2,\ldots,a_n$$$ fell down on you from the skies, along with a positive integer $$$k \le n$$$.
You can apply the following operation at most $$$k$$$ times:
- Choose an index $$$1 \le i \le n$$$ and an integer $$$1 \le x \le 10^9$$$. Then do $$$a_i := x$$$ (assign $$$x$$$ to $$$a_i$$$).
Then build a complete undirected weighted graph with $$$n$$$ vertices numbered with integers from $$$1$$$ to $$$n$$$, where edge $$$(l, r)$$$ ($$$1 \le l < r \le n$$$) has weight $$$\min(a_{l},a_{l+1},\ldots,a_{r})$$$.
You have to find the maximum possible diameter of the resulting graph after performing at most $$$k$$$ operations.
The diameter of a graph is equal to $$$\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$$$, where $$$\operatorname{d}(u, v)$$$ is the length of the shortest path between vertex $$$u$$$ and vertex $$$v$$$.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^4$$$). Description of the test cases follows.
The first line of each test case contains two integers $$$n$$$ and $$$k$$$ ($$$2 \le n \le 10^5$$$, $$$1 \le k \le n$$$).
The second line of each test case contains $$$n$$$ positive integers $$$a_1,a_2,\ldots,a_n$$$ ($$$1 \le a_i \le 10^9$$$).
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$10^5$$$.
For each test case print one integer — the maximum possible diameter of the graph after performing at most $$$k$$$ operations.
63 12 4 13 21 9 843 110 2 63 2179 17 10000000002 15 92 24 2
4 168 10 1000000000 9 1000000000
In the first test case, one of the optimal arrays is $$$[2,4,5]$$$.
The graph built on this array:
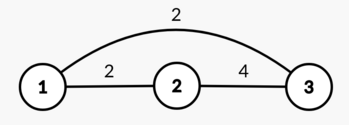
$$$\operatorname{d}(1, 2) = \operatorname{d}(1, 3) = 2$$$ and $$$\operatorname{d}(2, 3) = 4$$$, so the diameter is equal to $$$\max(2,2,4) = 4$$$.
| Name |
|---|




