| Codeforces Round 655 (Div. 2) |
|---|
| Закончено |
Омкар строит дом. Он хочет решить, как составить план пола на последнем этаже.
Пол Омкара изначально выглядит как $$$n$$$ строк по $$$m$$$ нолей. ($$$1 \le n,m \le 100$$$). Каждая строка разделена на отрезки, причем каждый $$$0$$$ в строке находится ровно в $$$1$$$ отрезке. Для каждого отрезка для каждой строки Омкар может заменить ровно один из $$$0$$$, содержащихся в этом отрезке, на $$$1$$$. Омкар определяет качество пола как сумму квадратов сумм значений в каждом столбце, т.е. если сумма значений в $$$i$$$-м столбце равна $$$q_i$$$, то качество пола равно $$$\sum_{i = 1}^m q_i^2$$$.
Помогите Омкару найти максимальное качество, которое может иметь пол.
Первая строка содержит два целых числа, $$$n$$$ и $$$m$$$ ($$$1 \le n,m \le 100$$$), которые являются количеством строк и количеством столбцов соответственно.
Затем вы получите описание отрезков в каждой строке. Для каждой строки $$$i$$$ от $$$1$$$ до $$$n$$$: Первая строка содержит одно целое число $$$k_i$$$ ($$$1 \le k_i \le m$$$) — которое является количеством отрезков в строке $$$i$$$. $$$j$$$-я из следующих $$$k_i$$$ строк содержит два целых числа $$$l_{i,j}$$$ и $$$r_{i,j}$$$, которые являются левой и правой границей (обе включительно), соответственно, $$$j$$$-го отрезка $$$i$$$-й строки. Гарантируется, что $$$l_{i,1} = 1$$$, $$$l_{i,j} \leq r_{i,j}$$$ для всех $$$1 \le j \le k_i$$$, $$$r_{i,j-1} + 1 = l_{i,j}$$$ для всех $$$2 \le j \le k_i$$$, и $$$r_{i,k_i} = m$$$.
Выведите одно целое число, которое является максимально возможным качеством пола.
4 5 2 1 2 3 5 2 1 3 4 5 3 1 1 2 4 5 5 3 1 1 2 2 3 5
36
Данный пример соответствует следующей диаграмме. Ячейки в одном ряду с одинаковым номером являются частью одного и того же отрезка.
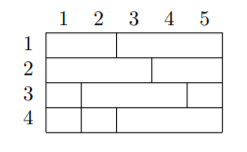
Наиболее оптимальным планом является:
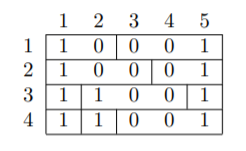
Сумма $$$1$$$-го столбца равна $$$4$$$, сумма $$$2$$$-го столбца равна $$$2$$$, сумма $$$3$$$-го и $$$4$$$-го столбцов равна $$$0$$$, а сумма $$$5$$$-го столбца равна $$$4$$$.
Качество этого плана этажа составляет $$$4^2 + 2^2 + 0^2 + 0^2 + 4^2 = 36$$$. Можно показать, что нет плана пола с более высоким качеством.
| Название |
|---|




