| Codeforces Round 621 (Div. 1 + Div. 2) |
|---|
| Закончено |
Бесси пасется на ферме, состоящей из $$$n$$$ полей, соединенных с помощью $$$m$$$ двусторонних дорог. Сейчас она находится на поле $$$1$$$, и вернется домой на поле $$$n$$$ в конце дня.
Кор-федерация Коровников приказала Фермеру Джону построить одну дополнительную двустороннюю дорогу. У фермы есть $$$k$$$ особых полей, и было решено построить дорогу между двумя различными особыми полями. Фермер Джон может построить дорогу даже между полями, которые уже соединены дорогой.
Уже после постройки дороги, Бесси вернется по кратчайшему пути от поля $$$1$$$ к полю $$$n$$$. Так как Бесси нужно больше тренироваться, Фермер Джон должен максимизировать длину данного кратчайшего пути. Помогите ему!
В первой строке заданы три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$n-1 \le m \le 2 \cdot 10^5$$$, $$$2 \le k \le n$$$) — количество полей на ферме, количество дорог и количество особых полей.
Во второй строке заданы $$$k$$$ целых чисел $$$a_1, a_2, \ldots, a_k$$$ ($$$1 \le a_i \le n$$$) — номера особых полей. Все $$$a_i$$$ различны.
В $$$i$$$-й из следующих $$$m$$$ строк задано два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$, $$$x_i \ne y_i$$$), описывающих двустороннюю дорогу между полями $$$x_i$$$ и $$$y_i$$$.
Гарантируется, что из любого поля можно добраться до любого другого поля. Также гарантируется, что для любой пары полей существует не более одной дороги, непосредственно соединяющей их.
Выведите единственное число — максимально возможную длину кратчайшего пути из $$$1$$$ в $$$n$$$ после того, как Фермер Джон построит одну дорогу оптимально.
5 5 3 1 3 5 1 2 2 3 3 4 3 5 2 4
3
5 4 2 2 4 1 2 2 3 3 4 4 5
3
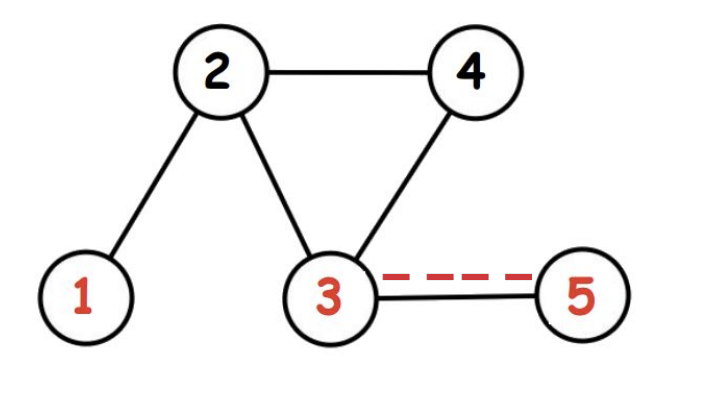
Граф из первого примера изображен ниже. Особые поля отмечены красным. Для Фермера Джона оптимально построить дорогу между полями $$$3$$$ и $$$5$$$, тогда кратчайший путь из $$$1$$$ в $$$5$$$ будет равен $$$3$$$.
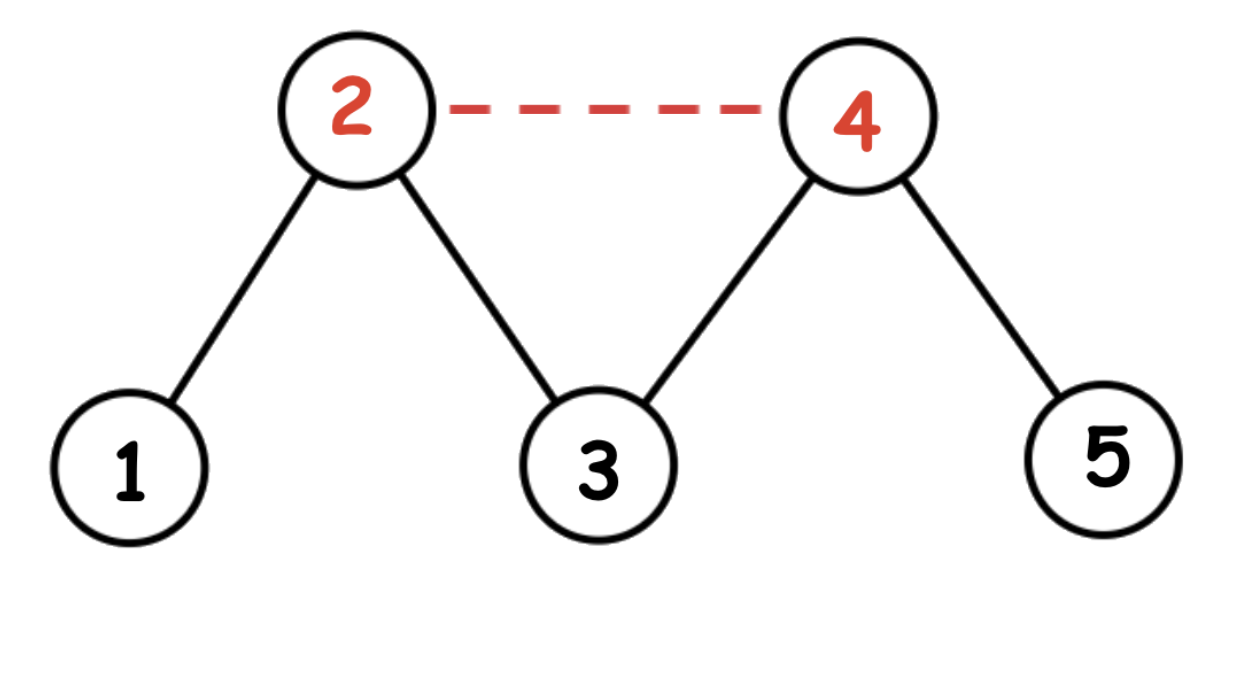
Граф из второго примера изображен ниже. Фермер Джон должен построить дорогу между полями $$$2$$$ и $$$4$$$, тогда кратчайший путь из $$$1$$$ в $$$5$$$ будет равен $$$3$$$.
| Название |
|---|




