Idea: FieryPhoenix
Tutorial
Tutorial is loading...
Solution
#include <iostream>
using namespace std;
int N,D,a[105];
int main(){
int T; cin>>T;
while (T--){
cin>>N>>D;
for (int i=1;i<=N;i++)
cin>>a[i];
while (D--){ //loop over D days
for (int i=2;i<=N;i++)
if (a[i]>0){ //move closest haybale over
a[i]--;
a[i-1]++;
break;
}
}
cout<<a[1]<<endl;
}
}
Alternative O(n) Solution:
#include <iostream>
using namespace std;
int N,D,a[105],ans;
int main(){
int T; cin>>T;
while (T--){
cin>>N>>D;
for (int i=1;i<=N;i++)
cin>>a[i];
for (int i=2;i<=N;i++){
int move=min(a[i],D/(i-1)); //number of haybales we can move from pile i to pile 1
a[1]+=move; //update pile 1
D-=move*(i-1); //update remaining days
}
cout<<a[1]<<endl;
}
}
Idea: dragonslayerintraining
Tutorial
Tutorial is loading...
Solution
#include <iostream>
#include <set>
#include <algorithm>
using namespace std;
set<int>a;
//you don't have to use set, it was just easier for us
int main(){
int T; cin>>T;
while (T--){
int N,X;
cin>>N>>X;
int far=0; //largest favorite number
for (int i=0;i<N;i++){
int A;
cin>>A;
a.insert(A);
far=max(far,A);
}
if (a.count(X)) //X is favorite number
cout<<1<<endl;
else
cout<<max(2,(X+far-1)/far)<<endl; //expression as explained in tutorial
a.clear();
}
}
Idea: dragonslayerintraining
Tutorial
Tutorial is loading...
Solution
#include <iostream>
using namespace std;
typedef long long ll;
ll arr1[26],arr2[26][26];
int main(){
string S;
cin>>S;
for (int i=0;i<S.length();i++){
int c=S[i]-'a';
for (int j=0;j<26;j++)
arr2[j][c]+=arr1[j];
arr1[c]++;
}
ll ans=0;
for (int i=0;i<26;i++)
ans=max(ans,arr1[i]);
for (int i=0;i<26;i++)
for (int j=0;j<26;j++)
ans=max(ans,arr2[i][j]);
cout<<ans<<endl;
}
Idea: FieryPhoenix
Tutorial
Tutorial is loading...
Solution
#include <cstdio>
#include <vector>
#include <algorithm>
const int INF=1e9+7;
int N;
int as[200005];
std::vector<int> edges[200005];
int dist[2][200005];
int q[200005];
void bfs(int* dist,int s){
std::fill(dist,dist+N,INF);
int qh=0,qt=0;
q[qh++]=s;
dist[s]=0;
while(qt<qh){
int x=q[qt++];
for(int y:edges[x]){
if(dist[y]==INF){
dist[y]=dist[x]+1;
q[qh++]=y;
}
}
}
}
int main(){
int M,K;
scanf("%d %d %d",&N,&M,&K);
for(int i=0;i<K;i++){
scanf("%d",&as[i]);
as[i]--;
}
std::sort(as,as+K);
for(int i=0;i<M;i++){
int X,Y;
scanf("%d %d",&X,&Y);
X--,Y--;
edges[X].push_back(Y);
edges[Y].push_back(X);
}
bfs(dist[0],0);
bfs(dist[1],N-1);
std::vector<std::pair<int,int> > data;
for(int i=0;i<K;i++){
data.emplace_back(dist[0][as[i]]-dist[1][as[i]],as[i]);
}
std::sort(data.begin(),data.end());
int best=0;
int max=-INF;
for(auto it:data){
int a=it.second;
best=std::max(best,max+dist[1][a]);
max=std::max(max,dist[0][a]);
}
printf("%d\n",std::min(dist[0][N-1],best+1));
}
Idea: FieryPhoenix
Tutorial
Tutorial is loading...
Solution
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cassert>
const int MOD=1e9+7;
int modexp(int base,int exp){
int ac=1;
for(;exp;exp>>=1){
if(exp&1) ac=1LL*ac*base%MOD;
base=1LL*base*base%MOD;
}
return ac;
}
int inverse(int x){
return modexp(x,MOD-2);
}
int fs[100005];
int left[100005],right[100005];
std::vector<int> cows[100005];//cows[f]: hunger of cows that like flavor f
int asleep[100005];
int ways[100005];
int total_asleep=0,total_ways=1;
void calc_ways(int f){
int a=std::upper_bound(cows[f].begin(),cows[f].end(),left[f])-cows[f].begin();
int b=std::upper_bound(cows[f].begin(),cows[f].end(),right[f])-cows[f].begin();
if(a>b) std::swap(a,b);
long long cnt2=1LL*a*b-a;
int cnt1=a+b;
cnt2%=MOD;
if(cnt2>0){
asleep[f]=2;
ways[f]=cnt2;
}else if(cnt1>0){
asleep[f]=1;
ways[f]=cnt1;
}else{
asleep[f]=0;
ways[f]=1;
}
}
//fixed left cow, with hunger left[i]
//precondition: such cow exists
void calc_ways_stuck(int f){
int b=std::upper_bound(cows[f].begin(),cows[f].end(),right[f])-cows[f].begin();
if(right[f]>=left[f])
b--;
int cnt2=b;
if(cnt2>0){
asleep[f]=2;
ways[f]=cnt2;
}else{
asleep[f]=1;
ways[f]=1;
}
}
int ans_asleep=0,ans_ways=0;
void add_to_ans(int asleep,int ways){
if(asleep>ans_asleep){
ans_asleep=asleep;
ans_ways=0;
}
if(asleep==ans_asleep)
ans_ways=(ans_ways+ways)%MOD;
}
int main(){
int N,M;
scanf("%d %d",&N,&M);
for(int i=1;i<=N;i++){
scanf("%d",&fs[i]);
right[fs[i]]++;
}
for(int i=0;i<M;i++){
int F,H;
scanf("%d %d",&F,&H);
cows[F].push_back(H);
}
for(int f=1;f<=N;f++)
std::sort(cows[f].begin(),cows[f].end());
for(int f=1;f<=N;f++){
calc_ways(f);
total_asleep+=asleep[f];
total_ways=1LL*total_ways*ways[f]%MOD;
}
add_to_ans(total_asleep,total_ways);
for(int i=1;i<=N;i++){
total_asleep-=asleep[fs[i]];
total_ways=1LL*total_ways*inverse(ways[fs[i]])%MOD;
right[fs[i]]--;
left[fs[i]]++;
if(std::binary_search(cows[fs[i]].begin(),cows[fs[i]].end(),left[fs[i]])){
calc_ways_stuck(fs[i]);
int here_asleep=total_asleep+asleep[fs[i]];
int here_ways=1LL*total_ways*ways[fs[i]]%MOD;
add_to_ans(here_asleep,here_ways);
}
calc_ways(fs[i]);
total_asleep+=asleep[fs[i]];
total_ways=1LL*total_ways*ways[fs[i]]%MOD;
}
printf("%d %d\n",ans_asleep,ans_ways);
}
Idea: FieryPhoenix
Tutorial
Tutorial is loading...
Solution
#include <cstdio>
#include <vector>
#include <cassert>
#include <queue>
#include <algorithm>
const int INF=1e9+7;
std::vector<int> edges[400005];
int anc[19][400005];
int depth[400005];
void dfs(int node){
for(int child:edges[node]){
edges[child].erase(std::find(edges[child].begin(),edges[child].end(),node));
anc[0][child]=node;
for(int k=1;k<19;k++){
anc[k][child]=anc[k-1][anc[k-1][child]];
}
depth[child]=depth[node]+1;
dfs(child);
}
}
int la(int node,int len){
for(int k=19-1;k>=0;k--){
if(len&(1<<k)){
node=anc[k][node];
}
}
return node;
}
int lca(int a,int b){
if(depth[a]<depth[b]) std::swap(a,b);
a=la(a,depth[a]-depth[b]);
if(a==b) return a;
for(int k=19-1;k>=0;k--){
if(anc[k][a]!=anc[k][b]){
a=anc[k][a];
b=anc[k][b];
}
}
return anc[0][a];
}
//move x steps from a to b
//assumes x<=dist(a,b)
int walk(int a,int b,int x){
int c=lca(a,b);
if(x<=depth[a]-depth[c]){
return la(a,x);
}
int excess=x-(depth[a]-depth[c]);
assert(excess<=(depth[b]-depth[c]));
return la(b,depth[b]-depth[c]-excess);
}
int uf[400005];
int dist[400005];//dist[x]=0 iff x is rest stop
int find(int a){
while(a!=uf[a]){
a=uf[a]=uf[uf[a]];
}
return a;
}
bool query(int K){
int A,B;
scanf("%d %d",&A,&B);
A--,B--;
int C=lca(A,B);
if(depth[A]+depth[B]-2*depth[C]<=2*K){
return true;
}else{
return find(walk(A,B,K))==find(walk(B,A,K));
}
}
int main(){
int N,K,R;
scanf("%d %d %d",&N,&K,&R);
int oldN=N;
for(int i=0;i<oldN-1;i++){
int X,Y;
scanf("%d %d",&X,&Y);
X--,Y--;
edges[X].push_back(N);
edges[N].push_back(X);
edges[Y].push_back(N);
edges[N].push_back(Y);
N++;
}
for(int i=0;i<N;i++){
uf[i]=i;
}
std::fill(dist,dist+N,INF);
std::queue<int> frontier;
for(int i=0;i<R;i++){
int X;
scanf("%d",&X);
X--;
dist[X]=0;
frontier.push(X);
}
while(!frontier.empty()){
int x=frontier.front();
if(dist[x]>K-1) break;
frontier.pop();
for(int y:edges[x]){
uf[find(y)]=find(x);
if(dist[y]==INF){
dist[y]=dist[x]+1;
frontier.push(y);
}
}
}
dfs(0);
int V;
scanf("%d",&V);
while(V--){
if(query(K)){
printf("YES\n");
}else{
printf("NO\n");
}
}
}
Idea: dragonslayerintraining
Tutorial
Tutorial is loading...
Solution
#include <cstdio>
#include <queue>
#include <vector>
#include <stdint.h>
#include <algorithm>
const long long INF=1e9+7;
const long long MAXV=50;
const long long MAXE=MAXV*(MAXV-1);
long long SRC,SNK;
long long elist[MAXE*2];
long long next[MAXE*2];
long long head[MAXV];
long long cap[MAXE*2];
long long cost[MAXE*2];
long long tot=0;
void add(long long x,long long c,long long w){
elist[tot]=x;
cap[tot]=c;
cost[tot]=w;
next[tot]=head[x];
head[x]=tot++;
}
long long dist[MAXV];
long long prev[MAXV];
std::queue<long long> q;
long long total_cost=0;
long long total_flow=0;
int main(){
long long N,M;
scanf("%lld %lld",&N,&M);
SRC=0,SNK=N-1;
std::fill(head,head+N,-1);
for(long long i=0;i<M;i++){
long long A,B,C;
scanf("%lld %lld %lld",&A,&B,&C);
A--,B--;
add(A,1,C);
add(B,0,-C);
}
std::vector<std::pair<long long,long long> > crit;
crit.push_back({0,0});
while(true){
std::fill(dist,dist+N,INF);
dist[SRC]=0;
prev[SRC]=-1;
q.push(SRC);
while(!q.empty()){
long long node=q.front();
q.pop();
for(long long e=head[node];e!=-1;e=next[e]){
long long i=elist[e^1];
if(cap[e]){
if(dist[i]>dist[node]+cost[e]){
dist[i]=dist[node]+cost[e];
prev[i]=e;
q.push(i);
}
}
}
}
crit.push_back({1LL*total_flow*dist[SNK]-total_cost,dist[SNK]});
if(dist[SNK]==INF) break;
long long aug=INF;
for(long long x=SNK;x!=SRC;x=elist[prev[x]]){
aug=std::min(aug,cap[prev[x]]);
}
for(long long x=SNK;x!=SRC;x=elist[prev[x]]){
cap[prev[x]]-=aug;
cap[prev[x]^1]+=aug;
}
total_flow+=aug;
total_cost+=1LL*dist[SNK]*aug;
}
long long Q;
scanf("%lld",&Q);
while(Q--){
long long X;
scanf("%lld",&X);
auto it=std::lower_bound(crit.begin(),crit.end(),std::pair<long long,long long>{X+1,0});
double D=(long double)((X-(it-1)->first)*it->second+(it->first-X)*((it-1)->second))/(it->first-(it-1)->first);
printf("%.10lf\n",D);
}
return 0;
}










wonderful problems and nice contest
Test Case 7 of C?
probably something like aaaa (where the answer is 6 because aa occurs at (1,2),(1,3),(1,4),(2,3),(2,4),(3,4)), at least I also failed pretest 7 and was told afterwards that not covering this case was my error
case of 2 same letters I suppose, because I fixed that and got AC
I think it's 1e5 aaaa..... I got WA on Test 7 fixed after changing int to long long
it is 100000 'j' and all other 0. so u might have missed the cases in which 2 'j' are there in AP. it will be nC2 == n*(n-1)/2 . then u will get AC in it.
G already appeared many times. This is at least third time I see this. Fortunately first one where I get it accepted (at least on pretests), but I still have no idea what the solution is, I copied Marcin_smu's code from Petrozavodsk (Winter 2016 problem J2) and made some adjustments :P. It appeared on some Topcoder as well, but I couldn't find it (iirc setter was Lewin)
I wasn’t able to solve this version :(
I think you might be referring to this problem: https://community.topcoder.com/stat?c=problem_statement&pm=13952. It’s a bit different though, and has a bound on number of edges which makes it a bit easier.
During the contest I had the following solution for F:
Do centroid decomposition. Each query will be solved at its centroid.
For each node and depth in the centroid tree, I compute $$$up(node)$$$ being the special node that can be reached by going up as few edges as possible, making at most $$$k$$$ moves, and with a lower depth than $$$node$$$ (closer to the root). Then I computed $$$dp(node)$$$ the "closest" you can get to the centroid via special nodes with the formula $$$dp(node) = min(depth(node), dp(up(node)))$$$.
To solve a query we just check that $$$dp(a) + dp(b) \leq k$$$.
However, this gives incorrect on test 10. Do you have a counter-example?
Code: https://pastebin.com/62MjcNeL
To solve a query you assume that you just have to check the inequality on the centroid that is $$$lca(a, b)$$$ but this is not sufficient.
In this test, the very first centroid is the only rest stop.
EDIT: The first line of the test was not visible.
Your test seems to be missing one edge. Could you please be more specific? I don't understand what you mean in your comment.
At line 42 you find
cenwhich is the $$$lca(a, b)$$$ in the centroid tree and check if $$$dp(a) + dp(b) \leq k$$$. But the condition may be false forcenand true forCP[cen]orCP[ CP[cen] ]and so on.I fixed the test, the first line was missing.
I see. Indeed, it seems that I should have checked extra that $$$dp(a) + dp(b) \leq k$$$ or that $$$dp(a) + closest(cen) \leq k$$$ and $$$dp(b) + closest(cen) \leq k$$$.
Thanks a lot. I was struggling a lot to find the flaw in my reasoning.
EDIT: It seems that even with the extra condition it's not passing test 10, so it wasn't because of that. Any ideas?
New code: https://codeforces.me/contest/1307/submission/71366378
Early today I submitted your code but with a loop thought the $$$CP$$$'s and it TLE'd test 17 71358892.
You can omit vertices 9-15 in a drawing, they just force the centroid to be 4.
Why does my B fail? 71327169.
Answer is min over all ceil(x/itr) if itr>=x or 2 if itr<x for all itr
Why does $$$answer$$$ equal to $$$x$$$ in the beginning? Shouldn't it be $$$inf$$$ or something?
Consider test
$$$1$$$ $$$1$$$
$$$2$$$
Dammit!!
Thanks bud.
Yo Chris,
I really like to see the round authorship! I might not have done so hot (good thing I was on an alt!) but I have a lot to learn from here ;)
It’s cool to see that you and Daniel are authoring problems for both USACO and CodeForces... I wish that I could learn to do the same too. See you in the next contest!
Nathan
Thank you for the positive feedback! We tried our best to make a round everyone would enjoy.
Thanks a lot for this contest.
Another name added to my shit problemsetters list. :)
Hi! I am open to constructive feedback. Which part did you have problems with?
For C, it would probably have made sense to write explicitly what you mean with 'arithmetic progression' (in particular since you were not referring to the usual definition which allows negative differences). That would probably have saved a lot of people some time and WA.
Valid point, but on the other hand, strings with negative index difference cannot be called subsequences, since they're impossible to obtain by crossing out letters in the original string (which is the definition of subsequence).
Hmm that's true, I hadn't thought of that.
Would this be a simpler solution to D?
Use BFS to find the shortest path, now, first sort the shortest path, and for each integer not in the path, check if it is in the special fields — if it is, print the length of the shortest path.
Otherwise we loop over each node in the shortest path until we have found one that is special, once we have found this we loop until we have found the next one. We save the distance, and keep only the minimum distance at the end. we now return the length of the shortest path minus this distance plus one. It essentially corresponds to the two cases "we can place a path that is not on the shortest path"(in which case the shortest path will have the same length) or "We must place the path inbetween two nodes in the shortest path, reducing the length of the shortest path by the distance between those two nodes plus one".
As the graph is not always a tree(can have cycles), there can be multiple paths from 1 to n. Consider this case
Connecting 3 and 5 will not reduce the shortest path
I also did the same, but this approach gives WA. I couldn't understand the reason behind it.
My code : 71327190
Try this testcase
And instead of down-voting, can you guys please point out where is the mistake? I also thought of the same approach but it gave WA. I found a counter-example but are there any more possibilities where this approach could go wrong?
Indeed pretty weird that people are downvoting. Im simply trying to learn where i went wrong
.
Your solution to second problem is O(nlog(n)), not O(n), because you are using set.
As the author said in the code, you don't have to use set. Set is just used to check if some number in it, this could also be done in O(n) easily.
In D, can anyone explain why my solution is wrong?
my solution
My Logic was: 1.normal bfs to get the level of each node.
2.sorting special nodes in order of their distance from node 1.
3.getting the pair of nodes which has the minimum amount of difference w.r.t distance from node 1.
4.connect them then do the bfs again to get the distance from node 1 to node n.
Similar approach, same question :( 71327933
Why do you want to minimize the distance w.r.t. distance from node 1? That makes about as much sense as the number of points you got for your solution. Suppose two special fields already have a road between them, but your algorithm instead will place a road between some other nodes which have minimum difference. Might as well choose two random nodes. At least the probability of correct solution will be uniform.
if one node lets say x is Xi distance from 1 and another node lets say y having Yi distance from 1. Then I want to minimize the difference between (Xi-Yi). Placing another road will have no effect which is independent of the fact you suggested
Suppose two special fields already have a road between them, but your algorithm instead will place a road between some other nodes which have minimum differenceHi! Consider this case:
$$$8$$$ $$$7$$$ $$$3$$$
$$$1$$$ $$$7$$$ $$$8$$$
$$$1$$$ $$$2$$$
$$$2$$$ $$$8$$$
$$$1$$$ $$$3$$$
$$$3$$$ $$$4$$$
$$$4$$$ $$$5$$$
$$$5$$$ $$$6$$$
$$$6$$$ $$$7$$$
Your solution incorrectly connects node $$$1$$$ and $$$8$$$. Optimal solution connects $$$1$$$ and $$$7$$$. Hope this makes sense!
Hi! Thank you for the test case. I had written a similar solution. However, I am still struggling to understand the solution in the editorial. What is the intuition behind sorting on the difference of the distances from source and destination? Could you help?
We assume without loss of generality that $$$x_a+y_b \le y_a+x_b$$$. If you rearrange this inequality, you get $$$x_a-y_a \le x_b-y_b$$$. We see that sorting on the difference $$$x_i-y_i$$$ leads us to the rest of the solution.
Hope this helps.
My understanding of the intuition behind the sorting is to order the fields so that when you iterate through them, $$$min(x_{prev} + y_{cur}, y_{prev} + x_{cur}) = x_{prev} + y_{cur}$$$. In other words, as you iterate, you can achieve the longest distance by taking the biggest $$$x$$$ seen so far and pairing it with the current $$$y$$$.
Really good intuition. Thank you!
Yea exactly, reduces from n^2 to nlogn by gauranteeing that if we take a max yb for a given xa it will indeed be smaller than or equal to xb + ya and we avoid additional checks. Nice Question :)
I don't get it. Can you please explain why would it always be smaller than or equal to xb + ya ?
Coz you sorted according to the constraint
Much appreciated ,but i still don't get it.
The idea is similiar to following. Given array of numbers $$$a$$$, find $$$max$$$ of $$$(\min\limits_{i,j}$$$ $$$(a_i, a_j))$$$.
Naive solution is $$$O(N^2)$$$, where you select both indices. But, alternatively, you can sort the array, and then you know that for some $$$i$$$, taking $$$min$$$ with anything to the right will give $$$a_i$$$, and anything to the left will give that thing. So, now, you only need to go through the sorted list and take best value of adjacent indices.
Basically, for maximizing $$$min(A,B)$$$, we try to keep $$$A$$$ and $$$B$$$ as close as possible. In particular, for the given problem, we need maximum of $$$min(x_a + y_b, x_b + y_a)$$$, so we try to keep $$$x_a + y_b = x_b + y_a $$$, i.e. $$$x_a - y_a = x_b - y_b$$$. This tells you, sorting by $$$x_i - y_i$$$ should give adjacent ones which you should compare and take max over them.
Thank you so much. Your explanation was really helpful.
"So, now, you only need to go through the sorted list and take best value of adjacent indices." why do we have to iterate? Think of sorting them, say in ascending order, isn't the answer N-1th element? Because Nth element is the biggest element all over the array, and N-1th element is the second-biggest element, and when we get min of them it gives second biggest element.
It was an example to give some insight towards the intuition behind sorting. Ofcourse, from the function itself you can see that the second max is the required answer for the example.
Hi Samarth thank's for your explanation can you please simplify a bit more. i not able to understand it completely.
Lets pick out subtask. There are two arrays: $$$x[1..n]$$$, $$$y[1..n]$$$. We need to maximize $$$min(x[i] + y[j], y[i] + x[j])$$$ for all $$$i$$$ != $$$j$$$.
We can simply iterating $$$i$$$ and $$$j$$$ and update ans, but complexity is $$$O(n^2)$$$, not so good. But what happens, if we rearrange pairs $$$x[i],\,y[i]$$$ so that for fixed $$$j$$$ and all $$$i < j$$$:
Lets see the sample:
Let $$$j = 7$$$. As we can see, for all $$$i < 7$$$
Considering this we can simply take the maximum value of all previous $$$x[i]$$$. This value we can take by maintaining $$$max_x$$$ on the preffix.
Ok, but how we can rearrenge elements $$$x[i],\,y[i]$$$ to take $$$ min(x[i] + y[j],\,y[i] + x[j]) = x[i] + y[j] $$$ for all $$$i < j$$$? Simply:
equals to
So, we can sort $$$x[i],\,y[i]$$$ by value $$$(x[i] - y[i])$$$ in not decreasing order.
Total algorithm:
Explanation is turned out toooo long, but I hope it will be understood by everyone :)
Thank you a lot for your explanation, I think I got the idea, but I think there is a little typo over there : "But what happens, if we rearrange pairs x[i],y[i] so that for fixed i and all j>i:" Did you intend to say "for fixed j and all i<j"? Because you gave an example for j=7 and it seems j is fixed there. Or am I missing something?
Yes, it is a typo... I`ll fix it now!
Thanks that helped me. But one question isn't connecting 7 and 8 is also a solution here.
Yes, that works as well.
I found the distance of all the special nodes from node 1 then sorted the special nodes by their distance. Then added an edge between a pair of special nodes, which are closer than other pairs of special nodes. Finally calculated the shortest distance again and printed it. Where my approach gone wrong?71327933 :(
Very Fast Editorial. Thanks FieryPhoenix
I wonder in problem C let s be "aababaabb" and suppose the hidden message is : "aab" what's the number of occurrences of it ?
24 I guess
according to the code of sol, the answer is 15 !!
Sorry, I forgot what the taks is, I counted all the subsequences that equal to given string
Notice that you can't consider all the "aab" subsequences.
"She considers a string t as hidden in string s if t exists as a subsequence of s whose indices form an arithmetic progression"
It has to be in AP as well !
Write solutions in C++ or python please, C is messy and unreadable (especially for D).
Can anyone explain me the editorial of C?
As we are only searching for those sub sequence, which have arithmetic progression, if the size is >2 like if we get a sub-sequence abc 5 times, we will obviously get subsequence ab 5 times,or even more :D . Thats why we are only checking between sub-sequence of size 1 and 2. Now, lets come to the code, there we have two array for memoization. In the first array arr1, we simply count the occurrence of char c upto i. In the second array arr2 ,at arr2[j][c] we add the occurrence of character j, before character c. Which ends up calculating, how many times we got sub-sequence jc upto ith position of the string. Then we find the maximum of occurrence of all those, sub-sequences of length 1 and 2. Which is the answer! :D Well, I know, you have solved this problem, but still wrote this whole just to "memoize" this technique in my memory! :p
On problem B in test case 1,15 is the maximum number and we have to reach at the point 10.So only 1 hop is needed in my opinion.So why max(2,ceil(d/max)) is the solution?
I suppose you haven't completely understood the problem. It is not sufficient to go past the endpoint. On the last hop, you must land exactly at the endpoint. In the given example, just taking one hop can get you to x = 10 but your y would be sqrt(125). Hence, a minimum of two hops would be required. (0,0) -> (5,sqrt(200) -> (10,0). Hope you understood.
1307D — Cow and Fields Can anyone explain the editorial in more detail?
Sure, correct me if i am wrong tho. So basically we need max ( min(xa + yb,xb + ya)) over all a and b. Prev point is obv. Ok now ,
Suppose xa are x1 , x2 , x3 , .. xn and corrosponding yb are yb are y1, y2, y3 , ..... yn Now suppose u start with the first x1 and get max(y2,y3,y4, .. yn) this can be done using a suffix max array and thus u get max with O(1) . Suppose for x1 u get y5 to be max but here comes the most important part u don't know if x1 + y5 <= x5 + y1 or not !!!. So if not u check 2nd to largest number and thus overall complexity would be O(n^2) as u need to consider all cases of y for each x.
So the trick here that is used is sorting on the basis of xi — yi. Now suppose we do what we were doing previously x1 + y5 we choose y5 from suffix max , so we are sure now that x1 + y5 <= x5 + y1 and we can proceed to the next x to get optimal y for it. and after considering all cases we get the max answer which is required. Also suppose the optimal path dosen't include any magic points. So we also check dist[0][n — 1] which is the distance from last point to 1st or vice versa .
Thus we reduce complexity from O(n^2) to O(n logn).
Hope it Helped
How would C change if the subsequences's indices didn't have to be in an arithmetic progression?
Consider this example "aaabbbccc", there would be 27 occurrences of the string "abc". However, if we consider AP, there would only be 3.
I know I was asking if someone has a solution for this
In D solution can be made simpler by following observation. If there are two special fields with distances to $$$1$$$ and $$$n$$$ being $$$(x1, y1)$$$ and $$$(x2, y2)$$$ such that $$$x1 \le x2$$$ and $$$y1 \le y2$$$ then putting an edge between them won't make shortest path shorter. Because of that if we sort them by x they are automatically sorted by y as well :) (but in a different order). Then it makes sense to check only the neighbouring pairs in this order.
wtf I checked the neighboring pairs at first. But I thought it's incorrect and then resubmitted it before the end of the contest.
Can you please tell me how are y automatically sorted if pairs are sorted by x. If I suppose I have distances to 1 and n be (x1 y1), (x2 y2), (x3 y3) be sorted by x. Then if we compare only the adjacent elements we never compare y1 and y3.
How do we know that y2 < y1 and y3 >= y1 won't exist?
Maybe I oversimplified my description, sorry for that. I meant the following:
1) Sort pairs in nondescending order
2) Check if there is any pair of pairs (x1, y1) and (x2, y2) such that x1<=x2 and y1<=y2. That can be done by checking only neighbouring pairs in that sorted order.
2)1) If there is such a pair of pairs you can simply output original distance from 1 to n
2)2) If there isn't you can assume that y values are sorted in descending order
Can you explain a bit more . I don't get how if we sort according to pair and check only neighbors we are assured x1 <= x2 and y1 <= y2. Is it not possible that (x1 <= x2 and y1 >= y2) and (x1 <= x3 and y1 <= y3).
But in your example if we sort by x then x2<=x3 and y2<=y1<=y3, so second and third pair are ones we are looking for. The fact that I use is that if sequence is not sorted in our favourite order there is a pair of neighbouring elements witnessing that.
Gotcha, thanks for the explanation.
Also u only take pairs for which x1 <= x2 and y1 <= y2. Can't there be a case where it's ok to take points for which x1 <= x2 and y1 >= y2.
Again. I distinguish two cases on whether a pair like x1<=x2 and y1<=y2 exists or not. If there is such a pair, I put an edge between corresponding vertices. If there isn't I know sorting by x in ascending order is equivalent to sorting y in descending order and I have a different reasoning for this case which amounts to basically the same thing done again — checking putting an edge between neighbouring vertices cause suffix maximum of ys is always in the beginning of that suffix.
In problem D, can anyone see why picking the two special fields farthest from n would not work?
Consider the case:
$$$6$$$ $$$5$$$ $$$4$$$
$$$1$$$ $$$3$$$ $$$5$$$ $$$6$$$
$$$1$$$ $$$2$$$
$$$2$$$ $$$3$$$
$$$3$$$ $$$4$$$
$$$4$$$ $$$6$$$
$$$6$$$ $$$5$$$
Connecting the farthest fields $$$1$$$ and $$$3$$$ is suboptimal compared to connecting $$$5$$$ and $$$6$$$.
Sorry, I should have specified: except for cases where there's already an edge between any two special fields (in such cases the answer will be "just build the extra bridge between two special fields that are already connected").
If you modify the test case slightly, the same reasoning holds. Connecting the farthest fields $$$1$$$ and $$$3$$$ is suboptimal compared to connecting $$$7$$$ and $$$8$$$.
$$$8$$$ $$$7$$$ $$$4$$$
$$$1$$$ $$$3$$$ $$$7$$$ $$$8$$$
$$$1$$$ $$$2$$$
$$$2$$$ $$$3$$$
$$$3$$$ $$$4$$$
$$$4$$$ $$$5$$$
$$$5$$$ $$$8$$$
$$$8$$$ $$$6$$$
$$$6$$$ $$$7$$$
Thank you!
Problem D: I sorted d1[a] < d1[b] and maximized result by getting sum of the neighboring pairs d1[a[i]] + dn[a[i+1]]. It was accepted. But i think it go wrong if a[i] or a[i+1] is not on the path from 1 to n because dn[] is not decreasing. Was my observation is wrong ?? And does my compare function really work ?? Thank advance ^_^
Thanks for the fast tutorial <3 Thanks for the problems <3 Thanks problem setters <3
Thanks for participating <3
Thanks for answering my questions <3 But sorry for not having done C-problem ;-;
Maybe it was a big deal of fault on me. I failed to notice the possibility of precisely an favorite number of $$$x$$$. so I only counted on the $$$Maximum$$$ and failed on pretest 2.
Can someone explain Problem B more intuitively ?
emm,I think the picture maybe ...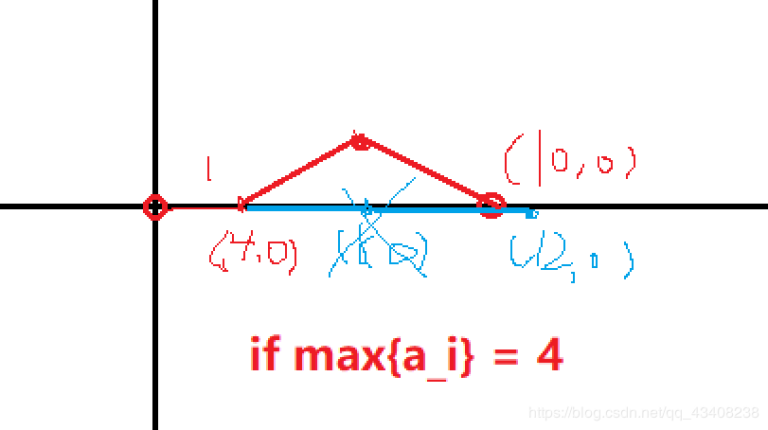
yes, I too couldn't really get the mathematical intuition behind the problem.
Lets name the biggest number in array a ,L.
At first move to right until your dour distance to destination is less than l.
If your not at the destination you just need to make sure that you can move to destination with two moves.
Imagine tor in point y and destination is in point x. Draw a two circle with diameter l. One from the central point x and one from y. You can go to the intersection of these two circles from y and then go to x.
This picture might help.
Is it necessary that he will always use one single number. How about the rabbit moves to right until the destination is less than L(the largest fav. number) but the remaining distance is one of the fav number. He can complete it in 1 single move instead of making 2 moves using the L(the largest fav. number)
Hi! I think that the official solution works in both cases (1st case: we can use multiple times a single [favorite] number; 2nd case: we can use multiple times all [favorite] numbers).
Regarding the situation you described above, look at the following example:
Input:
2 10
3 1
Output:
4
1st case (4 hops): (0, 0) -> (3, 0) -> (6, 0) -> (8, sqrt(5)) -> (10, 0);
2nd case (4 hops): (0, 0) -> (3, 0) -> (6, 0) -> (9, 0) -> (10, 0).
So, the answer is the same in both cases. The main idea is to use the last 2 hops to cover the range [6, 10], not the range [9, 10] as you initially thought.
You can reach up to (5* k) distance to any point using k jumps (chosen favourite number 5)
In problem B , after reaching (d,0) what is the guarantee that the last two hops will cover the remaining distance and it's always will be a favorite number ? Can anyone explain a bit further ?
I got it
In the solution of problem F , does someone could tell me what does
int A2=walk(A,B,K+1),B2=walk(B,A,K+1);mean ? It seems thatA2,B2hasn't been used. Thanks in advance.FieryPhoenixYes, you are right. That line is unnecessary and was from debugging. Edited the code :)
In my code, the output is the next input.
https://codeforces.me/contest/1307/submission/71311150
if you input : 2 4 230023 12 12 2000 12
4 230023 19 43 200 434 1000
you will find the second test is print 531.
I was wrong
help me! B!
https://codeforces.me/contest/1307/submission/71377477
if you input 1 2 4 1 3.
i use the arrays to keep the favorite numbers.but the a[0] sunddenly become 4.
i do not understand why the a[0] is change.
please help me! thanks!
Replace "if (a[i] = x)" with "if (a[i] == x)"
For the problem E Does anyone have another solution to the E problem?
Found an $$$O(n)$$$ solution* for problem E: 266399079
Solution is almost the same as the official one (fix $$$x:=$$$ the rightmost index of a sleeping cow that came from the left side), with an additional observation:
For a fixed sweetness $$$s$$$, the sets $$$L:=\textrm{set}(\textrm{cows with favorite sweetness } s \textrm{ that are allowed to be placed on the left side})$$$ and $$$R:=\textrm{set}(\textrm{cows with favorite sweetness } s \textrm{ that are allowed to be placed on the right side})$$$ must satisfy the property that one is a nonstrict subset of another, so the total number of cows with favorite sweetness $$$s$$$ that are allowed to be placed on both sides is $$$\min(|L_s|,|R_s|)$$$; no need for binary search
(using 0-indexing)
Let $$$I$$$ be the list of indices $$$i$$$ s.t. the $$$i$$$-th unit of grass has sweetness $$$s$$$, in increasing order. Let $$$H$$$ be the set of hunger values of cows that have favorite sweetness $$$s$$$.
Then $$$L=\textrm{set}((s,h) : h\in H \ \land \ I_{h-1}\le x)$$$ and $$$R=\textrm{set}((s,h) : h\in H \ \land \ I_{|I|-h}>x)$$$. Since the booleans $$$I_{h-1}\le x$$$ and $$$I_{|I|-h}>x$$$ are both monotonic w.r.t. $$$h$$$, $$$L$$$ and $$$R$$$ are both of the form $$$H\cap\textrm{set}(0,\dots,V)$$$ for some integer $$$V$$$ (the comments in my submission are slightly incorrect). The result then follows.
*technically my solution is $$$O(n \log(\textrm{MOD}))$$$ and the official solution is $$$O(n \log(n) \log(\textrm{MOD}))$$$
Sorry my solution is wrong.[deleted]
.
Problem D: I sorted d1[a] < d1[b] and maximized result by getting sum of the neighboring pairs d1[a[i]] + dn[a[i+1]]. It was accepted. But i think it go wrong if a[i] or a[i+1] is not on the path from 1 to n because dn[] is not decreasing. Was my observation is wrong ?? And does my compare function really work ?? Can anyone explain to me ?! Thank advance ^_^
In 1307D - Cow and Fields, can someone explain how to maximize min(xa+yb,ya+xb)?
Okay I'll try. Let's iterate over x_a and find some y_b s.t b>a (we can maintain a suffix maximum array and check for b from [a+1,n]), and let's say for all iterations it is the maximum answer. So are we done ? No because we never checked that if x_a + y_b <= x_b + y_a or not. So to check this as well simply means complexity goes to O(n**2).
So what should we do ?
We have two arrays x and y right. Let's sort them according ( x_i — y_i ) in ascending order and let's again follow the above procedure (In mind just think that field number's have been changed). Now again I iterate over x say I am at x_a and every time suing suffix maximum array I select a some value from [a+1,n]. say we get y_b. Using sorting we now don't have to worry than if weather x_b + y_a is smaller than x_a + y_b or not because the former one will always be greater. In short we reduced the some unnecessary computation and still being able to find the actual answer.
Thanks a lot bro, it really helped.
Can anyone tell me where I went wrong.(https://codeforces.me/contest/1307/submission/71392396) I used Dijkstra to find the shortest path, and checked the special fields in the shortest path. If the count of special fields equals k then I take those special fields which are closest, else print the shortest path length in dijkstra.
Why sort in problem D is needed? I cant imagine why is necessary. Can anyone help?
I got it. My main problem was the second inequality (where it comes from). So if we want maximize this inequality (without loss of generality, suppose): xa + yb ≤ ya + xb.
We can now modify this inequality to: xa — xb ≤ ya — yb and now this is prove, sort is helpful (sort do this).
Please explain to me the greedy strategy for D: Now we want to maximize xa+yb subject to xa−ya≤xb−yb. This can be done by sorting by xi−yi and iterating a over x while keeping a suffix maximum array of y to compute maxb>ayb. FieryPhoenix
yes please. I couldn't get how to maximize??
Problem 1307D - Cow and Fields can be solved in linear time 71305246 doing a topological sort over the shortest paths graph.
How does your code work? Can you explain more detailly ? Thanks.
Every edge that don't belong to the shortest paths graph from node $$$1$$$ can be deleted, because it isn't optimal traverse along it before take the added edge, so the graph now is a DAG and have a topological order, in that order the added edge connect two special nodes so for every special node $$$u$$$ if it's a extreme of the new edge is optimal connect $$$u$$$ with the node that maximize the distance from $$$n$$$(in the original graph) and is at the right of $$$u$$$ in the topological order.
We can also use the bucket sort in $$$O(n)$$$ instead of $$$O(n \log n)$$$.
Yeah, But I wanted to share another solution that involve more thinking about graphs and for my it's cool and simple. Btw you are one of my favorite
L$$$\color{red}{\textrm{GM}}$$$.thanks for your code.
I was stuck on the problem for a long time, and through your thought, write a reduced version 71464704
It can use the order of bfs queue instead the topological sort. because for v in g[u] there does not exist a node q such that have an edge (q, v) and d[q] != d[u], so we can ignore the degree of a node.
You can ignore the degree of a node because the bfs order is a topological order of the shortest paths graph, awesome ;)
I have another explanation from bfs order.
let special node a, b satisfy d(a) < d(b) and have an edge, then it can prove d(a) + 1 + dn(b) <= d(b) + 1 + dn(a)
there are 3 cases would be consider:
d(n) < d(a) < d(b)
then the shortest path just consider 1 to n
d(a) < d(n) < d(b)
then the shortest path just consider 1 to n or 1 to a to n
d(a) < d(b) < d(n)
d(a) + 1 < d(b) + 1, |dn(b) — dn(a)| = 1 since they have an edge
note if x ∈ {a, b} s.t. d(x) + dn(x) > d(n), then the shortest path would not walk through x.
Can someone explain problem B more elaborately.
I am not able to understand this part
"This is true because clearly the answer is at least ⌈d/y⌉: if it were less Rabbit can't even reach distance d away from the origin."
consider y = 2, d = 7
then 2 + 2 + 2 + 2 > 7
if less than d would be like
2 + 2 + 2 < 7
2 + 2 < 7
2 < 7
all above can not reach the (d, 0)
the key point is if the last hop exceed (d, 0), it should hop 2 steps with different directions to the target.
my code: 71503153
https://codeforces.me/contest/1307/submission/71438968 Can anyone please tell why my code is giving RUNTIME ERROR on testcase 6 ?
problem D can be solved using a random)
In problem D, I'm getting Wrong answer on Test case 9 if I am using STL map in c++, while on submitting using vector pair and sorting I'm getting Accepted. Can you help why is this happening.
Solution with map : https://codeforces.me/contest/1307/submission/71540983
solution with Vector pair : https://codeforces.me/contest/1307/submission/71540823
map and vector are initialized on Line 71.
the map store only one value for the same key. You may use multimap
Got it thanks, how could I forget about it. Anyways Thanks
Why down voting? I just wanted to help
I'm gonna explain other approach for D cows and field, it is somewhat similar as explained in tutorial but is easier to understand first of all find distance of each node from source and destination which can be easily done by bfs . now sort all the special nodes with respect to their distance from destination now consider two special nodes 'a' and 'b' , dist of 'a' from source is x, dist of 'b' from destination is y and dist between 'a' and 'b' is z (z>1) and as of now shortest path was x+z+y but if we connect 'a' and 'b' the shortest path becomes x+y+1 which is lesser than the previous one as soon as we connect two special nodes some intermediate nodes are skipped and shortest path is decreased. we want to minimize the skipped nodes such that decrease in shortest path is minimum. now the special nodes are sorted with respect to their distance from destination Traverse the special nodes and try connecting each special node with next special node and calculate shortest path after each connection and return maximum answer here is my solution https://codeforces.me/contest/1307/submission/71542301
can anyone explain in problem B why are we doing ceil(x/far) for x>=far?? Thanks in advance:)
lets assume x = total distance to cover and far = max jump size if x == far then the ans is 1 straight away. In this question a greedy approach is, we can just do all the jumps horizontally with max jumps size, if x is divisible by max jump size then ans will be just (x/far) no need of ceil function but if x is not divisible by far then a small distance will be left at the end, so to handle that last two jumps will not be horizontal they will make a triangle like this due to which we will have to use ceil function
this image will help you understand better https://postimg.cc/ctMvVrCg
I can't understand this part of code in your solution for problem F.
Should't it look like these?
To make the implementation easier, we split every edge into two (as described in the editorial). Therefore, two nodes can reach each other directly if their distance $$$\le$$$ $$$2K$$$.
Why splitting each edge into two with an additional node makes the implementation easier?
ok, I am kinda get it.
Basically the idea is rest stop groups expand their reach radius by k/2, and non rest stop cities make are trying to walk distance of k/2 to reach any rest stop groups.
But when k is odd, it's complicated to divide the breaking point.
Am I right?
Well, the complicated case is when the distance between two nodes is odd, because there is no easy breaking point for our parallel BFS. Splitting edges into two guarantee that all pairwise distances between nodes are even.
Thanks
If someone failing in D, he/she can try this case too.
13 12 2 1 9 1 2 2 3 3 4 4 5 1 6 6 7 7 8 8 9 1 10 10 11 11 12 12 13
What is the intuition in sorting
x_i - y_i? I needed to sort the special vertices in such a way that in any shortest path involving two special vertices x and y, x comes before y in the shortest path. I did sorting by {-y_i, x_i} because I want to get farthest fromnfirst, then tie break by closest to1. I got AC for this.This is deleted
Editorial for problem C turns out to be wrong.
for case aabbcc
it gives answer 4 but answer is supposed to be 8
abc (1,3,5) (1,3,6) (1,4,5) (1,4,6) (2,3,5) (2,3,6) (2,4,5) (2,4,6)
correct me if i am wrong
indices are not in AP (1,3,6) (1,4,5).....
Nice Editorial and wonderful problems
editorial is not working for me, is there any way to fix
For those who dont really understand 1307D - Cow and Fields, here's my code that might help u. I have put some personal notes in there: 214379142
For question C https://codeforces.me/problemset/problem/1307/C In test case lolollll lol will be 8 and lo will be at max 3 times. So here the explaination provided for question C proves wrong can anyone pls verify.
Can someone tell me where does my solution fail in problem D ,
I try to do the following :
$$$d1(a)+dn(b)+1$$$ $$$\leq$$$ $$$d1(n)$$$ , where $$$a$$$ and $$$b$$$ are special vertices ;
Then for each $$$a$$$ , I find the max corresponding $$$dn(b)$$$ (if exists) that satisfies the upper condition , using binary search on $$$dn$$$ .
Then take the maximum over set of $$$d1(a)+1+dn(b)$$$ , if the set is empty then the output if $$$d1(n)$$$ , otherwise the maximum
275393405
For the Problem D , Cows and Fields , How do I ensure :
Remember that an upper bound of the answer is the distance between field 1 and n