Алиса живет на плоской земле, которая может быть представлена как квадратная решетка $$$n \times n$$$ со строками и столбцами, пронумерованными от $$$1$$$ до $$$n$$$. Обозначим клетку на пересечении строки $$$r$$$ и столбца $$$c$$$ упорядоченной парой $$$(r, c)$$$. Каждая клетка решетки является либо землей, либо водой.
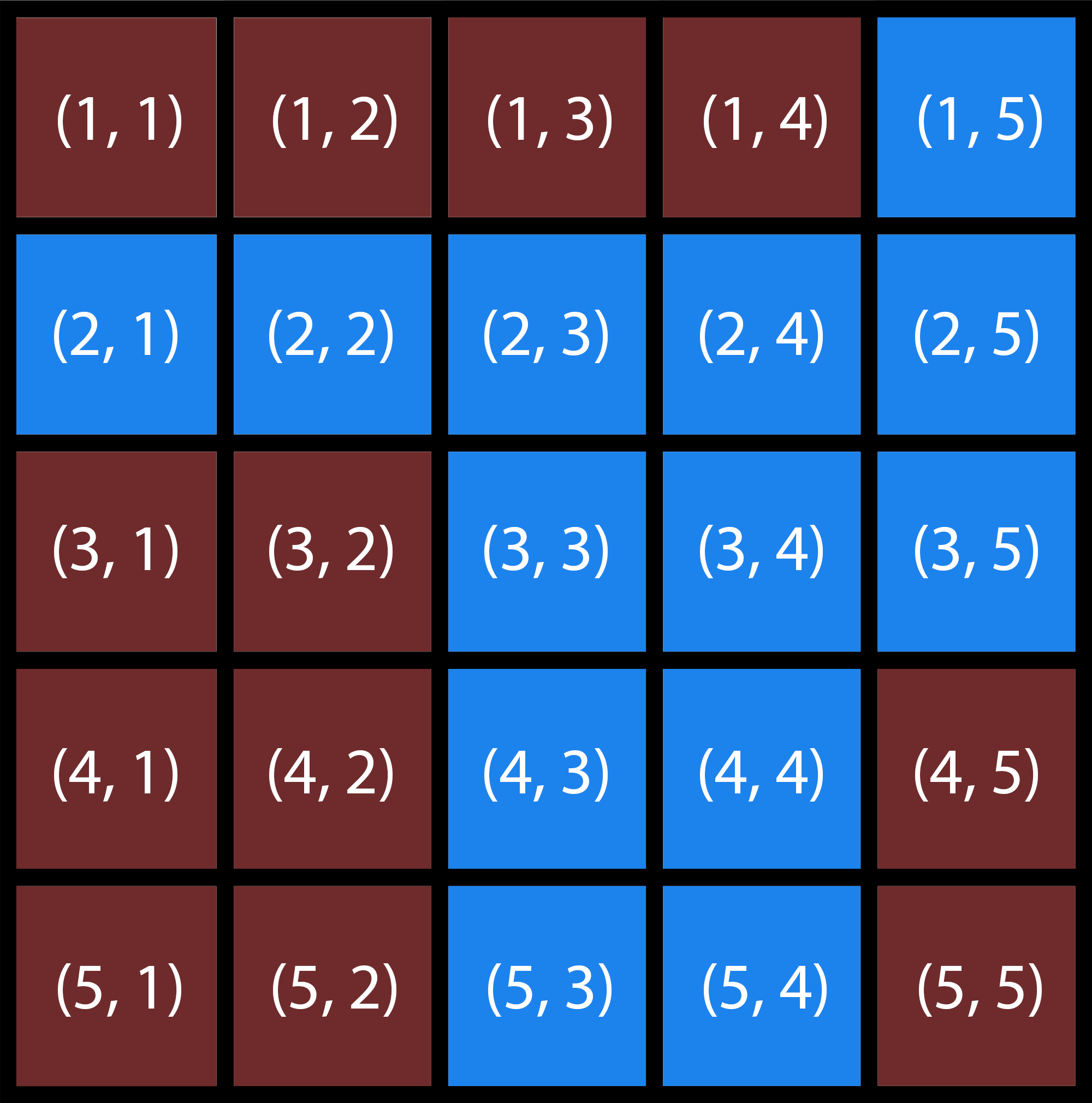 Пример планеты с $$$n = 5$$$. Она также является первым примером.
Пример планеты с $$$n = 5$$$. Она также является первым примером. Алиса живет на клетке, которая является землей, $$$(r_1, c_1)$$$. Она хочет добраться до другой клетки, которая является землей, $$$(r_2, c_2)$$$. В любой момент она может переместиться в одну из соседних с ней ячеек — в одном из четырех направлений (т.е. вверх, вниз, влево или вправо).
К сожалению, Алиса не умеет плавать, и можно перемещаться только пешком (т.е. только по земле). В итоге путешествие Алисы может быть невозможно.
Чтобы помочь Алисе, вы хотите создать не более одного туннеля между какими-то двумя земляными клетками. Туннель позволяет Алисе перемещаться между двумя его концами. Создание туннеля требует некоторых затрат: стоимость туннеля между клетками $$$(r_s, c_s)$$$ и $$$(r_t, c_t)$$$ равна $$$(r_s-r_t)^2 + (c_s-c_t)^2$$$.
Таким образом, ваша задача — найти минимальную стоимость постройки не более одного туннеля так, чтобы Алиса смогла добраться от клетки $$$(r_1, c_1)$$$ до клетки $$$(r_2, c_2)$$$. Если постройка туннеля не обязательна, стоимость полагается равной $$$0$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 50$$$) — длину стороны квадратной решетки.
Вторая строка содержит два целых числа, разделенных пробелами, $$$r_1$$$ и $$$c_1$$$ ($$$1 \leq r_1, c_1 \leq n$$$), обозначающих клетку, где находится Алиса.
Третья строка строка содержит два целых числа, разделенных пробелами, $$$r_2$$$ и $$$c_2$$$ ($$$1 \leq r_2, c_2 \leq n$$$), обозначающих клетку, куда намерена попасть Алиса.
Каждая из следующих $$$n$$$ строк содержит строку из $$$n$$$ символов. $$$j$$$-й символ $$$i$$$-й такой строки ($$$1 \leq i, j \leq n$$$) это 0, если клетка $$$(i, j)$$$ — земля, и 1, если клетка $$$(i, j)$$$ — вода.
Гарантируется, что и $$$(r_1, c_1)$$$, и $$$(r_2, c_2)$$$ это земля.
Выведите одно целое число — минимальную возможную стоимость постройки не более одного туннеля так, чтобы Алиса смогла добраться от клетки $$$(r_1, c_1)$$$ до клетки $$$(r_2, c_2)$$$.
5 1 1 5 5 00001 11111 00111 00110 00110
10
3 1 3 3 1 010 101 010
8
В первом примере должен быть построен туннель между клетками $$$(1, 4)$$$ и $$$(4, 5)$$$. Стоимость такого туннеля равна $$$(1-4)^2 + (4-5)^2 = 10$$$, что является оптимальным. Таким образом, Алиса сможет дойти от $$$(1, 1)$$$ до $$$(1, 4)$$$, использовать туннель от $$$(1, 4)$$$ до $$$(4, 5)$$$, а затем дойти от $$$(4, 5)$$$ до $$$(5, 5)$$$.
Во втором примере должен быть построен туннель между клетками $$$(1, 3)$$$ и $$$(3, 1)$$$. Стоимость такой постройки равна $$$(1-3)^2 + (3-1)^2 = 8$$$.
| Название |
|---|




