Thanks for participating; we hope you enjoyed the tasks! Look at the bottom of this post for some more challenges.
Feel free to ask in the comment if you have any question. If you have a different solution from ours, share it too. :D
Our approaches
Div2A
Div2B
Div2C
Div1A / Div2D
Div1B / Div2E
Div1C
Div1D
Div1E
Challenges
Div2C
Div1A / Div2D
Div1C



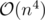 ?
?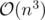 solution, but you could also use a Voronoi diagram for an
solution, but you could also use a Voronoi diagram for an 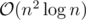 runtime too!
runtime too!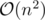 approach to solve the task in linear time!
approach to solve the task in linear time!






The contest was awesome! Thank you.
Wow fast tutorial Thanks for your effort :)
why does the answer is 1 or -1 or 0 for Div2A while I was trying to print the value like it was given in the example test cases, 4 for example test case one and 0 for the second?
If a positive integer works, you can use any positive integer (within the bounds indeed). I'm saying that 1 is one possible answer. You can print 2 or 4 if you want!
why ans can't be 2 for positives,-2 for negative number if more and 0? doubt for -2. please help
It can. It can be anything till it has right sign.
It wasn't accepting. should I share my code with you if you could check once ?
The problem with your code is where you do ceil(n/2) because n/2 is an integer divison. When n = 5, ceil(n/2) = 2 because 5/2 = 2 in integer divison and ceil(2) = 2. Instead you want ceil(5/2) = 3. So either do ceil((double)n/2) or ceil((n+1)/2) so you get the correct value to compare to.
how does the time complexity in div2 C is n^4?
There are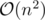 cells, so there are
cells, so there are 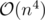 pairs of cells.
pairs of cells.
Really interesting, how many people solved problem E without using google?
Google what exactly?
It is really old problem and it is in google
Do you mean Div1E or Div2E?
I find neither of them on Google.
:(
Solution of Div2E is there
Er... sure...
Where is it? Can you share a link?
Your text to link here... Solution of Div2E is there!
is it funny -.-
I am curious about the Div1C Challenge part. How's that possible?
The challenge is finding the interesting values of g(l, r) without exploring all the states. Think about how you can do that efficiently. I'll post my full approach later!
https://codeforces.me/blog/entry/65520?#comment-495374
Just wondering if anyone has a solution to div1 D that runs asymptotically faster than NsqrtN.
Div1C also can be solved by using SAM.
But I still can't figure out how to solve it when m ≤ 105.
What does SAM stand for? Suffix array m______?
Anyway, see https://codeforces.me/blog/entry/65520?#comment-495120 for now.
Suffix Automaton.
What is 'SAM'?
Suffix Automaton. It can save all substrings of a string.
Let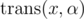 , where x is an SAM node and α is a Latin letter, denote the position we will get to when we transfer x on the edge with every bit of the Morse code of α successively. We'll get a DAG G = (V, E), where V is the node set of the SAM and
, where x is an SAM node and α is a Latin letter, denote the position we will get to when we transfer x on the edge with every bit of the Morse code of α successively. We'll get a DAG G = (V, E), where V is the node set of the SAM and 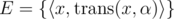 . Therefore, the answer is the number of routes that starts with the root of the SAM, and ends up in another node.
. Therefore, the answer is the number of routes that starts with the root of the SAM, and ends up in another node.
Let f(x) denote the number of routes that ends up at node x. We'll solve the problem offline, so that the SAM of the whole 01-string has been built. Define a sub-SAM of a prefix of S is a subgraph of the SAM and it accepts exactly all of its substring. When we append S[i] to the sub-SAM of a prefix of length i (i.e. S[: i] in Python), the sub-SAM enlarges, and the new nodes has no edge out. So, we can run a DP to get f(x).
Time Complexity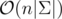 .
.
https://codeforces.me/blog/entry/65520?#comment-495374
An O(n) solution for Div1A/Div2D.
https://codeforces.me/contest/1129/submission/50470292
We can use the structure max-queue, which supports standard push back and pop front, and additionally tells the maximal value in the queue, in O(1).
So we first push each dist(0,j) + n * (out(j)-1) * n + dist(j, e), for each 0 <= j < n.
Then for each 0 <= i < n, in order to take the next station as the beginning, pop the frontmost value (let it be x) and push (x + n), and we consider each value in the queue is decreased by exactly 1. This means that the station we left is delayed by a circle, while the following stations are approaching by 1.
May I ask why the Div2B Greedy solution works? Namely, min(|xi−xi+1|+|yi−yi+1|,|xi−yi+1|+|yi−xi+1|) for each step, leads to the global minimum?
Anyone can helps?
Really appreciate it!
Also curious about this, I strictly used |xi-xi+1| + |yi-yi+1| and that worked.
@gtatutors-ca too:
If we assume xi < yi for each 1 ≤ i ≤ n, then that will work perfectly!
There are actually only six cases to consider:
In cases 1 and 6, it doesn't really matter who goes to where. The distance travelled will be the same.
In cases 2, 3, 4, and 5, you can see that xi should go to xi + 1 and yi should go to yi + 1 for optimality.
Does this address your question?
This makes sense, I didn't think about all these cases. I automatically assumed case 2.
It's fine we only need it to work lol
By "If we assume xi < yi for each 1 ≤ i ≤ n, then that will work perfectly!" Did you mean xi < x_(i+1)? Cause otherwise there will be much more cases other than 6.
Also, I can follow your idea by assuming xi<x_(i+1). But why can we make this assumption?
Now I understand clearly, the greedy approach get the right answer!
Many thanks!
Oh sorry I messed up while listing the cases. Now the post is fixed. I meant xi < yi, and as you said, we cannot assume xi < xi + 1.
still dont get u its the proof for only 1 step
We can consider each step independently, because no matter what our decision is (about who goes where), we will have the same problem to solve.
If may help to realize that it doesn't matter who stays where during each step. We only need a bigger picture of where THEY are (but not where each of them individually is), and that is determined for every step at the very beginning regardless of our decision.
Even more interesting: why even Greedier solution works?
Logic: For every pair of i-th tier shops, Sasha takes a walk to leftmost(smaller index) and Dima to rightmost(bigger index).
See https://codeforces.me/blog/entry/65520?#comment-495118!
Let's say from xi to xi+1 is a round, because either player 1 or player 2 arrived at xi+1 or yi+1 as mentioned in the tutorial, it doesn't matter how they get the next round. So in each round, we can get the minimum answer, and totally in every rounds will be the optimal answer.
For Div1B,we let n=2000 and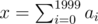 , and a0, a1, ..., a1997 = 0,a1998 = - d,then a1999 = x + d.
, and a0, a1, ..., a1997 = 0,a1998 = - d,then a1999 = x + d.
And then the correct answer is 2000x,and Alice's answer is x + d ,the difference is 2000x - (x + d) = k,so 1999x=k+d,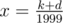 ,so we can let d = 1999 - k%1999 to make x a integer.
,so we can let d = 1999 - k%1999 to make x a integer.
Because k ≤ 109,x is about 5 * 105
Nice! Interestingly people's approaches to this task are very varied.
%%%
that's a good idea!
when I thought about this problem I ended up with some equations and a lot of variables but what I can see from your solution and the solution in tutorials that you assumed values for the variables then you proved that they always will produce the right result
my question is : how did you thought about this problem do you assume the values first then try to prove them or you have some logic that force you to assume these values then you confuse your self by probing them mathematically !!?
values like : (-1 for a0 in the tutorials ),(your 0's in the beginning of the sequence)
Thanks in advance.
At first,I made some mistakes about the problem,I mistakenly think that Alice's answer is k and get a WA,and then I fixed the mistakes and get this method.
sorry, but you seem to not understand me well I just ask you about the intuition behind solving such problems , the way you thought about it to get the solution
I'm sorry for my poor English.
Well,there are three variables,n,x,and d.And We can find that x will be smaller when n is bigger.Because n ≤ 2000,so we want to make x smallest,so I let n=2000,and find a smallest d.And it conforms to the problem.
Am I the only one who in Div1B handled k ≤ 106 with outputting
1
- k
?=)
It was an intended loophole xD
I also did this.
About Div1D, I don't understand the part of 'The Real Thing'.Is it a complexity proof? (Well we can just update f(l,r) using bruteforce according to some accepted codes)
Anyone can help?Thanks!
The tutorial is now updated with a more detailed explanation. Check it out!
for div2-D challenge, I am thinking about any data structure which supports us to push element in back, pop element in back and gives me the max value. if there any data structure, i think i can construct O(n).(as we can write dist(s, i) as a function of dist(0, i)).
for div2/d "that the only thing that matters is the last candy to be delivered." what do you mean by last candy for a source...is it the one which take max time to deliver to destination for a particular source
Least time to deliver for a particular source. The one that takes the most time should be delivered before. Do you see why?
Really sad that I didn't recognize that the error in my solution to Div2B was a simple overflow until after the contest ended.
how the number of over-counted sequences are calculated in 1129C - Азбука Морзе using LCP ? can someone explain ?
The number of over-counted sequences can be calculated by considering the suffix array of T. Namely, for each two adjacent suffixes in the list, we over-counted them by g(l,r) with l and r denoting the corresponding indices of their longest common prefix (LCP).The number of over-counted sequences is the sum of g(l, r) with l and r defined as in the above.
Thanks, but you just copied and pasted what written in editorial. Actually, I have never solved Count distinct Substrings problem using Suffix Array, but I figured out using google.
O(n) solution for Div1A/Div2D : codeforces.com/contest/1129/submission/50443015
Let's define x[i]=n∗(out(i)−1)+dist(i,e) , where dist(a,b) and out(i) represents the same thing as in the editorial and s the current node. now, if we look for every i what is dist(s,i) we will obtain something like this:
suppose n=4;
i=1 : 0 1 2 3 | i=2 : 3 0 1 2 | i=3 : 2 3 0 1 | i=4 : 1 2 3 0 |
so, for i=1, the answer will be max(x[1]+0,x[2]+1,x[3]+2,x[4]+3) and when we move to i=2, all values decrease by 1 except for the first value, which increases by 3 => the new maximum will be either the previous maximum-1 or x[i-1]+n-1. When we get to i=3, again, the maximum will be either the previous one or x[2]+3. So we only need to check the maximum once and then we will know which is the new one in O(1) for every position.
*previous maximum-1 or x[i-1]+n-1, I believe.
yes, thanks
we can use max queue too for O(1).
Can someone explain the answer to Div2D, test case 6, when the starting station is 40? As far as I can understand, the only stations that we need to consider are 3 and 49, because they are the ones that need 2 rounds, since they have 2 candies. Therefore, for 3, we can choose the last candy to deliver to be 31, which is the one that is closest. Therefore, we would need 50 * (2 - 1) + (31 - 3) + (3 - 40) + 50. I add the 50 at the end, so that the distance between the starting station (40) and the station with the candy (3) is positive. In this case, the distance would be (50 + 3 - 40) = 13. This would result in a total of 91, and not 93. When we do the same operations for the second station (49), we result in an even smaller number: 50 * (2 - 1) + (50 - 49) + (49 - 40) = 78. Therefore, the answer would be 91, which is the max(91, 78. Where am I wrong?
actually it is 39 33 that makes the situation worse...
Oh so it's not enough to only take the stations with the maximum number of candies. I can now see why. Thank you.
I tried to solve DIV1C in online fashion. Approach: For every new input say ci (c='0' or '1') I have to add the possible number of english alphabet strings for all suffix strings that are not included yet. I used dp for computing possible number of english alphabets from i= j to 0. I used set with hashing to check if a string is included or not. The complexity of the solution is however same as in tutorial (O(m^2log(m))). But my solution is giving TLE. If someone finds something wrong, correct me please.
I'm not sure if the problem would be the same in c++, but I tried the same solution in java, and hashing was too slow, so I had to use an array-based TRIE.
But that trie reduced ur complexity from O(m*m*log(m)) to O(m*m), isn't it?.... I'm curious how editorialist solution passed... Can you please share it...editorialist-sama :p
I coded it the same way as you. Time complexity is O(m^2 (log(m)+k)) like the tutorial but I'm getting TLE as well. My solution: https://codeforces.me/contest/1129/submission/51106694
Edit: I can get it to pass using 1403 ms if I use unordered_set instead of set. (I had to call unordered_set's reserve() and max_load_factor() functions to speed up the runtime: See https://codeforces.me/blog/entry/21853). The new code which passes in time: https://codeforces.me/contest/1129/submission/51107201.
anybody help me with div2D i didn't understand the tutorial
Can you point out where specifically you got lost in the editorial?
ok. name source s, considering station i and destination d. let's assume, source station is 1. let's consider the station i = 5. then, let's take out(5) = 10 that means that 10 deliveries should be given from station 5. now, to give 10 deliveries, you have to cycle through station 5 for 9 times.(you know why, commonsense). and, you have to go to station 1 to station 5. then, after 9 cycle, you have to go to another cell(to delivery from 5 that's dist(5, d)).
now, go to the greedy approach, we can't minimize the 9 cycles. what we can minimize is the distance between i = 5 and d(taking the minimum distance from i = 5 to any destination). now, is this the answer??? .... nope...
you may got mistake on some area. you have to consider all cells not any particular cells. what we did is the minimum from s = 1 for a particular cell(i = 5). we have to do this for all.
when we are done doing that, we have to take maximum.why??
let's say result for s = 1 and i = 5 is 19 and result for s = 1 and i = 8 is 29. what that means?
from s = 1, delivering all things from i = 5 costs 19, and delivering all things from i = 7 costs 29. what would we take, if we take 29, in the 19th step, we would deliver all things taken from i = 5. if we take 19, we would not consider the case of i = 7.
So, we would take the maximum.
and, that last thing wasn't mentioned in the editorial(to think on your own).
if you need, you can see my code 50476745
thank you so much @zarif_2002
welcome bro.
I hate the way tutorials say something like "and having this we can compute that" without further explanation. The solution is not obvious for everyone. Like I really don't get what happenned in "The Real Thing" part in Div1D.
Now it's updated. Let me know if anything is still unclear.
Problem E contains an interesting subproblem. When determining the direct children of a vertex, we are trying to discover a hidden array of booleans. To do so, we are able to query for the sum of any subset of the array's elements. The suggested approach in the editorial works within the constraints of the original problem, but is not the optimal strategy w.r.t minimizing worst-case number of queries. Is anyone familiar with literature treating this problem?
I’d be interested to know too! Do you have a better strategy? I can only think of D&C which will probably give roughly the same number of queries in the worst case (but probably much better on average).
How do you solve 2c in o(n^3)? Im assuming dsu but not sure how?
For each cell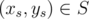 , instead of iterating through all cells
, instead of iterating through all cells 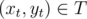 , we should try to only iterate through each possible xt and check, for this fixed xt, what is a yt that minimizes (ys - yt)2.
, we should try to only iterate through each possible xt and check, for this fixed xt, what is a yt that minimizes (ys - yt)2.
To do this, we should pre-process, for each cell (x, y) (not only those in S, but all cells in the grid), a y' that minimizes (y - y')2 such that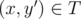 . We can do this by naively iterating through y' for every cell.
. We can do this by naively iterating through y' for every cell.
Each part will run in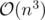 !.
!.
About Be Positive Is it entirely necessary to select 1 or -1 for answers — I thought it did mentioned that its ok if division result is having fraction like 2.5 etc and selecting any number should satisfy as long as result is a positive number for positive and negative number for negative. Besides an example did mentioned 4 as the answer. Sorry if i am missing something .
It's not necessary to choose 1 or - 1. If 1 is ok, 4 is ok too. Likewise, if - 1 is ok, - 27 is ok too.
Assume for now that we are to find, for each suffix of S (not prefix as in the original task), the number of English sequences that translate into some substring of it ("it" refers to "suffix").
Definition. Let g(l, r) be the number of English sequences that correspond to some prefix of S[l..r].
For some fixed suffix S[x..m], consider its suffix array. We can calculate the final answer for it as follows.
Suppose the i-th suffix in the suffix array corresponds to the substring S[Li, m].
Definition. Let li be the length of LCP of the (i - 1)-th suffix and the i-th suffix (if i = 1, li = 0).
The answer for suffix S[x..M] being considered is then: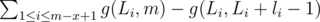 .
.
Key 1. The suffix array of S[x..m] is different from that of S[(x + 1)..m] at exactly one index. Because of this, we can maintain and update our suffix array efficiently.
Key 2. We can calculate g(l, r) in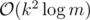 per query using a segment tree (where k = 4 is the maximum length of each code), in which each node stores the corresponding coefficients.
per query using a segment tree (where k = 4 is the maximum length of each code), in which each node stores the corresponding coefficients.
In the original task, we aimed to find the answer for each prefix, not each suffix. To get back to it, we can simply reverse all Morse codes as well as our string S. Let the reversed S be T. Then, the answer for the prefix S[1..x] is the answer for the suffix T[(m - x + 1)..m] (with Morse codes reversed).
More on using a segment tree to calculate g(l, r).
Let us introduce two other functions v and f to formulate g.
Definition. Let v(l, r) be 1 if S[l..r] corresponds to some single English alphabet, or 0 otherwise. (Hence, if r - l + 1 > k = 4, then v(l, r) = 0 for sure.)
Definition. Let f(l, r) be the number of English sequences that correspond to exactly S[l..r].
Therefore,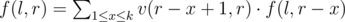 .
.
Then, it follows that: g(l, r) = g(l, r - 1) + f(l, r).
Suppose we want to find f(l, r) (not g(l, r) yet) efficiently using a segment tree. Consider a node that is responsible for S[L..R]. In calculating f(l, R) where 1 ≤ l < L, we can write f(l, R) as a * f(l, L - 4) + b * f(l, L - 3) + c * f(l, L - 2) + d * f(l, L - 1), where a, b, c, d are constants for this particular node (notice that these constants are the same regardless of l). The same is for calculating f(l, R - 3), f(l, R - 2), f(l, R - 1) (but with different constants). The values f(l, R - 3), f(l, R - 2), f(l, R - 1), f(l, R) can then be used to merge with subsequent nodes in the future, for a query f(l, r) where R < r ≤ m.
We can extend this to work with calculating g(l, r) similarly.
This solution runs in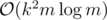 (excluding suffix array construction, the efficiency of which will depend on our implementation).
(excluding suffix array construction, the efficiency of which will depend on our implementation).
Why in Div2C we consider going from source set S to destination set T directly without going to any other intermediate set of cells.
because you can only build a single bridge.
The question says — "To help Alice, you plan to create at most one tunnel between some two land cells." how can one be sure of building only one bridge? why can't we build a bridge between set A and set B, and then between set B and set C, if A is the source and C is destination and B has more than 1 land cell.
The thing is: if you need to construct a bridge from set A to set B, and then another bridge from set B and set C, you are in fact building two bridges, which is not a possible solution.
Also, keep in mind that you can build a bridge from ANY land to ANY land, so even a bridge from point <0, 0> to <50, 50> is still a thing.
In problem D it is not necessary to store q(i) for i < 0. f(x, R) is defined to be the number of elements which appear exactly once in the segment f[x...R]. By definition, f cannot be negative. Hence q(i) = 0 for any i < 0. It is sufficient to store q(i) for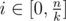 .
.
Your definition of what is stored in each block is different than ours (according to your code). Note that R is the right endpoint of the block, which is different from r.
How to solve d2c in o(n3) ????
so hard :D I have some idea to solve O((8*n)^2), but not sure that its work
What's your approach???
Check https://codeforces.me/blog/entry/65520?#comment-495379!
Thanks man
I think my solution for Div1C is m^2, can someone check it? https://codeforces.me/contest/1129/submission/50547727
Is there a correct algorithm for the first paragraph of Div2/E faster than O(n ^ 2)?
Another O(n) solution for Div1A/Div2D. 50724905
Consider some station i. The front array to store maximum steps when ending with station (1~i-1). The back array to store maximum steps when ending with station (i~n).
I was surprisingly able to solve Div1E using only questions of the following type, despite the seemingly significant loss of information:
Given a set S of vertices and another vertex v, is v on the path between two vertices of S?
My approach was to root the tree at 1, find all the leaves, then add the other vertices to the tree in random order. To add a vertex x, first sort all the vertices already in the tree by depth and then binary search to find a shallowest vertex y that is in the subtree of x (which must exist because all the leaves are already in the tree). Let z be its parent. Add x as a child of z and for every other child of z, check if it needs to be reparented to x. This can be done efficiently with divide and conquer.
It can be shown that this uses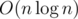 queries (expected).
queries (expected).
Code: 50803526
how can one solve Div2C in O(n^3)?