Привет, Codeforces!

Скоро начнётся XXII Открытая Всесибирская олимпиада им. И. В. Поттосина — соревнование по программированию, в котором принимают участие студенты вузов со всей России, а также стран СНГ. Основной язык олимпиады, на котором написаны условия задач и происходит общение с жюри, — русский.

Олимпиада состоит из отборочного и финального этапов. Отборочный этап (известный также как "интернет-тур") проходит через интернет, и участвовать в нём могут все желающие команды. В этом году по-прежнему финальный этап будет проходить в режиме онлайн, участникам не придётся ехать в Новосибирск. При отборе команд в финал для команд от Сибири и Дальнего Востока выделяется квота не менее 50% от общего числа финалистов.

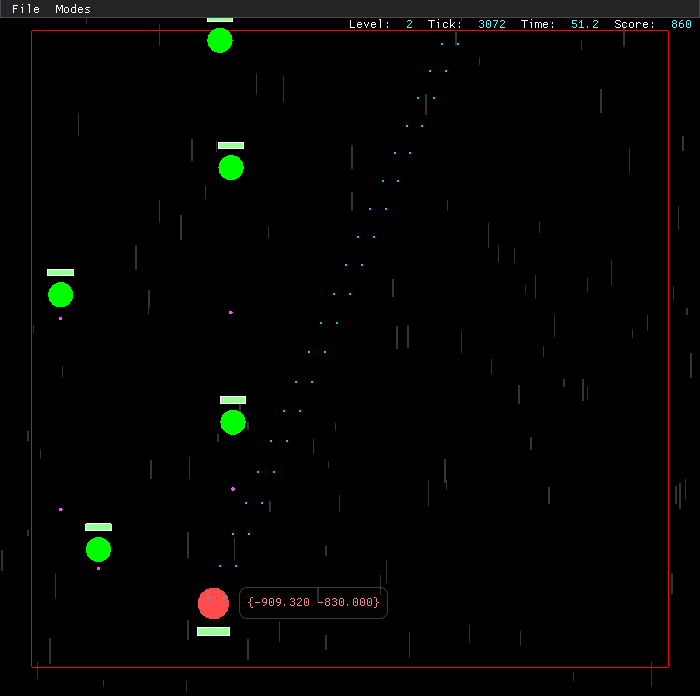
Финальный этап традиционно состоит из двух туров. Один из них проходит по правилам ICPC-олимпиад: 8-12 задач, на решение которых отводится 5 часов. На другом туре участникам предлагается решать одну "большую" задачу в течение 5 часов. Пример такой задачи с прошлого года можно увидеть здесь. Более подробно правила и положение олимпиады можно прочитать здесь.

Отборочный тур состоится в воскресенье, 10 октября, в 10:00 по московскому времени. Очный тур пройдёт с 5 ноября по 8 ноября.

Регистрация в системе тестирования открыта здесь. После регистрации можно порешать пробный тур.

Мир спортивного программирования всё ещё лихорадит от коронавирусных ограничений — шутка ли, привычное время проведения интернет-тура в этом году оказалось занято финалом ICPC позапрошлого сезона! Так что мы решили поддержать общую неразбериху и в качестве эксперимента изменили формат отборочного тура. Кроме того, мы против общей тенденции по использованию трёх компьютеров.

Согласно правилам олимпиады, каждая команда может использовать только один компьютер. Разрешается использовать дополнительные компьютеры только для связи с сокомандниками и для чтения условий задач.

В любой момент времени может быть только один активный компьютер, на котором вы можете писать, компилировать, запускать программы. Активный компьютер может переключаться во время тура, например чтобы следующую задачу писал другой член команды. Однако нельзя проявлять активность больше чем на одном компьютере одновременно.

Использовать интернет разрешается.

Использовать предварительно написанный код разрешается.

В этом году отборочный тур будет длиться 5 часов, но в туре будут задачи разного формата:

• Первые 6 задач обычного формата ICPC. Если решение полностью правильное, то задача засчитывается, и в рейтинг идёт одна зачётная единица.
• Последние 2 задачи оптимизационные. В каждой из них есть несколько уровней сложности, за преодоление каждого уровня даётся какое-то количество зачётных единиц.

Штрафное время по оптимизационным задачам начисляется отдельно за каждый уровень за максимальный решённый уровень — по первой посылке, которая преодолела соответствующий барьер.

Количество зачётных единиц по задачам:

Проведение первой номинации Всесибирской олимпиады в дистанционной форме — дело сомнительное.

Обычно на таком туре выдаётся архив с материалами, в котором лежат собранные исполняемые файлы игры, чекеров, визуализаторов и т.д., и никакие исходники не выдаются. Разумеется, все программы собираются только под винду, и обязательно проверяются на компьютерах участников.

В игровых задачах часто используется межпроцессное взаимодействие, которое нужно полностью переписать, чтобы собрать и запустить игру нативно под другой ОС. Да и система сборки в игровых задачах бывает непростой: например, в 2019 году для сборки нужен был CMake, Conan и опционально Java/Python SDK — сколько участников смогли бы собрать это самостоятельно?

При дистанционном формате каждый участник сидит за своим компом с произвольной ОС, неопределёнными версиями компиляторов и непонятно как настроенными путями. Если работоспособность под виндой и под линуксом мы проверили заранее, то на вопрос о сборке под мак пришлось отвечать вслепую.

Тем не менее, первая номинация в этом году всё-таки состоялась. Участникам предлагалось решать задачу дискретной оптимизации, предложенную компанией Huawei. Задача укладывается в обычный "марафонский" формат: прочитали input из файла, вывели output в файл, дальше проверяется ответ и вычисляются баллы. Это конечно не так интересно, как игра, зато так удалось избежать большинства технических проблем.

Архив материалов можно скачать ЗДЕСЬ. В нём есть условие задачи, в котором описано остальное содержимое. Кроме того, в этот архив включено лучшее решение жюри, так что топовым участникам есть над чем поглумиться =)

Примерное условие задачи: есть клеточное поле M на N, заполненное ящиками, и на нём P порталов в "другой мир". Нужно как можно быстрее вынести все ящики в другой мир, используя K роботов. Роботы бегают как обычно, могут пользоваться порталами и носить ящики. Сталкиваться запрещено.

Можно посмотреть, как решает задачу лучшее решение среди участников олимпиады ("Председатель жюри" из ИТМО):

• короткое видео на маленьком тесте: https://www.youtube.com/watch?v=EGvCS41Ucs4
• длинное видео с решением большого теста: https://www.youtube.com/watch?v=gOdXv21AcKs

9. Решающий удар

Для определения вероятности посчитаем динамику
    v[n][d] — количество исходов при бросании n игральных костей,
              при которых сумма результатов равна d.

База динамики
Для первой кости и каждого из исходов 1 <= d_roll <= f
    v[1][d_roll] = 1.

Переход динамики
Уже бросили (n - 1) кость и сумма результатов равна d,
бросаем ещё одну кость и выбрасываем на ней d_roll, тогда
    v[n][d + d_roll] увеличивается на v[n - 1][d].
При добавлении очередной кости суммируем по всем d и d_roll.

Количество нужных нам исходов получаем суммой
    S = sum v[n][d], max(1, D - m) <= d <= n * f.

Итоговая вероятность равна
    S / f^n.

7. Планировщик

Пусть X[i] = P[i] + T[i].

В задаче нужно выбирать среди N значений X[i] минимальное — для этого отлично подойдёт бинарная куча.
Кроме того, нужно на каждой итерации прибавлять единичку ко всем X[i] (кроме одного).
Чтобы этого не делать, давайте договоримся, что будем хранить в программе Y[i] = X[i] — t, где t — сколько секунд прошло с начала работы планировщика.
В этом случае прибавление единички ко всем X[i] происходит автоматически благодаря тому, что мы увеличиваем t после каждой итерации.

Решение заключается в том, чтобы хранить и поддерживать Y[i] для всех процессов в бинарной куче.
На каждой итерации нужно выбрать процесс с минимальным значением Y[i], и присвоить ему Y[i] := P[i] — (t+1), обновив его положение в куче.
Чтобы среди процессов с равным приоритетом выбирался процесс с минимальным номером, можно хранить в куче на максимум пары (Y[i], -i) с лексикографическим сравнением.

Разумеется, свою бинарную кучу писать не обязательно.
В C++ для этого есть push_heap/pop_heap, priority_queue и set, а Java есть TreeSet.

5. Леспромхоз

Область, в которой может находиться машина, чтобы захватить конкретное дерево — это кольцо с радиусом от H — R до H + R (центр в P).
Нужно найти точку, которая попадает в максимальное количество колец.

Легко заметить, что оптимальный ответ будет среди таких точек:
  1) точки пересечения граничных окружностей
  2) по одной произвольной точке на каждой окружности
Доказывается так: рассмотрим оптимальную точку, если она не такая, будем двигать её или куда угодно, или по окружности, и получим такую точку с кратностью не хуже.
Всего O(N^2) пробных точек, каждая проверяется влоб за O(N).
Получаем решение за O(N^3).

3. Найти радистку

Сделаем два запроса:
? -10000 -10000 1 0
? -10000 -10000 0 1
Поскольку координаты цели небольше 1000 по модулю, цель точно расположена строго между ними.
Отношение уровня сигнала этих двух запросов даёт тангенс угла между осью координат и направлением на цель.

Затем можно сделать аналогичные два запроса из точки (-10000, 10000), например.
В результате получится два луча, которые гарантированно не параллельны.
Находим точку пересечения и округляем — это и будет положение цели.
Хватает 5 запросов, считая последний запрос на попадание в цель.

6. Кеширование приближений

Прежде всего, для каждой операции вместо данного tol посчитаем L — минимальный размер подходящего приближения:
  L = S * pow(1/tol, 0.25)
Теперь получается, что для операции нужно иметь приближение размера M >= L, при этом тратится время C * M + D.
На построение приближения размера M тратится A * M + B времени — сложных формул больше нет.

В варианте 1, когда кеширование отключено, для каждой операции надо строить приближение заданного размера L.
Что-то более точное строить смысла нет — всё равно на выброс.
Тогда ответ равен:
  ans =   sum { (A * L[i] + B) + (C[i] * L[i] + D[i]) }
        i=1..n


В варианте 2 можно хранить только одну кривую.
Нужно разбить все n операций на отрезки, такие что на каждом отрезке используется своё приближение, а между отрезками приближение перестраивается.
Запишем ДП:
  R[i] — минимальные затраты времени, чтобы а) покрыть первые i операций описанными выше "отрезками"
  (0 <= i <= n)                               б) выполнить первые i операций, так что перед i-ой операции приближение будет выброшено/перестроено

Рекуррентная формула пишется по достраиванию последнего "отрезка" от R[j] до R[i].
Очевидно, для него надо брать допустимое приближение минимального размера Hij:
  Hij =    max   L[k]
        k=j..i-1
При этом на построение этого приближения и на выполнение с ним всех операций на отрезке потребуется:
  Tij = (A * Hij + B) +   sum  (C[k] * Hij + D[k])
                        k=j..i-1
С этими значениями общая формула записывается так:
  R[i] = min (R[j] + Tij)
         j < i
Значения Hij и Tij можно довычислять за O(1) внутри цикла по j.
Получается решение за O(N^2) времени и с O(N) памяти.


В варианте 3 можно хранить сколько угодно приближений в кеше.
Легко понять, что в таких условиях можно построить все приближения заранее, а потом для каждой операции выбирать самое маленькое подходящее.
Следовательно, от порядка операций ничего не зависит: давайте отсортируем их по возрастанию размера L[i].
Теперь для первых операций используется первое приближение, затем в какой-то момент переключаемся на второе, затем на третье, и т.д.
То есть по сути после сортировки в кеше можно хранить только одно приближение, а значит задача свелась к предыдущей.

Запускаем в точности динамику из варианта 2, только после предварительной сортировки по L[i].
В ответ выводим, что все построенные приближения надо построить сразу, до первой же операции.

4. Код Морзе

Разобъём сигнал на элементы — отрезки одинаковых значений.
Будем решать динамикой, читая элементы по очереди.

Состояния динамики:
  R[k] — минимальное количество ошибок при расшифровке префикса из k элементов в полные слова
Переход — выбрать любое слово в словаре и добавить его.
При этом надо наложить закодированный вид слова на продолжение сигнала и посчитать количество ошибок.
Т.к. каждое слово из каждого состояния обрабатывается примерно за его длину, получаем:
  Память: O(N)      (N — количество элементов)
  Время: O(N D)     (D — суммарный размер словаря)

На самом деле, легко заметить, что если сигнал можно расшифровать, то количество ошибок при любом варианте расшифровке получается одинаковое.
Так что существенная часть задачи — это выбор лекс. минимального варианта текста.
Чтобы его найти, можно традиционно запустить динамику в обратном направлении:
  R[k] — минимальное количество ошибок при расшифровке суффикса, начинающегося с k-ого элемента, в полные слова
Переходы надо делать в сторону уменьшения k, и для каждого состояния сохранять лекс. минимальное слово, по которому в него пришли.
Тогда обратный ход восстановит лексикографически минимальный ответ.

Стоит заметить, что на многих тестах в этой задаче отлично работают всякие переборы с отсечениями.
Можно построить класс тестов, которые эквивалентны задаче о рюкзаке, ставя четыре минуса между одинаковыми буквами и задавая слова из той же буквы разной длины.
На таких тестах переборы работают плохо, так что хочется верить, что исчезающе мало переборов получило Accepted =)

8. Текстовый редактор

Если разобраться в механике процесса, то получается, что план должен состоять из 1) перемещений вверх/вниз и 2) переноса куска текста.
При переносе определяется, до какой позиции от текущий надо выделить кусок, и в какое именно место вставить.

Поскольку N довольно маленькое, можно решить задачу "влоб".
Составим граф состояний и переходов.
Состояние — это порядок строк текста плюс текущее положение курсора. Всего (N+1)! состояний (N = 8 -> 362880 штук).
Переходов из каждого состояния порядка O(N^2) — нужно перебрать две позиции. (N = 8 -> примерно 30 штук)
Далее на этом графе можно запустить алгоритм Дейкстры с кучей, получив решение за O((N+1)! * N^2 * N).

Концептуальных сложностей в этом нет, однако в задаче довольно жёсткие требования по скорости работы.

Поэтому нужно применить следующие оптимизации:
  1) Вместо того, чтобы складывать все состояния в map/dictionary, можно их все честно закодировать номерами от 0 до (N+1)!-1.
  2) Поскольку все расстояния и тайминги очень маленькие, то в алгоритме Дейкстры вместо кучи можно использовать набор списков.
    То есть для каждого числа k = 0..5000 хранить список всех вершин v, у которых D[v] = k.
  3) Порядок строк не влияет на структуру переноса, поэтому можно предподсчитать все переносы для каждого положения курсора.
    Получится O(N^3) переходов, для каждого можно заранее сохранить перестановку строк, стоимость, новое положение курсора.


В принципе, можно дополнительно оптимизировать алгоритм с помощью эвристики A*, хотя для получения Accepted это было НЕ обязательно.

Для этого нужно построить функцию оценки снизу расстояния до конечного состояния.
Пусть D элементов находятся не на своём месте.
Тогда необходимо сделать как минимум D нажатий клавиш вверх или вниз, чтобы "замести" эти строки — иначе не получится их изменить.
Теперь найдём "разрезы" — такие положения, что строка снизу и строка сверху в конечном состоянии НЕ должны тоже идти подряд в том же порядке.
Каждое наше перемещение режет текст в трёх местах и сшивает по-другому, а значит устраняет максимум три разреза.
Поэтому если есть K разрезов, то нужно как минимум roundup(K/3) перемещений, в каждом из них нужно нажать по одному разу все клавиши/комбинации кроме вверх/вниз.
Получается оценка:
  H(v) = D * min(Tup, Tdown) + roundup(K/3) * (Tshpr + Tshrel + Tctrlx + Tctrlv)
Можно показать, что эта оценка монотонная, то есть с ней алгоритм A* эквивалентен алгоритму Дейкстры с потенциалами, и все модифицированные веса неотрицательные.

2. Антиталия

Будем решать задачу методом движущейся плоскости: будем считать, Z-координату сечения "временем", и смотреть, как изменяется сечение.
В сечении всегда получается набор контуров (внешних/внутренних), ограничивающих плоскую область (или несколько плоских областей).
По мере увеливения Z структура контуров сохраняется, а точки в контурах движутся с некоторой скоростью — пока секущая плоскость не пройдёт через какую-нибудь вершину триангуляции.
Прохождение плоскости через вершину будем считать событием и обрабатывать особо.

В отличие от простых задач, где ответ всегда совпадает с каким-нибудь событием, в этой задаче оптимальное сечение может произойти между событиями (см. пример 2).
Заметим, что с течением времени (t = Z) каждая точка контура в сечении движется с постоянным вектором скорости, то есть координаты точек линейно зависят от времени.
Поскольку площадь контура считается как полусумма cross(P[i], P[i+1])/2, то получается, что площадь сечения зависит от времени квадратично.
Если для конкретного интервала между соседними событиями посчитать площадь как квадратичную функцию от Z, то найти её максимум на интервале будет легко:
надо лишь проверить значение в начале и в конце, а также в вершине параболы, если она находится внутри интервала.

К сожалению, отслеживать контуры в сечении очень сложно: контуры возникают, объединяются, разделяются и т.п.
На самом деле, это и не нужно: вклад каждого отрезка сечения в площадь сечения никак не зависит от окружающих объектов.
Действительно, каждый отрезок P->Q сечения добавляет cross(P, Q)/2 в общую площадь — главное верно определить направление отрезка, т.к. от этого зависит знак площади.
Оказывается, если сторона треугольника пересекает плоскость сверху вниз (т.е. Z убывает), тогда точка пересечения будет началом отрезка сечения, порождённого этим треугольником.
Другая сторона треугольника, которая пересекает плоскость снизу вверх (Z возврастает), будет концом этого отрезка.
Третья сторона в сечении отсутствует: они либо полностью сверху, либо полностью снизу плоскости.
Разумеется, здесь подразумевается, что стороны направлены в порядке обхода, указанном в файле.

Таким образом, получается довольно простое решение.
Выпишем все события (т.е. вершины сетки) в один большой массив, отсортируем их по времени.
Далее обрабатываем события по порядку, все одновременные события обрабатываем одной группой.
Сначала для всех треугольников, инцидентных всем вершинам в текущей плоскости, "выключаем" старый отрезок, а затем для всех этих же треугольников считаем и "включаем" новый отрезок.
Вклад каждого отрезка-треугольника в площадь лучше хранить в массиве, тогда выключение — это просто зануление соотв. элемента этого массива.
При включении нужно представить, что секущая плоскость чуть выше рассматриваемой плоскости, понять, как устроен отрезок сечения, и посчитать векторное произведение движущихся точек.
Разумеется, если треугольник/отрезок уже включен, то включать его повторно не надо, чтобы не учесть его вклад в площадь дважды.
Текущую площадь как квадратичную функцию можно хранить в глобальной переменной: при выключении отрезка вычитать его старую функцию, а при включении добавлять новую функцию.

Если предподсчитать списки инцидентных вершинам треугольников заранее, то весь алгоритм будет работать за O(N log N).


Одна из проблем этой задачи — точность при работе с квадратичными функциями (коэффициенты которых никак не целые).
При желании почти любое решение можно завалить по точности, сделав соответствующий тест.
При подготовке задачи все проблемные тесты были выброшены, а требование точности было выставлено так, чтобы все правильные решения проходили с запасом (все они используют тип double).

Тем не менее, есть ряд способов кардинально улучшить точность решения в разных ситуациях (ни один из них НЕ был нужен, чтобы получить Accepted):
1) Хранить квадратичные функции для треугольников не в обычном массиве, а в дереве отрезков на сумму, при изменении честно пересчитывая все узлы до корня.
  Это позволяет полностью избежать накопления погрешности, а кроме того снижает погрешность суммирования в целом (см. https://en.wikipedia.org/wiki/Pairwise_summation).
2) Вычислять для отрезка cross(P, Q-P) вместо cross(P, Q): помогает для тонких тел вдали от начала координат по X/Y.
3) Вычислять квадратичные функции не от переменной Z, а от смещения (Z — O), где O — это например Z-координата вершины треугольника, при рассмотрении которой вычислялась эта функция.
  Это сильно повышает устойчивость представления квадратичных функций для коротких по Z треугольников на большом расстоянии от Z == 0.
  Правда при сложении функций с разными O в дереве отрезков нужно делать дополнительную конвертацию.

7. Придорожная оптимизация

Для каждого теста нужно вывести число рёбер в лесе: количество вершин — число компонент связности. Поскольку в условии дана матрица достижимости (уже транзитивно замкнутая матрица смежности), то ответ можно найти проходом по матрице. Например, посмотреть на значения в позиции i, j над главной диагональю: если стоит 1 и индекс j ещё не использован, то увеличить ответ на 1 и пометить индекс j как использованный.

6. Дробь

Задача сводится к тому, что для запроса (знаменателя) $$$X$$$ нужно найти ближайшее $$$X_0$$$ ($$$X_0$$$ >= $$$X$$$) такое, что в системе счисления $$$B$$$ дробь $$$1/X_0$$$ конечная. Введем функцию $$$F(a)$$$ — множество различных простых чисел в факторизации числа $$$a$$$. Тогда, $$$X_0$$$ подходит к ответу, если $$$F(X_0)$$$ является подмножеством $$$F(b)$$$, то есть в разложении $$$X_0$$$ используются только те простые, которые используются в разложении $$$b$$$.

Предпосчитаем для заданного $$$B$$$ всевозможные $$$X_0$$$ в массив $$$V$$$, отсортировать их. Дальше для ответа на запрос нам нужно найти ближайшее число, которое больше или равно числу из запроса. Это можно сделать либо бинарным поиском, либо двумя указателями.

Всевозможные $$$X_0$$$ ищутся рекурсивным перебором. Следует заметить, что нужно аккуратно проверять при домножении на очередное простое, что произведение не превысит $$$M$$$.

5. Починка кучи 32-бит

Заметим, что всегда можно записать в первую и последнюю ячейки N-2, получив правильную кучу с 2 изменениями. Значит надо лишь определить, является ли куча корректной, и можно ли получить корректную за одно изменение.

Запустим два прохода по блокам кучи, предполагая кучу корректной. При проходе вперёд читаем слово из следующей ячейки, и прыгаем вперёд на это число плюс 2. При проходе назад симметрично. Если ошибок нет, тогда оба прохода закончатся за 25K шагов, и блоки будут одинаковые в обе стороны. Если ошибка одна, тогда один проход пройдёт по корректной куче, показав, какими должны быть блоки.

Когда сделаем оба прохода (с ограничением 25К на количество шагов), каждый успешный проход надо провалидировать. То есть проверить размеры с другой стороны — если ошибка только одна, то печатаем решение.

9. Плащ и ружьё

Допустим, мы влетаем в некоторую клетку сверху. Найдём ближайшую к ней клетку с почвой слева и справа. Отрезок между ними является для нас рабочим: мы можем убить всех монстров на нём, и вылететь из отрезка вниз в любой его точке.

Разобъём весь уровень на такие горизонтальные отрезки. Отрезок с буквой S — начальный, с буквой E — конечный. Из произвольного отрезка можно перейти в любой отрезок на следующей горизонтали, который граничит с текущим по стороне хотя бы одной клетки.

Так можно построить граф отрезков: вершины — монстры, рёбра — как можно переходить в следующему отрезку. В каждой вершине запишем количество монтров на отрезке. Нужно найти путь, на котором сумма чисел максимальна. Это легко решается динамическим программированием, т.к. граф без циклов:

• R[s] — какую максимальную сумму можно набрать, пролетев из начала в отрезок s.

Время работы — линейное от площади карты.

10. Остап и стулья

Каждая функция под суммой в зависимости от k и b — выпуклая и кусочно-линейная. Значит и функция полного расстояния будет тоже выпуклой и кусочно-линейной. То есть если её нарисовать как график D(k, b), то это будет низ некоторого выпуклого многогранника. Рёбра многогранника — это линии излома, вдоль которых верно Xi = k * Yi + b. Очевидно, минимум такой функции достигается в какой-то вершине, а любая вершина получается на пересечении двух рёбер.

Получается простое решение за O(N^3): берём все линии Xi = k * Yi + b и пересекаем их попарно, находя точки в (k, b)-плоскости. Делается это очень легко, т.к. никаких параллельностей и совпадений в этой задаче быть не может. Каждую точку проверяем, вычисляя функцию влоб.

Альтернативное решение — написать двумерный тернарный поиск. Грубо и кода больше, но при достаточном количестве итераций работает.

4. Починка кучи 8-бит

Будем решать задачу динамикой:

• R[p] — минимальное количество исправлений, чтобы сделать префикс в p ячеек правильной кучей.

Обозначим массив ячеек памяти через A. Получается рекуррентная формула:

• R[p] = min{x=2..257} (R[p-x] + (A[p-x] != x-2) + (A[p-1] != x-2))

Здесь неравенства в скобках дают единицу, когда они верны, и ноль иначе.

Ускорим решение следующим образом. Нарисуем из каждой ячейки:

• ребро вперёд i -> i + A[i]
• ребро назад i -> i — A[i-1]

Заметим, что при стоимость перехода (p-x -> p) в описанной выше ДП равна: 2 минус количество рёбер между p-x и p. Если между состояниями нет рёбра ни в одну сторону, то стоимость 2. Если ребро есть в обе стороны, то стоимость 0. Если только в одну, то стоимость 1. К счастью, рёбер всего только 2N.

Тогда при вычислении R[p] будем сначала считать минимум, предполагая переходы стоимости 2:

• R[p] = ( min{x=2..257} R[p-x]) + 2 //вычисляется за O(1)

Минимум обновляется за O(1), если хранить в очереди все элементы, которые могут стать минимумом в будущем. Далее будем явно перебирать рёбра из p (оно одно), и рёбра в p (надо заранее сложить развёрнутые рёбра назад), и вычислять переход влоб. Всего таких особенных переходов будет 2 N штук.

Получается решение за O(N). В задаче также требуется использовать мало памяти. Достаточно хранить входные данные, а также обратный ход динамики как массив байтов — это требует 2 N байтов памяти. Все остальные данные можно хранить только для текущего окна из 256-512 элементов, так что затраты памяти на них пренебрежимо малы.

3. Бомбы

Разрешим закладывать сколько угодно бомб перед детонацией. Можно доказать, что тогда минимальное требуемое количество детонаций будет таким же, как минимальное требуемое количество бомб в исходной задаче.

В решении потребуется выполнять операцию, которая в обработке изображений называется dilate. Формулируется она так: допустим есть множество клеток X, в которые мы заложили бомбы. Какие клетки будут затронуты взрывами?

В ходе решения будем поддерживать достижимое множество клеток, постепенно расширяя его. Сначала найдём все достижимые из S клетки (обход по пустым клеткам). Затем заложим в них всех бомбы, и расширим множество с помощью операции dilate. Далее из всех клеток, освобождённых взрывами, снова запустим обход и найдём всё новые достижимые по пустоте клетки. Теперь заложим бомбы во всех клетках, которые освобождены предыдущим взрывом, и в клетках, найденных обходом после этого. Сделаем dilate, далее снова расширим множество по достижимости по пустым клетками, и так далее.

В общем случае, на каждой фазе мы закладываем бомбы во всех клетках, которые достижимы, и в которых не закладывали бомбу раньше. После этого запускаем поиск новых достижимых клеток, причём запускаем его только из тех клеток, которые были освобождены от земли последним взрывом. Благодаря этому в каждой клетке бомба закладывается не более одного раза, а обход по пустым клеткам запускается максимум один раз. В таком виде решение работает за O(M N * R^2), и большую часть времени съедает операция dilate.

Благодаря специальной форме взрыва, можно выполнить операцию dilate быстрее, разбив её на несколько шагов. Допустим, бомбы заложили в множестве X. Тогда можно заметить, что множество затронутых взрывом клеток — это все клетки, достижимые из X после:

1. R переходов первого типа (переход разрешён в соседнюю по стороне клетку) и
2. P/2 переходов второго типа (переход разрешён в любую из восьми соседних клеток)

Поэтому при выполнении операции dilate в алгоритме можно делать R + P/2 шагов. После каждого шага будет "волна" новых достижимых клеток — как в "волновом" алгоритме, который иногда рассказывают вместо аналогичного BFS.

Изначально есть волна X — те клетки, где мы заложили бомбу. На каждом шаге мы перебираем все клетки последней волны, и просматриваем их соседей нужного типа. Если соседняя клетка ещё не достижима в алгоритме, тогда помечаем её как достижимую и добавляем в следующую волну. За R + P/2 таких шагов мы расширим достижимое множество на общую область взрыва.

Заметим, что в таком алгоритме каждая клетка просматривается O(1) раз. Тогда общее время работы O(M N).

8. Деревянный трубопровод

Если c(f) — минимальная стоимость потока размера f в сети, то известно, что c(f) — некоторая выпуклая кусочно-линейная функция. Мы будем запускать обычную динамику по дереву, и для каждого v-поддерева вычислять функцию c(f) для потока из корня поддерева v в листья поддерева.

Раз c(f) является ломаной (выходящей из начала координат), будем хранить её как ломаную. Чтобы это работало быстро, будем хранить последовательность отрезков (в порядке слева направо). Для каждого отрезка будем хранить:

1. "длину" отрезка вдоль координаты f (т.е. вдоль оси абсцисс)
2. "наклон" — т.е. производную dc/df вдоль отрезка

Более того, будем хранить эти отрезки в дереве поиска, ключ = наклон.

Чтобы пересчитывать динамику, надо уметь делать две вещи.

1. Если известна функция c(f) для v-поддерева, надо уметь добавлять ребро vp, идущее из корня наверх. Для этого нужно сначала обрезать c(f) по capacity(pv) — больше поток быть никак не может. Это делается выбрасыванием всех вершин с бОльшим f, и добавлением вершины с f = capacity(pv) с бесконечным наклоном. Далее надо прибавить к функции c(f) линейную функцию cost(pv) * f — это делается добавлением cost(pv) к наклону всех вершин.
2. Если известна функция c(f) для двух поддеревьев с общим корнем v, нужно суметь их объединить. Легко заметить, что результат можно получив, слив две функции c(f) как упорядоченные последовательности (сравнивая по наклону), однако это медленно. Вместо этого, надо взять функцию с меньшим количеством отрезков, и вставить все её отрезки по одному в бОльшую функцию.

Как добавлять сразу к наклонам всех отрезков дерева? Видимо, достаточно хранить одно значение "добавка к наклону всех отрезков" вместе с каждым деревом.

Изменение 1 делается за O(K log N), где K — количество удалённых вершин. Заметим, что вершины добавляются только при обрезании по проп. способности ребра, это делается N-1 раз. Значит в сумме это даёт O(N log N). Изменение 2 делается за O(A log B), где A — меньший размер, а B — больший размер при слиянии. Известно, что в таком случае по всему дереву будет время O(N log^2 N).

Альтернативное решение — найти всё, что нужно, методом дополняющих путей — как обычно. Каждый дополняющий путь идёт из корня в лист. Можно их все выписать, отсортировать по стоимости, брать по одному и проталкивать.

Чтобы протолкнуть по пути, надо:

1. Найти минимум проп. способностей рёбер от листа до корня.
2. Вычесть из всех проп. способностей рёбер от листа до корня заданное число (найденное в п.1).

Это можно сделать с помощью heavy/light декомпозиции. На каждом heavy-отрезке надо хранить дерево отрезков на минимум с возможностью прибавления на отрезке. Получается тоже O(N log^2 N)

Привет, Codeforces!

Скоро начнётся XXI Открытая Всесибирская олимпиада им. И. В. Поттосина — соревнование по программированию, в котором принимают участие студенты вузов со всей России, а также стран СНГ.

Олимпиада состоит из отборочного и очного финального этапов. Отборочный этап (известный также как "интернет-тур") проходит через интернет в формате ICPC, и участвовать в нём могут все желающие команды. Основной язык олимпиады, на котором написаны условия задач и происходит общение с жюри, — русский. В этом году финальный этап будет проходить в режиме онлайн, участникам не придётся ехать в Новосибирск. При отборе команд в финал для команд от Сибири и Дальнего Востока выделяется квота не менее 50% от общего числа финалистов.

Традиционная для всесибирской олимпиады "первая номинация" в этом году не планировалась. На текущий момент сложно сказать точно, будет она или нет. Совершенно точно будет финальный раунд по правилам ICPC-олимпиад: 8-12 задач, на решение которых отводится 5 часов. Более подробно правила и положение олимпиады можно прочитать здесь.

Отборочный тур состоится в воскресенье, 27 сентября, в 10:00 по московскому времени. Очный тур пройдёт с 31 октября по 2 ноября. Параллельно с отборочным соревнованием на этом же наборе задач будет проходить этап Открытого Кубка. Команды, желающие участвовать в отборочном раунде и бороться за выход в финал, должны регистрироваться и писать контест в системе тестирования NSUts. Остальные команды, желающие просто написать контест, могут решать его как обычный этап Открытого Кубка.

Регистрация в системе тестирования открыта здесь. После регистрации можно порешать пробный тур. В отборочном раунде планируется задача с бинарным вводом/выводом, поэтому рекомендуется решить задачу "4. Сумма Чисел" из пробного тура.

UPDATE: Разбор задач опубликован здесь. Дoрешивание открыто в nsuts в олимпиаде "Тренировки". Кроме того, если у вас есть логин opencup-а, можно дорешивать там те же задачи как Гран-При Евразии.

UPDATE: В финальном раунде будет две номинации, обязательно участие в них обеих. На первой номинации будет одна большая задача на 5 часов, а на второй номинации — традиционный контест по правилам ICPC. Результаты двух номинаций будут суммироваться для получения итоговых результатов всей олимпиады. Правила суммирования будут объявлены на открытии.

В этом году на Всесибирской олимпиаде участникам предложили поиграть в стрелялку. Игра была однопользовательская: каждый участник писал свою программу и набирал очки в игре независимо от остальных участников. Наверное играть всем скопом интереснее, чем играть поодиночке. Зато теперь в стрелялку могут поиграть все желающие, для этого им не нужно быть в Новосибирске и очно соревноваться. В целом, идея однопользовательской игры повторяет первый тур 2010 года (который был по игре crimsonland).

Жанр игры: вертикальный скролл-шутер. Имеется квадратное игровое поле, на котором расположен самолёт игрока, а также появляются разные летающие враги. Игрок и враги могут стрелять, в результате чего по полю также летают снаряды. Игрок может стрелять только вверх, при этом большая часть врагов движется вниз. Столкновение с чужим снарядом наносит урон как игроку, так и врагу. Игрок может таранить врагов: при этом ему также наносится урон. Игроку даются очки за уничтожение врагов и за прохождение уровней.

Видео игры с простым решением, которое доходит до первого "босса" (без спойлеров).

Видео, на котором решение жюри проходит всё игру (спойлеры!):

Архив материалов можно скачать по этой ссылке.

Если у вас есть винда, то можно распаковать и спокойно решать: условие задачи включено. Учтите, что для решения на Python и Java нужно точно те же версии, которые стояли на месте проведения (см. readme.md).

Привет, Codeforces!

Скоро начнётся XX Открытая Всесибирская олимпиада им. И. В. Поттосина — соревнование по программированию, в котором принимают участие студенты вузов со всей России, а также стран СНГ. В этом году у нас юбилей =)

Олимпиада состоит из отборочного и очного этапов. Отборочный этап (известный также как "интернет-тур") проходит через интернет в формате ICPC, и участвовать в нём могут все желающие команды. Основной язык олимпиады, на котором написаны условия задач и происходит общение с жюри, — русский. В очный этап проходит ориентировочно 50 команд, при этом для команд от Сибири и Дальнего Востока выделяется квота не менее 50% от общего числа участников очного тура.

Очный этап традиционно состоит из двух туров. Один из них проходит по правилам ICPC-олимпиад: 8-12 задач, на решение которых отводится 5 часов. На другом туре участникам предлагается решать одну "большую" задачу в течение 5 часов. Тематика задач такого тура разнообразна: игровые задачи на написание AI (пример), не имеющие идеального решения задачи, было даже параллельное программирование. Более подробно правила и положение олимпиады можно прочитать здесь.

Отборочный тур состоится в воскресенье, 29 сентября, в 10:00 по московскому времени. Очный тур пройдёт в Новосибирске с 1 по 4 ноября. Параллельно с отборочным соревнованием на этом же наборе задач будет проходить этап Открытого Кубка. Команды, желающие участвовать в отборочном раунде и бороться за выход в очный тур, должны регистрироваться и писать контест в системе тестирования NSUts. Остальные команды, желающие просто написать контест, могут решать его как обычный этап Открытого Кубка.

Регистрация в системе тестирования открыта здесь. После регистрации можно порешать пробный тур. Настоятельно рекомендуется решить задачу "3. Сумма Чисел" из пробного тура.

В этом году в первой номинации Всесибирской олимпиады участникам снова предлагалось написать программу управления роботами-пылесосами.

Как и в прошлом году, игра массовая: в каждой игре запускаются вместе стратегии всех 46 команд. Поэтому, как и в прошлом году, участником пришлось писать стратегии на языке Lua. По появившейся в прошлом году хорошей традиции, в каждом классе, в котором писали соревнование участники, был включен телевизор или проектор, на котором постоянно по циклу показывались последние игры, прошедшие на сервере жюри. Это позволяло участникам быстрее и проще адаптировать свои стратегии под изменения стратегий соперников. Более того, каждый участник мог даже скачать решения всех других участников в любой прошедшей игре, и запустить их локально в любых желаемых конфигурациях.

Правила игры были довольно простые. У каждого игрока есть пылесос, который ездит по полю, и своя территория. Когда пылесос ездит вне своей территории, он оставляет за собой хвост. Если пылесос замыкает свой хвост, вернувшись на свою территорию, тогда все клетки замкнутого контура переходят к нему. Если в хвост пылесоса кто-либо врезается, то игрок умирает: его пылесос, хвост и территория исчезают. Поле циклически замкнуто по горизонтали и вертикали. В качестве очков игрока бралась максимальная достигнутая в течение игры площадь своей территории, к тому же был бонусный множитель за убийства.

Видео одной игры финального тестирования.

Сейчас по задаче можно скачать:

1. Исходные коды игры. Для сборки нужны CMake и Qt, но дорогу осилит идущий =)

2. Оригинальные материалы. Этот архив выдавался участникам на соревновании. В нём есть в том числе полное условие задачи и виндовые бинарники. Если визуализатор сходу не запускается, советуем собрать из исходников.

.

.

Немного фото с места проведения:

В этом году в первой номинации Всесибирской олимпиады участникам предлагалось написать программу управления роботами-пылесосами.

Существенным отличием от прошлых лет стало то, что игра по сути своей массовая, а не одиночная (пример 2010 года) или дуэльная (пример 2013 года). В каждой игре участвуют одновременно все соревнующиеся 50 команд. Каждый игрок управляет 10 роботами, которые бегают по круглому полю. Если робот набегает на другого робота меньшего размера (или на пассивную неподвижную "еду"), то он его съедает, увеличивая свою площадь на площадь съеденного объекта. Кто съел всё (а это гарантированно происходит из-за сужения игрового мира) — тот победил. Для произвольного игрока очки за игру определяются по суммарной площади его роботов в наилучший для него момент времени. С ростом робота его скорость снижается, поэтому в игру добавлен "турбо-режим", позволяющий периодически удваивать скорость на короткое время.

Чтобы исключить технические проблемы при одновременном запуске 50 решений, решено было ограничить соревнование одним языком программирования — языком Lua. Это не первый раз, когда нам приходится потребовать от участников использовать этот незнакомый для них язык. Игра запускается в одном процессе ОС, а каждый игрок работает в своём закрытом Lua-состоянии. В результате можно запускать игру с 50 игроками в реальном времени даже на одном обычном компьютере.

Во время тура игра запускалась по циклу примерно каждые три минуты. Каждый раз в игре участвовало по одному самому новому решению от каждой команды. Примерно с середины тура в классах подняли показ результатов последней игры (в цикле) на проекторе или на большом телевизоре. В комнате жюри у телевизора постоянно паслись болельщики, выглядело это примерно так:

Конечно, интереснее всего было смотреть игры в середине тура, когда стратегии участников сильно менялись. В течение какого-то времени эти игры можно будет скачать с сервера, например при помощи скрипта download.bat. Вот видеозаписи некоторых игр (youtube-плейлист со всеми играми; видео в хорошем качестве можно скачать отсюда):

1. Через час после начала тура: прогон 100

2. Через два часа после начала: прогон 150

3. Через три часа после начала: прогон 175

4. Через три с половиной часа после начала: прогон 200

5. Через четыре с половиной часа после начала: прогон 230

6. После конца тура: прогон 256

Сейчас по задаче можно скачать:

1. Полный архив: исходный код игры, решения участников, виндовые бинарники.

2. Материалы: только виндовые бинарники.

Привет, Codeforces!

В этом году состоится XVII Открытая Всесибирская олимпиада им. И. В. Поттосина — соревнование по программированию, в котором принимают участие студенты вузов со всей России, а также стран СНГ.

Олимпиада состоит из отборочного и очного этапов. Отборочный этап (известный также как "интернет-тур") проходит через интернет в формате ACM, и участвовать в нём могут все желающие команды. Основной язык олимпиады, на котором написаны условия задач и происходит общение с жюри, — русский. В очный этап проходит ориентировочно 50 команд, при этом для команд от Сибири и Дальнего Востока выделяется квота не менее 50% от общего числа участников очного тура.

Очный этап традиционно состоит из двух туров. Один из них проходит по правилам ACM-олимпиад: 8-12 задач, на решение которых отводится 5 часов. На другом туре участникам предлагается решать одну "большую" задачу в течение 5 часов. Тематика задач такого тура разнообразна: игровые задачи на написание AI (пример), не имеющие идеального решения задачи, параллельное программирование. Более подробно правила и положение олимпиады можно прочитать здесь.

Отборочный тур состоится в воскресенье, 2 октября, в 11:00 по московскому времени. Очный тур пройдёт в Новосибирске с 4 по 7 ноября. Параллельно с отборочным соревнованием на этом же наборе задач будет проходить этап Открытого Кубка. Команды, желающие участвовать в отборочном раунде и бороться за выход в очный тур, должны регистрироваться и писать контест в системе тестирования NSUTs. Остальные команды, желающие просто написать хороший контест, могут решать его как обычный этап Открытого Кубка. Регистрация в системе тестирования открыта здесь (форма регистрации пока переживает не лучшие времена, но мы всё ещё работаем над этим).

UPDATE: Прошу прощения у всех тех, кто решал контест в системе тестирования nsuts, за малоприятные пять часов жизни. Могу лишь надеяться, что не все пять часов были потрачены зря. Также хочу извиниться за отсутствие ответов на вопросы об очереди и проблемах тестирования.

Сейчас рейтинг разморожен. Дорешивание в nsuts открыто в олимпиаде "Тренировки", в туре "Интернет-тур Всесибирской олимпиады (2016): дорешивание". Чуть более подробная инструкция среди ответов на вопросы в самом интернет-туре. Кроме того, многие из вас могут дорешивать задачи в Открытом Кубке (GP of Eurasia).

Доброго времени суток!

Добавил в тренировки Codeforces интернет-тур Всесибирской олимпиады по программированию имени Поттосина (этого года). Условия задач решил оставить оригинальными, поэтому пришлось перенести все оповещения-уточнения из оригинального тура.

Если кто-то не принял участие в самом соревновании, приглашаю порешать тренировку!

P.S. В принципе, дорешивать этот тур и/или решать его в режиме виртуального контеста можно и в тестирующей системе НГУ...

На первом туре предлагалось написать AI для простой стратегии. Есть заводы, они строят роботов. Роботы могут стрелять друг в друга и захватывать заводы. Каждый робот управляется автономным скриптом на LUA и видит только некоторую свою окрестность. При инициализации можно заложить какую-нибудь инфу в робота (например, куда идти), потом робот работает сам по себе.

Все материалы и логи/истории всех игр лежат здесь: http://parallels.nsu.ru:8080/finaltesting/

Сначала напишу, как посмотреть что-либо с первого тура тем, кто в нём не участвовал. Берём комп с виндой, качаем glut-визуализатор и распаковываем в какую-то папку. Потом берём из Logs\ какую-нибудь историю, например вот эту. Качаем её в ту же папку. Запускаем run_history.bat из этой папки. Должно запуститься проигрывание истории игры.

SFX-архив материалов, который выдавался участникам. Пароль: "armvscore" (без кавычек). Условие задачи есть внутри.

Чтобы материалы работали, нужно: 1. Консоль винды (канонически используется Far). 2. Visual С++ 32bit (>=2005) должен быть прописан в путях/переменных окружения (use vcvarsall.bat, Luke!). 3. Переменная JAVA_HOME должна быть установлена в папку с JDK 32bit (если хочется джаву). 4. В путях должен быть fpc.exe (если хочется паскаль).

Архива вполне хватает, чтобы писать решения. Там же исходники игрового сервера и вшитый дистрибутив LUA 5.1.5, скрипты для сборки всего этого.

UPDATE: Выложил на сервер окончательные решения всех команд (здесь). Также положил таблицу суммарных очков по первому туру.. И решение жюри, с которым играли ваши решения в течение тура.

P.S. Если кому-то понравилось, то можно перейти на более серьёзную игру. Утверждается, что в опенсорсной стратегии Zero-K можно писать LUA-скрипты для юнитов вплоть до полноценного AI игрока. Как время свободное будет, непременно проверю=)

Недавно включил тренерский режим Codeforces. Столкнулся с такой проблемой.

Есть тренировка, которую не я создавал. В ней есть задача. В этой задаче слабые тесты: проходит неправильное решение. Я хочу добавить один ручной тест, чтобы такое решение не проходило. И перетестировать решения по задаче не помешало бы...

Можно ли это сделать при помощи тренерского режима? Или самый простой способ — написать автору?

Я попробовал запустить Contest Wizard в режиме обновления этой задачи. Однако чтобы залить обновлённые материалы по задаче, нужно сначала где-то достать старые. Как получить старые — я не знаю. Получить доступ по FTP мне не удалось (как FTP-доступ сочетается с google-логином? двухфазной аутентификацией?).

Как известно, на первом туре всесибирской олимпиады участники писали бота для аркадной стрелялки, скопированной с реальной игры crimsonland. Так вот, немного помучавшись, я переписал клиентскую библиотеку C++-решений и приделал её к crimsonland-у. Теперь любое решение на C++ после недолгого переписывания можно заставить играть в crimsonland.

Например, в этом видео бот команды waterogers играет в rush:

http://www.youtube.com/watch?v=suwf-QYIrXI

А в этом видео решение жюри проходит один из уровней:

http://www.youtube.com/watch?v=KwSs1iqsGxg

Задача A: Ответ равен floor(N*M*0.5). Поскольку на доске N*M клеток, и каждая доминошка покрывает ровно 2 клетки, то больше положить точно нельзя. Теперь покажем, как положить ровно столько доминошек. Если N чётно, то кладём M рядов по N/2 доминошек и занимаем всю доску. Если N нечётно, то укладываем полностью (N-1) ряд доски как написано выше, а последний ряд забиваем floor(M/2) доминошками. При этом максимум останется одна незанятая клетка, в случае если N и M нечётны.

Добрый день.

Сегодня пройдёт ещё один раунд по правилам codeforces. Автором сегодняшнего контеста являюсь я. Раунд помогали готовить Артём Рахов и Мария Белова. Большое спасибо им и всем борцам фронта codeforces!

Желаю всем удачи и весёлых хаков!

P.S:  В связи с проблемами работы сервера раунд признан нерейтинговым. Приносим извинения всем участникам. Подробности в теме по этой ссылке.

Архив материалов первого тура всесибирской олимпиады 2010 года доступен для скачивания:

http://olimpic.nsu.ru/widesiberia/archive/wso11/2010/rus/arcade_full_archive.zip

Логи игр окончательного тестирования лежат отдельно.

В первом туре участникам предлагалось написать бота для простой аркадной стрелялки на манер crimsonland survival.