Hello Codeforces! It has been quite some time since I last wandered through these blogs :)
I was reading again just for fun about max flow and I remembered a thought I had back in my training days.
It is very common to use a modified version of Bellman-Ford to solve the min cost max flow problem, called Shortest Path Faster Algorithm (SPFA, you can read about it on books like Competitive Programming 3)
It is guaranteed this algorithm will end if the network doesn't have negative cycles, and here is where my question appeared.
In a network with capacity and nonnegative costs per unit of flow sent through an edge (or even a network with negative costs, but without negative cycles), how do you demonstrate there will be no negative cycle in the residual network? Even after sending flow and updating the network, there is no negative cycle reachable from the source that breaks the solution.
I never worried about negative cycles when implementing SPFA, but there are some algorithms that deal with these situations (like potentials, for example).
Thank you!








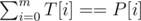 for every substring
for every substring 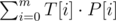 . This will give us the number of
. This will give us the number of 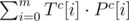
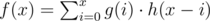
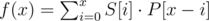
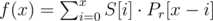 is equivalent to
is equivalent to 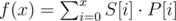
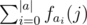 with
with