Hi everybody! I have been training these last months and I have learned a lot of things.
However, last weekend I came across with a problem that goes likes this:
There are N positions and N tokens (numbered from 1 to N, all distinct). There is a machine that moves the token that is in position i to position Pi. Initially the tokens are in the order 1, 2, 3, ..., N. The machine has a button that moves the tokens to the positions Pi's. After pushing the button for the first time, compute the number of times the button must be pushed in order to get all the tokens to their initial positions (Modulo 10^9 + 7).
For example, N = 4 and the Pi's are: 4 1 2 3 The answer is 4:
Initially — 1 2 3 4
Push 1: — 2 3 4 1 (Token 1 goes to position 4, Token 2 goes to position 1, ...)
Push 2: — 3 4 1 2
Push 3: — 4 1 2 3
Push 4: — 1 2 3 4
The maximum value of N is 10^6
I tried finding the disjoint cycles and computing the LCM of the lengths of them, but got TLE. Because of the modulo 10^9 + 7, the way I compute the LCM is obtaining the prime factorization of the lengths, keeping record of the maximum power of those prime factors, and multiplying them.
After receiving lots of Time Limit Exceeded verdicts I looked for help on the internet and found that this is a common Abstract Algebra problem called "The order of a Permutation Cycle".The answer is the LCM of the lenghts of the disjoint cycles :(
I don't know if my method is too slow or there are many test cases and the time limit is extremely strict... To compute the length of the cycles I use a simple adhoc algorithm. Iterate over all the Pi's, if some position is not visited, start the cycle until finding a position already visited. I used fast input to handle large test data, but didn't worked...
Thanks! :)
UPDATE: Here is my code
UPDATE 2: Finally accepted! Doing the factorization with smallest prime factors and better ways to handle the modular arithmetic were the key to pass the time limit! Thanks all specially user Jacob for pointing that out :)
The algorithm you described is correct, can you show the code? BTW, this problem on Timus (with small constraints)
Sorry for the waiting! I was adding some comments :) In order to avoid some memsets on boolean arrays, I mark an already processed number this way:
At every iteration of the program I use some integers as flags. If during iteration x a number has a flag of x+1, it means it is already processed, if not, process it and put a flag of x+1.
Here is the code
You can store smallest prime divisor in a sieve instead of just true/false. That should improve the factorization time.
Ok I submitted a code with that sieve but it seems the judge is offline -.-
Hope it get AC :)
Thanks! The smallest prime divisors and some mod optimizations did the trick :D
Hello!
The algorithm seems correct to me. However, I am curious: why do you need to do the prime factorization thing to compute the LCM? In particular, I thought you could compute lcm(a, b) = (a / gcd(a, b)·b) (mod p). And since the gcd is a divisor of a (by definition), you don't have to worry about finding inverses mod p (just be careful and use long long for the multiplication).
So you can compute lcm(a, b) in a quick operation. After this, use commutativity:
And you can repeat this to find the whole lcm of the sequence of numbers.
I could be mistaken, and the prime factorization should also work, but maybe this idea might shave off some time!
Commutativity won't really work because you can't compute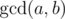
with only 
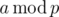and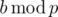 
known.
Ahh yes, my mistake! This is true. Thanks!
I tried that but problems arise when applying gcd(a,b) with a mod p or b mod p :/
Well, it seems the judge where this problem is was shut down. Hope they fix the problem soon :(