| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
Given n numbers a[1] to a[n], 2 player play a game alternately as follows. In the beginning of game, we have a number g = 0. They chose one of the numbers in the array a which is not thrown out and replace g by gcd(g, a[i]). After that they throw a[i]. If at any time in the game g becomes 1, the person who made the value g of equal to 1 loses. If a person is not able to move, then also he loses.
There are two questions to answer. 1. Who will win if they play optimally. 2. What is probability of winning of first player if they play randomly.
I'd like to share my solution to part 2 which is different from the editorial.
Any game they play is a permutation of a (let them play all n numbers, even someone already lose). Let's call this permutation b. Since they play uniformly randomly, the permutation is also chosen uniformly randomly from all n! permutations.
Let 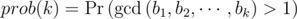 for 1 ≤ k ≤ n.
for 1 ≤ k ≤ n.
If the game ends exactly on the k th turn, that means  , but
, but  . Therefore the probability is prob(k - 1) - prob(k). If prob(n + 1) is defined as 0, then k = n + 1 is also applied. Sereja wins if and only if the game ends on even number turns, so the answer is (prob(1) - prob(2)) + (prob(3) - prob(4)) + ....
. Therefore the probability is prob(k - 1) - prob(k). If prob(n + 1) is defined as 0, then k = n + 1 is also applied. Sereja wins if and only if the game ends on even number turns, so the answer is (prob(1) - prob(2)) + (prob(3) - prob(4)) + ....
All that's left is calculate prob(k). Let 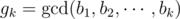 , we can calculate separately the probability that gk is a multiple of p, where p is a prime, and add them up. By the inclusion-exclusion principle, we also have to subtract the probability that gk is a multiple of p1 p2, where p1 and p2 are primes, and add back the probability that gk is a multiple of p1 p2 p3, where p1, p2 and p3 are primes. Fortunately, there is no number under 100 having 4 different prime factors.
, we can calculate separately the probability that gk is a multiple of p, where p is a prime, and add them up. By the inclusion-exclusion principle, we also have to subtract the probability that gk is a multiple of p1 p2, where p1 and p2 are primes, and add back the probability that gk is a multiple of p1 p2 p3, where p1, p2 and p3 are primes. Fortunately, there is no number under 100 having 4 different prime factors.
Finally, let's calculate the probability that gk is a multiple of m. Say there are c numbers in a that are multiples of m. Note that b1, b2, ..., bk must all be multiples of m, so all chosen from these c numbers. The number of combinations is 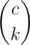 and the number of permutations is
and the number of permutations is  . So the probability is
. So the probability is 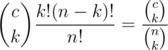 .
.
My solution: http://www.codechef.com/viewsolution/3906540
Manasa and Combinatorics is one of the problems in Ad Infinitum April'14. The problems are very interesting, and some mathematical insights are required. Thanks to Shashank Sharma for organizing the great competition.
Here is the upcoming Ad Infinitum May'14.
Someone sent me a message asking how I got the formula in this problem, so I figured why not post it somewhere for everyone to see.
The problem asks the number of strings consisting of N number of A's and 2N number of B's, without any prefix or suffix having more A's than B's.
The editorial can be found here, and as you can see in this pdf file, the formula in the code can be derived algebraically.
Here, I would like to provide another point of view, that is easier to visualize. (The following images are from here.)
Forgetting the constraint about prefixes and suffixes. What's the number of strings with N number of A's and M number of B's? The problem is equivalent to asking the number of different paths from P(0, 0) to Q(M, N), if you consider A as going up and B as going right. In the images M = 5 and N = 3. The answer is 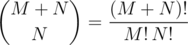 .
.

Now if we want every prefix to have no more A's than B's. The corresponding paths must not cross the green line (y = x), and hence not intersecting the red line (y = x + 1).

However, if a path intersecting the red line, the part before intersecting can always be reflected with respect to the red line, and be mapped to a path from P′( - 1, 1) to Q(M, N). Subtracting the number of paths intersecting the red line, we get that the number of strings with wrong prefixes is 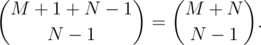

What about suffixes? You can rotate the grid 180 degrees and imagine another red line at the bottom right corner, and the original Q(M, N) is reflected similarly to Q′(M + 1, N - 1). Every path touching the bottom-right red line is mapped to unique path from P to Q′, so the number is again 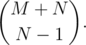

Finally, because of the inclusion-exclusion principle, we have to find the strings that have both wrong prefixes and suffixes. That's exactly the number of paths from P′( - 1, 1) to Q′(M + 1, N - 1)! Therefore, the formula is 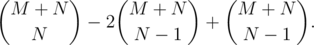
All that's left is calculate 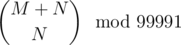 for M, N ≤ 1012. You can use Lucas' theorem. Since I didn't know the theorem before reading the editorial, I used this formula to calculate a and e where N! = a × 99991e.
for M, N ≤ 1012. You can use Lucas' theorem. Since I didn't know the theorem before reading the editorial, I used this formula to calculate a and e where N! = a × 99991e.
P.S. I also like the problem Ichigo and Cube very much.
Many thanks to brunoja. He is the main contributor now. Please try it out and give us feedback. You're also welcome to fork the project or join us as a collaborator.
https://github.com/johnathan79717/codeforces-parser
Codeforces Parser v1.4.1
Summary
Codeforces is a website for competitive programming. It holds contests, so-called Codeforces Rounds, about every week.
This is a python program that parses the sample tests from the contest problem pages. For each problem, it generates the sample input/output files and a shell script to run sample tests.
You can also find this article here, http://codeforces.me/blog/entry/10416
Example:
./parse.py contest_number (e.g. ./parse.py 464)
Where 464 is the contest number, not the round number! Check the URL of the contest on your browser, that is the number you are supposed to use.
Effect:
What will happen, for example, if ./parse.py 464 is executed?
- Directories
464/A,464/B,464/C,464/Dand so on are created depending on the contest number of problems. - For each problem,
main.ccis copied and renamed to the problem letter to the corresponding directory. You can put the path of your usual template inparse.py:20. - Problem page is downloaded from Codeforces website, and parsed. Sample input/output files are generated, e.g.
input1,output1,input2,output2and so on. You can create your own test cases after that, just keep the same naming format as others test cases. - A script
test.shis generated. You can use it to compile and run the sample tests after you finish coding. Just run./test.shin the problem directory.
What will happen if ./test.sh is executed?
- Compilation:
g++ -g -std=c++0x -Wall main.cc. You can change the compile options inparse.py:21. - Run each sample tests on your program (
a.out), and check the output bydiff. If it's correct, print Accepted, or else print the sample test that went wrong.
Collaborators and Versions:
List of CodeForces Collaborators:
If you have any suggestions and/or bugs drop a message!
Versions Changes:
- 1.4.1: Minor fixes, such as typos, bugs and special characters handling.
- 1.4: Changed how the parser gets the problems. During the competitions the page is slightly different. Fixed some invalid character on input and output causing the script to crash. Forcing a new line on the input/output if there is none. Fixed some line number information in this README file.
- 1.3: Some minor fixes and code organizing. Also fixed some typos. Removed the sample from default input and output files.
- 1.2: Fixed some typos and constants. Fetching contest info, printing contest name and problem names. The contest may now have more or less than 5 problems, it will auto detect. The script will now generate the template with the problem letter. Fixed test cases fetching. The script was stopping for escaped html characters, such as '<'. Fixed script to work with python 3.
- 1.1: Cleaner generation of the test script, now it auto detects the test cases, making you able to create your own cases. Echo color output, for accepted we get a green message, otherwise it is red. Added the time measurement for running the test cases. For the runtime error case, it now outputs the input case. Created some constants, such as compile options. These user modifiable constants should be easily spotted at the first lines of the python script.
- 1.0: Initial Version.
Todo, Bugs & Troubleshootings:
- In OS X it is necessary to install the
gnu-timeto measure time. - This parser currently works only on Unix OSes. If you want to add Windows/Other support let us know.
Can anyone please explain to me the answer of #124 (Div. 2) problem A?
http://www.codeforces.com/problemset/problem/197/A
I've seen other contestants' code.
It seems that if the First player wins if he can put his first plate on the table.
But I still can't figure out why.
Is the reason simple so that many people solved that during the contest, or they just guessed it?
| Name |
|---|










