Всем привет!
Написал тут пост "Зачем делать Ph. D. по Computer Science" по свежим следам. Прочитайте сами и перешлите, пожалуйста, эту ссылку своим знакомым студентам-математикам/программистам!
Илья
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
Всем привет!
Написал тут пост "Зачем делать Ph. D. по Computer Science" по свежим следам. Прочитайте сами и перешлите, пожалуйста, эту ссылку своим знакомым студентам-математикам/программистам!
Илья
Hi all,
Can you help me test our implementation of the Fast Hadamard Transform? It will take you a couple of minutes provided that you have modern enough C and C++ compilers. I'm especially interested in testing it under OS X and 32-bit systems.
You would need to have gcc that would compile C99 and g++ that would compile C++11. Also, you would need make to build everything.
What you need to do:
Thanks! Ilya
Hi all,
I'm about to teach AVL trees for a section of 6.006, and while thinking it through, I came up with the following question, which, I strongly suspect, should be well-understood.
Say one wants to maintain a binary search tree with height 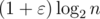 , where n is the total number of nodes, under insertions. How quickly can one insert? Is time
, where n is the total number of nodes, under insertions. How quickly can one insert? Is time 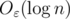 per insert possible?
per insert possible?
For instance, AVL trees achieve height around 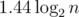 and red-black trees —
and red-black trees — 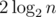 .
.
What do you think?
Подумал, что может кому-то будет интересно.
В этом видео моего доклада на факультете компьютерных наук ВШЭ я сначала рассказываю, как искать ближайших соседей в высокой размерности с помощью Locality-Sensitive Hashing, а потом рассказываю про наше недавнее улучшение (2015 года), которое позволяет этот самый поиск существенно ускорить (в теории).
Hi everyone!
We have just started a student blog of MIT Theory of Computation Group. If you are curious to read or gossip about "real" research in Theoretical Computer Science or life of graduate students, feel free to sign up!
The blog is run by:
Дан выпуклый четырехугольник со сторонами a, b, c, d (a >= b >= c >= d, стороны могут идти в любом порядке). Доказать, что a + b + d не меньше суммы длин диагоналей.
Всем привет!
Мы с ilyakor написали минималистичный клон PasswordMaker. Вкратце идея: вместо того, чтобы помнить N разных паролей, помним один (master password), а затем, чтобы, к примеру, получить пароль для gmail.com, мы просто вычисляем H(master-password || gmail.com), где H -- криптографическая хеш-функция (мы используем SHA-512).
Это был наш первый опыт написания кода для Android, с основной логикой и интерфейсом мы худо-бедно справились (вот ссылка на github), но с дизайном полная беда. Пока это выглядит примерно так:
Может быть, найдется доброволец, который перерисует все четыре layout'а, чтобы это не выглядело настолько тошнотворно? По нашим прикидкам, у человека с более-менее прямыми руками это должно занять минимальное время (поправьте нас, если это не так!).
Судя по тренировкам, наша команда не прошла бы на NEERC от МГУ, но пройдя четвертьфинал в Providence (порядка 15 команд, мы решили 4 из 7 задач) и полуфинал в Rochester'е (порядка 10 команд, 6 из 8 задач), мы оказались в финале ACM ICPC. Теперь мы поедем в Санкт-Петербург представлять MIT.
Состав: Рати Гелашвили (kerensky), Sepideh MahAbadi, Илья Разенштейн (ilyaraz).
AlexanderBolshakov недавно привел ссылку на замечательную задачу: номер 4 отсюда. Прекрасная задача, всех призываю над ней подумать и, если придумаете, запрограммировать. Давайте, чтобы было чуть-чуть понятнее, что происходит, я попробую погрузить ее в некоторый контекст.
Есть идеи?
Пусть у нас есть связный неориентированный граф без петель и кратных ребер, в котором n вершин и m ребер. Докажите, что в нем найдется C·n2 / m вершин, которые попарно не соединены ребрами, где C — какая-то абсолютная константа.
Очередная задача по теории вероятностей.
Рассмотрим единичную сферу в n-мерном пространстве: 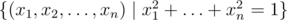 . Выберем на ней точку (x1, x2, ..., xn) равномерно. Какое (с точностью до мультипликативной константы) математическое ожидание случайной величины
. Выберем на ней точку (x1, x2, ..., xn) равномерно. Какое (с точностью до мультипликативной константы) математическое ожидание случайной величины 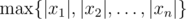 ?
?
Ответы (если, конечно, таковые будут) просьба аргументировать.
Рассмотрим игру для двух игроков. Первый загадывает два числа от 1 до n. Второй пытается получить об этой паре максимальную информацию. Для этого он называется подмножества {1, 2, ..., n}, а первый сообщает про какое-то из своих чисел, лежит ли оно в этом множестве. Что скрывается под словосочетанием "максимальная информация", и за какое асимптотически минимальное количество вопросов ее можно узнать?
Пусть у нас есть множество A, которое состоит из m целых чисел от 1 до n (будем считать, что 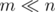 , например, что m = no(1)). Мы хотим построить структуру данных, которая по числу будет определять, лежит ли оно в A. При этом, у нас будет жесткое ограничение: на каждый запрос алгоритм должен смотреть лишь на один бит структуры.
, например, что m = no(1)). Мы хотим построить структуру данных, которая по числу будет определять, лежит ли оно в A. При этом, у нас будет жесткое ограничение: на каждый запрос алгоритм должен смотреть лишь на один бит структуры.
Какого минимального размера структуры можно достичь:
если алгоритм должен всегда выдавать верный ответ,
если алгоритм может ошибаться с вероятностью 1 процент (но при этом должен выдавать верный ответ с вероятностью 99 процентов для любого запроса)?
Рассмотрим евклидову версию задачи TSP: на плоскости есть n точек, нужно построить цикл минимальной длины, который проходит через все точки ровно по одному разу.
Все олимпиадники делятся на два лагеря: те, кто отлаживает в отладчике, и те, кто отлаживает отладочным выводом. Можно бесконечно спорить о том, какой метод удобнее, но факт остается фактом -- и таких, и таких людей полным-полно. Я отношусь ко второму лагерю: во многих ситуациях применение отладчика невозможно, поэтому хочется быть от него независимым. Более того, лично для меня отладочный вывод удобнее (я использую отладчик только для того, чтобы понять, где именно программа упала).
Обнаружил сегодня забавный момент в Python'е.
Представьте себе, что у вас есть список списков x. Например, x = [[1, 2, 3], [], [[6, 6, 6]]]. Мы хотим сконкатенировать все элементы x и получить в данном случае [1, 2, 3, [6, 6, 6]]. Наука это учит делать красиво: sum(x, []). Действительно, сложение для списков -- это просто-напросто конкатенация.
Однако, у данного подхода есть существенный недостаток. Если, к примеру, у нас k списков константной длины, то sum(x, []) будет работать за время O(k2), а не O(k), как разумеется хотелось бы. Это происходит вот почему: результат сложения списков записывается в новое место, и на выделение памяти каждый раз уходит линейное время. Проблема. Однако, простой цикл спасает положение.
result = []
for element in x: <перенос строки + таб> for item in element: <перенос строки + таб + таб> result.append(item)
Действительно, append работает за учетное время O(1).
Внимание, бонусный вопрос: как сделать конкатенацию всех элементов за время O(k) в "функциональном" стиле?
В комментариях к предыдущему посту Alex_KPR и mastersobg интересовались, как выглядит система Stackoverflow. Попробую вкратце это объяснить (но, конечно, рекомендуется RTFM).
Все состоит из вопросов и ответов. На каждый вопрос может в каждый момент быть от нуля до бесконечности ответов. К вопросам и ответам можно оставлять комментарии.
У каждого участника есть целое число -- репутация. Изначально она равна нулю. Чтобы задавать вопросы и отвечать на них сгодится любая репутация. Вопросы и ответы можно плюсовать и минусовать. Плюс означает +10 репутации спросившему или ответившему. Минус означает -2 репутации спросившему или ответившему и -1 репутации минусующему. Ответы к вопросу показываются отсортированными по сумме плюсов и минусов. Вопросы, соответственно, тоже можно фильтровать.
Можно зарабатывать не более 200 репутации в день.
Вопросы и ответы бывают обычные и community wiki. Вопросы и ответы community wiki тоже можно плюсовать и минусовать, но на репутацию спросившего или ответившего это никак не влияет. Ответы к посту community wiki автоматически являются community wiki. Вопрос становится community wiki в следующих случаях: вопрос отредактировали 4 человека, автор вопроса отредактировал его 8 раз, автор явно указал, что вопрос community wiki, на вопрос более 30 ответов. Статус community wiki отменить нельзя.
Репутация дает некоторые права.
10 задавать community wiki вопросы
15 плюсовать
15 помечать специальным флагои спам
15 постить более одной ссылки
15 постить изображения
50 оставлять комментарии
100 минусовать
100 редактировать community wiki вопросы и ответы
100 задавать более одного вопроса в 20 минут
100 оставлять более одного ответа в 2 минуты
100 предлагать часть своей репутации за хороший ответ на вопрос
250 голосовать за закрытие или переоткрытие своих вопросов
250 создавать новые тэги
500 изменять тэги вопросов
2000 редактировать любые вопросы и ответы
3000 голосовать за закрытие или переоткрытие любых вопросов
10000 удалять закрытые вопросы
10000 доступ к инструментам модератора (что бы это ни значило)
Если вам что-то непонятно, спрашивайте.
Недавно в Голландии прошел subj. Результатов я пока не видел, но русские условия уже есть. Перепечатаю их сюда. Если кому-нибудь интересно, можно обсудить задачи. :)
Интересно, есть ли на codeforces участники IMO 2011? А прошлых лет?
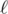 , на которой лежит ровно одна точка
, на которой лежит ровно одна точка 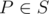 . Прямая
. Прямая 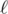 вращается по часовой стрелке вокруг центра P до тех пор, пока она впервые не пройдет через другую точку множества S. В этот момент эта точка, обозначим ее Q, становится новым центром, и прямая продолжает вращаться по часовой стрелке вокруг точки Q до тех пор, пока она снова не пройдет через точку множества S. Этот процесс продолжается бесконечно. Докажите, что можно выбрать некоторую точку
вращается по часовой стрелке вокруг центра P до тех пор, пока она впервые не пройдет через другую точку множества S. В этот момент эта точка, обозначим ее Q, становится новым центром, и прямая продолжает вращаться по часовой стрелке вокруг точки Q до тех пор, пока она снова не пройдет через точку множества S. Этот процесс продолжается бесконечно. Докажите, что можно выбрать некоторую точку 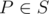 и некоторую прямую
и некоторую прямую 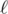 , проходящую через P, так, что для мельницы, начинающейся с
, проходящую через P, так, что для мельницы, начинающейся с 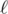 , каждая точка множества выступит в роли центра бесконечное число раз.
, каждая точка множества выступит в роли центра бесконечное число раз.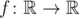 - функция, определенная на множестве действительных чисел и принимающая действительные значения, такая, что f(x + y) ≤ yf(x) + f(f(x)) для всех действительных x и y. Докажите, что f(x) = 0 для всех x ≤ 0.
- функция, определенная на множестве действительных чисел и принимающая действительные значения, такая, что f(x + y) ≤ yf(x) + f(f(x)) для всех действительных x и y. Докажите, что f(x) = 0 для всех x ≤ 0.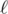 - некоторая касательная к окружности Γ, и пусть
- некоторая касательная к окружности Γ, и пусть 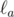 ,
, 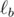 и
и 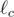 - прямые, симметричные прямой
- прямые, симметричные прямой 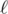 относительно прямых BC, CA и AB соответственно. Докажите, что окружность, описанная около треугольника, образованного прямыми
относительно прямых BC, CA и AB соответственно. Докажите, что окружность, описанная около треугольника, образованного прямыми 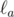 ,
, 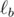 и
и 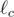 , касается окружности Γ.
, касается окружности Γ.Если вы хотите, чтобы operator[] (а не только at()) у класса std::vector выполнял проверку на выход за пределы массива, то нужно дописать следующую строчку перед инклюдами (речь идет о g++).
#define _GLIBCXX_DEBUG
Тогда при попытке выйти за пределы массива выдается примерно такое сообщение:
/usr/include/c++/4.4/debug/vector:265:error: attempt to subscript container
with out-of-bounds index 1, but container only holds 1 elements.
Objects involved in the operation:
sequence "this" @ 0x0x7fffe4f2e9f0 {
type = NSt7__debug6vectorIiSaIiEEE;
}
Aborted
По-моему, для олимпиад очень полезная вещь. Java и пр. отдыхают! :)
UPD
Другой способ решения данной проблемы: написать в начале файла что-то типа http://pastebin.com/6HDaceHq . Тогда operator[] просто заменится на at(). Это решение более хорошее по двум причинам:
Вот две задачи по терверу, которые сами по себе довольно простые и не неожиданные, но в них на мой вкус очень забавные ответы. Итак...
1. Представьте себе, что мы хотим сгенерировать случайный бит следующим странным способом. Возьмем очень-очень большое натуральное n и случайный двудольный граф, в каждой доле которого по n вершин. Посчитаем в нем количество совершенных паросочетаний (наборов из n ребер, которые не имеют общих концов). Четность этого количества и будет нашим битом. Какова вероятность, что этот бит будет равен нулю?
2. Представьте себе, что у нас есть n корзинок, в которые мы случайно бросаем шары. Мы продолжаем процесс, пока в каждой корзинке не будет по крайней мере m шаров. Сколько в среднем шаров мы бросим? Интересует ответ с точностью до константы. Например, хорошо известно, что если m = 1, то в среднем мы бросим 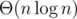 шаров.
шаров.
Раз уж всплыл мой пост годовой давности, то позволю себе запостить еще одну несложную, но, на мой вкус, очень красивую задачу. Если вы знали ее решение раньше, то не пишите его пожалуйста (можете написать фразу типа "я уже знал решение").
Задача: прямоугольник разбит на несколько прямоугольников так, что у каждой части есть по крайней мере одна сторона с целой длиной. Доказать, что и у исходного прямоугольника хотя бы одна целая сторона.
Хотелось бы написать про хак, который может помочь ускорить двоичный поиск на очень больших массивах.
Дело в том, что обычный двоичный поиск весьма неэффективен с точки зрения кэша: вначале, пока границы поиска далеко друг от друга, запросы к массиву будут далеки друг от друга, что породит много кэш-промахов.
Как с этим бороться? Очень просто. Пусть n -- размер массива. Разобьем массив на  блоков длины
блоков длины  . Образуем массив B из первых элементов блоков. Теперь, чтобы сделать двоичный поиск в исходном массиве, достаточно сначала поискать элемент в B, а потом в соответствующем отрезке длины
. Образуем массив B из первых элементов блоков. Теперь, чтобы сделать двоичный поиск в исходном массиве, достаточно сначала поискать элемент в B, а потом в соответствующем отрезке длины  в исходном массиве. Таким образом, количество промахов существенно уменьшится.
в исходном массиве. Таким образом, количество промахов существенно уменьшится.
Абсолютно аналогичная конструкция возможна для любого числа уровней.
Для эксперимента я сравнил std::lower_bound и оптимизированную версию двоичного поиска (трехуровневую) на случайном массиве 32-битных целых чисел размера 227. Количество запросов равно 107. Машинка: Intel(R) Core(TM) i5 CPU M 430 @ 2.27GHz, 32k/256k/4m cache, 1066 MHz RAM. Система: GNU/Linux 2.6.35, g++ 4.4.5.
Результат:
| Название |
|---|


