The closest pair of points problem is a well-known problem in computational geometry (it is also in SPOJ) and several efficient algorithm to solve it exists (divide and conquer, line sweep, randomization, etc.) However, I thought it's a bit tedious to implement them, and decided to solve it naïvely.
The naïve algorithm is as follows: first, sort the points along the x axis, then, for each pair of points whose difference in the x coordinate is less than the optimal difference so far, compute the distance between the points. This somewhat heuristic algorithm fails when all of the x coordinates of the points are the same, so the running time is O(n2).
What I did to get an AC at SPOJ is pick up a random angle θ and rotate the points around the origin by θ at the beginning of the algorithm. This (I hope) makes the heuristic work and I got an AC.
The problem is the complexity of this randomized algorithm. Some say its average running time is 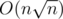 . How do you prove this?
. How do you prove this?









 , and thus this works even if
, and thus this works even if  time.
time. :
:  , iff
, iff  s.t.
s.t. 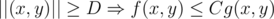 .
.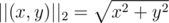 (Euclidean)
(Euclidean)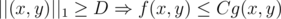 . The set of points
. The set of points 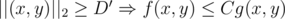 , and this means
, and this means 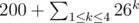 . A
. A 
