ikk's blog

Multivariable asymptotics
By ikk, 13 years ago, In English

The following fact may be elementary and obvious to some people, but I'd been confused regarding this topic for some time, so I wrote this blog post.

The definition of the big O notation is usually given for one-variable functions in introductory textbooks, so when I talked or read about graph algorithms, I used notations like O(|V| + |E|) without really understanding their meaning.

Adapting the definition for one-variable functions, I get this definition for multi-variable functions, say, :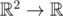

, iff s.t. .
The question is what norm we are talking about.  Here are some norms we're used to:
  • ||(x, y)||1 = |x| + |y| (Manhattan)
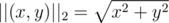  • (Euclidean)
  • ||(x, y)||∞ = max \{|x|, |y|\} (Infinity)

Of course, unless otherwise stated, norm means the Euclidean norm. But the other two norms seems simpler: in computer science x and y are in most cases integers, so why do you have to bother with irrational numbers?

As it turns out, the three norms above are equivalent in terms of defining the meaning of O(g). Suppose 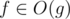in terms of the Manhattan norm, i.e., 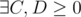s.t. 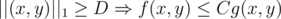.  The set of points {(x, y): ||(x, y)||1 ≥ D} is the region outside a square enclosing the origin, and if we replace the norm with the Euclidean norm, it becomes the region outside a circle.  So if we take D′ so that the circle {(x, y): ||(x, y)||2 = D′} encloses the square {(x, y): ||(x, y)||1 = D}, we have 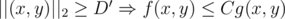, and this means 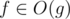in terms of the Euclidean norm, too.  The rest of the proof goes similarly.

EDIT: I've just read that all norms of a finite-dimensional vector space induce the same topology in a textbook.  I'd like to know if this is relevant to what I've written.

  • Vote: I like it
  • +32
  • Vote: I do not like it

13 years ago, # |
  Vote: I like it 0 Vote: I do not like it
As D just denotes the maximum value, for which we still allow f(x, y) to be larger than Cg(x, y), I think the purpose of the norm is simply to evaluate the quantity of (x, y) in some way. So in this case any symmetrical (in relation to x and y) norm will do the job.
→ Reply
  • 13 years ago, # ^ |
    ← Rev. 7   Vote: I like it +10 Vote: I do not like it

    I suspect that in fact any norm will do.  An "asymmetrical" norm like ||(x, y)||? = max{|x|, 2|y|} gives the same definition of O (you can tell this by replacing 'square' with 'rectangle' in the argument above).

    EDIT: By the way, an asymmetrical norm seems to mean a generalization of a norm in which ||v|| is not necessarily equal to || - v||.

    → Reply
    • 13 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it
      Seems so. Similar to your argument, if we have some norm, than we can both inscribe and exscribe to it some symmetrical norm (say, circle). That means that if the definition works for a circle, then it works for this norm, also (if a circle is inscribed). And contrary: if the definition works for this norm, it works also for a circle (if a circle is excribed). So we have established a bijection of both definitions.
      → Reply
      • 13 years ago, # ^ |
          Vote: I like it +2 Vote: I do not like it
        Note that this doesn't work for some half-norms like min(|x|,|y|) which can be very useful in practice.
        → Reply
        • 13 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it
          What are half-norms?
          → Reply
          • 13 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it
            Norm that can be zero on non-zero elements.
            → Reply
          • 13 years ago, # ^ |
            ← Rev. 2   Vote: I like it +8 Vote: I do not like it

            There is one difference between norms and semi-norms: a semi norm is allowed to assign 0 to some vectors that are not 0.

            By the way, min(|x|, |y|) is not a semi-norm, because it doesn't satisfy the triangular inequality; take the two vectors (0, 1) and (1, 0) for a counter-example.

            → Reply
    • 13 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      I agree, any norm will do, since all norms are equivalent in a finite dimension space.  See the properties of a norm.
      If it's a norm, || - v|| should be equal to ||v||, according to the first property.
      → Reply
      • 13 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        Well, I mentioned asymmetrical norms because in the first version of the post I used the word "asymmetrical norm" without knowing that's a technical term that refers to diffrent things than I described.  (The relative pronoun "which" refers to "a generalization".)

        → Reply
        • 13 years ago, # ^ |
          ← Rev. 2   Vote: I like it +8 Vote: I do not like it

          All asymmetrical norms are also equivalent in a finite dimension space.

          Moreover, all continuous functions f: R^n -> R are equivalent if f(a*x) = a*f(x), for any positive a.

          → Reply
          • 13 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it
            That's amazing.  The proof below almost applies to asymmetrical norms, but it uses the triangule inequality, so how do you prove it for such continuous mappings in general?
            → Reply
            • 13 years ago, # ^ |
                Vote: I like it +3 Vote: I do not like it
              In the proof, the triangular inequality is needed to prove the continuity of the norm.  To adapt to the case of a continuous function f such that f(a * x) = a * f(x), for any positive a,  this part of the proof is not needed anymore.
              → Reply
              • 13 years ago, # ^ |
                ← Rev. 2   Vote: I like it 0 Vote: I do not like it

                Ah yes, thanks.  (I read the proof, forgot it, read anonymous' post, skimmed the proof again, found the triangle inequality
                and thought "oh this doesn't apply to continuous mappings in general".  I should be more careful.)

                → Reply
            • 13 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it


              → Reply
        • 13 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Thanks for the clarification.  It looks confusing that "asymmetric norm" is more general than " norm".  Oh well.

          → Reply
      • 13 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it
        Here's the link to the proof
        → Reply