So my O level Chinese exam is in 2 days so I decided to learn a data structure that I can only find resources for in Chinese. I thought I might as well write a tutorial in English.
This data structure is called 析合树, directly translated is cut join tree, but I think permutation tree is a better name. Honestly, after learning about it, it seems like a very niche data structure with very limited uses, but anyways here is the tutorial on it.
Thanks to dantoh and oolimry for helping me proofread.
Motivation
Consider this problem. We are given a permutation,$$$P$$$ of length $$$n$$$. A good range is a contiguous subsequence such that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$. This can be thought of the number of contiguous subsequence such that when we sort the numbers in this subsequence, we get contiguous values. Count the number of good ranges.
Example: $$$P=\{5,3,4,1,2\}$$$.
All good ranges are $$$[1,1], [2,2], [3,3], [4,4], [5,5], [2,3], [4,5], [1,3], [2,5], [1,5]$$$.
The $$$O(n^2)$$$ solution for this is using sparse table and checking every subsequence if it fits the given conditions. But it turns out we can speed this up using permutation tree to $$$O(n\log{n})$$$.
Definitions
A permutation $$$P$$$ of length $$$n$$$ is defined as:
- $$$|P|=n$$$
- $$$\forall i, P_i \in [1,n]$$$
- $$$\nexists i,j \in [1,n], P_i \ne P_j$$$
A good range is defined as a range, $$$[l,r]$$$ such that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$ or equivalently $$$\nexists x,z \in [l,r], y \notin [l,r], P_x<P_y<P_z$$$.
We denote a good range $$$[l,r]$$$ of $$$P$$$ as $$$(P, [l,r])$$$, and also denote the set of all good ranges as $$$I_g$$$.
Permutation Tree
So we want a structure that can store all good ranges efficiently.
Firstly, we can notice something about these good ranges. They are composed by the concatenation of other good ranges.
So the structure of the tree is that a node can have some children and the range of the parent is made up of the concatenation of the children's ranges.
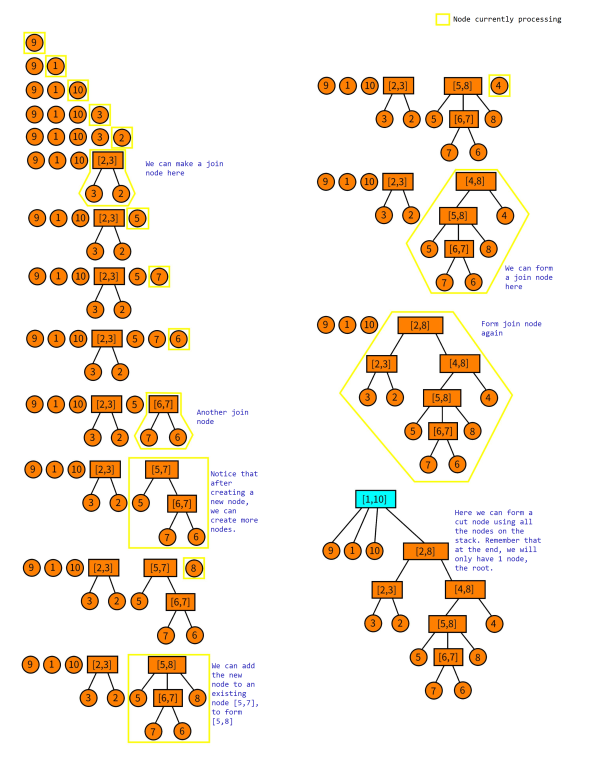
Here is an example permutation. $$$P=\{9,1,10,3,2,5,7,6,8,4\}$$$.

As we can see from the above image, every node represents a certain good range, where the values in the node represent the minimum and maximum values contains in this range.
Notice in this data structure, for any 2 nodes $$$[l_1,r_1]$$$ and $$$[l_2,r_2]$$$, WLOG $$$l_1 \leq l_2$$$, either $$$r_1<l_2$$$ or $$$r_2 \leq r_1$$$.
Definition of Cut Nodes and Join Nodes
We shall define some terms used in this data structure:
- Node range: For some node $$$u$$$, $$$[u_l,u_r]$$$ will describe the minimum and maximum value contained in the range the node represents
- Ranges of children: For some non-leaf node $$$u$$$, let the array $$$S_u$$$ denote the array of the ranges of its children. For example, the root node the above picture, $$$S_u$$$ is $$$\{[9,9],[1,1],[10,10],[2,8]\}$$$.
- Order of children: For some non-leaf node $$$u$$$, we can discretize the ranges in $$$S_u$$$. Again using the example of the root node, the order of its children is $$$\{3,1,4,2\}$$$, we will call this $$$D_u$$$.
- Join node: For some non-leaf node $$$u$$$, we call it a join node if $$$D_u=\{1,2,3,\cdots\}$$$ or $$$D_u=\{\cdots,3,2,1\}$$$. For simplicity we also consider all leaf nodes to be join nodes.
- Cut node: Any node that is not a join node.
Properties of Cut Nodes and Join Nodes
Firstly, we have this very trivial property. The union of all ranges of children is the node's range. Or in fancy math notation, $$$\bigcup_{i=1}^{|S_u|} S_u[i]=[u_l,u_r]$$$.
For a join node $$$u$$$, any contiguous subsequence of ranges of its children is a good range. Or, $$$\forall i,j,1 \leq i \leq j \leq |S_u|, \bigcup_{i=l}^{r} S_u[i]\in I_g$$$.
For a cut node $$$u$$$, the opposite is true. Any contiguous subsequence of ranges of its children larger than 1 is not a good range. Or, $$$\forall i,j,1 \leq i < j \leq |S_u|, \bigcup_{i=l}^{r} S_u[i]\notin I_g$$$.
The property of join nodes is not too hard to show by looking at the definition of what a join node is.
But the property of cut nodes is slightly harder to prove. A way to think about this is that for some cut node such that there is a subsequence of ranges bigger than 1 that form a good range, then that subsequence would have formed a range. This is a contradiction.
Construction of Permutation Tree
Now we will discuss a method to create the Permutation Tree in $$$O(n\log{n})$$$. According to a comment by CommonAnts, the creator of this data structure, a $$$O(n)$$$ algorithm exists, but I could not find any resources on it.
Brief overview of algorithm
We process the permutation from left to right. We will also keep a stack of cut and join nodes that we have processed previously. Now let us consider adding $$$P_i$$$ to this stack. We firstly make a new node $$$[P_i,P_i]$$$ and call it the node we are currently processing.
- Check if we can add the currently processed as a child of the node on top of the stack.
- If we cannot, check if we can make a new parent node (this can either be a cut or join node) such that it contains some suffix of the stack and the current processed node as children.
- Repeat this process until we cannot do any more operations of type 1 or 2.
- Finally, push the currently processed node to the stack.
Notice that after processing all nodes, we will only have 1 node left on the stack, which is the root node.
Details of the algorithm
For operation 1, if we note that we can only do this if the node on top of the stack is a join node. Because if we can add this as a child to a cut node, then it contradicts the fact that no contiguous subsequence of ranges of children larger than 1 of a cut node can be a good range.
For operation 2, we need a fast way to find if there exists a good range such that we can make a new node from. There are 3 cases:
- We cannot make a new node.
- We can make a new join node. This new node has 2 children.
- We can make a new cut node.
Checking if there exists a good range
We have established for a good range $$$(P,[l,r])$$$ that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$.
Since $$$P$$$ is a permutation, we also have $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i \geq r-l$$$ for all ranges $$$[l,r]$$$.
Equivalently, we have $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i - (r-l) \geq 0$$$, where we have equality only for good ranges.
Say that we are currently processing $$$P_i$$$. We define a value $$$Q$$$ for each range $$$[j,i], Q_j=\max\limits_{j \leq k \leq i} P_k - \min\limits_{j \leq k \leq i} P_k - (i-j),0< j \leq i$$$. Now we just need to check if there is some $$$Q_j=0$$$, where $$$j$$$ is not in the current node being processed.
Now we only need to know how to maintain this values of $$$Q_j$$$ quickly when we transition from $$$P_i$$$ to $$$P_{i+1}$$$. We can do this by updating the max and min values every time it changes. How can we do this?
Let's focus on updating the max values since updating the min values are similar. Let's consider when the max value will change. It changes every time $$$P_{i+1} > \max $$$. Let us maintain a stack of the values of $$$\max\limits_{j \leq k \leq i}P_k$$$, where we will store distinct values only. It can be seen that this stack is monotonically decreasing. When we add a new element to this stack, we will pop all elements in the stack which are smaller than it and update their maximum values using a segment tree range add update. This amortizes to $$$O(n)$$$ as each value is pushed into the stack once.
Do note to decrement all $$$Q_j$$$ by 1 since we are incrementing $$$i$$$ by 1.
Now that we can maintain all values of $$$Q_j$$$, we can simply check the minimum value of the range we are interested in using segment tree range minimum queries.
If we can make a new cut node, then we greedily try to make new cut node. We can do this by adding another node from our stack until our new cut node is valid.
Since the above may be confusing, here is a illustration of how the construction looks like.
Problems using Permutation Tree
Codeforces 526F – Pudding Monsters
CERC 17 Problem I – Instrinsic Interval
Codeforces 997E – Good Subsegments










