Сегодня состоится Московский четвертьфинал-2013. Интернет-тур пройдёт также на системе ejudge, но на серверах Открытого Кубка. Соответственно, участвовать могут все команды, которые получили логины Открытого Кубка. Старт Интернет-тура в 11-00.
Также на задачах Интернет-тура (и самого четвертьфинала) будет проведено несколько матчей нового экспериментального проекта — Кубка Сборных. В этом турнире участвуют сборные, состоящие из 5 команд. В каждом туре участвующие сборные разбиваются на пары, после чего оказавшиеся в одной паре сборные играют между собой матч по правилам "Матча Гигантов", прошедшего на ЧУ-2013. За выигрыш по сумме задач сборная получает 3 очка, за выигрыш по суммарному штрафному времени при равном числе задач — 2 очка, за проигрыш по суммарному штрафному времени при равном числе задач — одно очко, за проигрыш по задачам — 0 очков.
Вход в систему (напоминаем, что тур стартует в 11-00 по московскому времени).
Жеребьёвка Кубка Сборных, состав сборных и окончательная формула будут опубликованы позднее.











А нельзя было заранее, хотя бы за сутки объявить об интернет-туре? Ни на официальном сайте, ни на сайте Открытого Кубка, ни на Snarknews никакой информации накануне не было.
А где текущие результаты посмотреть?
Должны быть где-то здесь http://acm.msu.ru/wp/, но пока нет.
По-моему здесь
А можно будет потом написать виртуально?
Да.
А задача А как решалась?
Можно было просимулировать. Возьмем 3 вершины с максимальным значением. Если у них у всех значения одинаковые, вычтем из всех по единице, иначе — вычтем из максимального 2, а из второго максимального 1. Будем повторять пока можем, прибавляя каждый раз 1 к ответу. Главное было это каждый раз за О(1) делать.
Будет ли открыто дорешивание?
Как K решалась?
Сгенерируем последовательность два раза. За первый раз узнаем старшие 16 бит ответа. Для этого нужно 216 интов, это мало памяти. Просто храним сколько чисел с такими старшими битами и в конце прошлись и посчитали.
За второй раз числа делятся на те, которые точно идут в ответ, те которые точно не идут в ответ, и те у которых 16 бит совпали. С последними разбираемся так же, как считали первые 16 бит.
Мне одному показалось, что боян?
Мы делали не так. Будем генерировать последовательность и записывать ее в массив. Как только размер массива стал 1.5 миллиона, применяем nth_element, оставляя только k максимальных чисел, после чего опять дописываем числа к получившемуся массиву. Работает меньше секунды на макстесте.
Да, задача уже давалась на московском четвертьфинале 2004 года под буквой J, но с другим форматом входных и выходных данных. Один боян на контест — это же не много :)
Об этом я не знал. Зато есть вот такое. Или имеется ввиду, что там сильно больше всего проходит?
Ну на тимусе можно сдать кучу. Память же у кучи линейная, вот только время n log n.
Я автор этой задачки.
Странно, но честно говоря я не думал, что она может оказаться бояном(тем не менее, не смотря на это, судя по результатам для подавляющего большинства команд она все-таки не оказалась бояном), что ещё очень странно — это то, что никто из остальных составителей задач "боянистости" не заметил.
Изначально я предполагал под правильным решением именно то, что написал KADR, правда вовсе не обязательно делать буффер именно на 1.5 миллиона чисел, 2k чисел вполне достаточно(хотя с 1.5 миллионами, теоретическая константа будет меньше).
Интересный факт, что вызвать nth_element на массиве из 100000000 миллионов чисел у меня в среднем работает чуть медленнее, чем пройтись по последовательности так, как описал KADR. Думаю, что дело в работе с кэшом.
В последствии оказалось, что сделать так, чтобы именно такое решение требовалось от участников очень сложно, так как если потребовать, чтобы задача была решена за один проход по последовательности, нужно было бы откуда то читать эти числа, а чтение откуда угодно этих чисел слишком трудоемкая операция, чтобы отделить O(n) от O(nlogn) на остальные операции.
К моему великому сожалению, 95% команд решило задачку именно чем-то типа сортировкой подсчетом(хотя, например, две команды ветеранов, которые прорешивали контест предварительно пользовались другими идеями).
А где можно условия посмотреть?
А есть таблица после разморозки? Или она до весны замерзла?
У нас еще награждение идет, таблицу на онсайте не разморозили.
Как C решалась?
(наблюдение 0: p2 и α нужны только чтобы ответ компактно выводить)
Наблюдение 1: если на каком-то отрезке вероятность константна, то это просто частота на этом отрезке (если в сторону частоты сдвинуть не получается из-за монотонности, то выгодно смёрджить с предыдущим/следующим отрезком).
Наблюдение 2: если есть какое-то решение, и какой-то отрезок в нём можно подразбить, то его всегда выгодно подразбить.
Итого, делается за линейный проход со стеком. Ну или можно более интуитивно проинтерпретировать: заменяем 0 на вектор (1, 0), 1 — на вектор (1, 1), и последовательно идём вдоль этих векторов; получаем ломаную. Из наблюдений 1-2 понятно, что надо найти нижнюю огибающую к ней.
Почему именно нижняя огибающая даёт оптимум? Кажется, что из наблюдений 1 и 2 следует, что в оптимуме нельзя подразбить отрезок, и что в оптимуме на каждом отрезке постоянства вероятностью будет частота. А вот вдруг получилось два различных разбиения на отрезки постоянства, так что дальше разбить их нельзя, и везде на отрезках постоянства вероятность — это частота?
P.S. Я понимаю, что вроде интуитивно похоже на правду и уже пора засылать -- это вполне себе ответ на мой вопрос. Всё же хотелось бы "честный ответ".
В терминах геометрической интерпретации:
1 => решение — это какая-то ломаная, вершины которой — подмножество вершин исходной ломаной; монотонность => ломаная выпукла вниз. Осталось понять, почему точки под ломаной — не выгодны. Посмотрим на какую-нибудь точку под ломаной, посмотрим на отрезок AB над ней, заменим его на AX и XB; при этом что-то могло сломаться с монотонностью. Надо показать, что если выкинуть все отрезки после B с наклоном меньше XB (то же самое для A), то целевой функционал не увеличится (с учётом подразбиения AB). Вот тут заканчивается геометрия и начинается страница вычислений :( Хотя возможно есть и красивое геометрическое объяснение, надо спросить у авторов.
А где дорешать можно?
А как решалась G(интерактивка)? Я правильно понял, что когда количество слонов отрицательно в input'е, то я могу купить/продать меньше, чем abs(x) (где x — количество слонов в input'е)?
Какое условие было: У вас есть два типа действий: sell и buy. На каждой итерации аукцион меняет какое-то своё состояние и вам нужно в этом новом состоянии заработать как можно больше денег.
Понимание приходит после разбора семпла: 1 итерация: аукцион готов купить 10 слонов по 100, мы слонов купить никак не можем, прибыль 0.
2 итерация: аукцион готов продать 4 слона по 98 и купить 10 по 100. Тогда мы эти 4 покупаем, продаем по 100, прибыль 8.
3 итерация: аукцион готов продать 4 слона по 98 и купить 3 по 100. Тогда теперь только 3 покупаем, продаем по 100, прибыль 6.
4 итерация: аукцион готов продать 4 слона по 98, купить 3 по 100 и 2 по 99. Прибыль: 1*(99-98)+3*(100-98) = 7
5 итерация: аукцион готов продать 1 слона по 97, 4 слона по 98, а купить 3 по 100 и 2 по 99. Прибыль: 1*(99-97)+3*(100-98)+1*(99-98)=9
Окей, давайте теперь придумаем хотя бы какое-то решение.
Утверждается, что работает такая стратегия: давайте возьмём два вектора: предложений sell и buy, отсортируем по стоимости его элементы, а затем будем покупать самых дешевых слонов, продавать их за как можно дороже, постепенно так сходясь двумя указателями, то есть один идём с префикса sell, другой с суффикса buy, пока либо не кончатся слоны где-то, либо стоимость продажи станет <= стоимости покупки, то есть профита от сделки мы уже не получим.
И это работает за O(M * M * lg(M)), где M -- количество запросов, что очень много. Давайте соптимайзим.
У нас есть, по сути, две медленных операции:
1) Нам нужно как-то уметь поддерживать два посортированных по стоимости вектора.
2) Нам нужно как-то быстро проходить двумя указателями, чтобы получить прибыль.
Давайте научимся делать это быстро.
Понятно, что для первой операции мы можем использовать какое-нибудь дерево. Можно взять декартово, и тогда просто сплитать его, и вставлять на нужное место наш новый элемент, или уже изменять значение у старого, если такая цена уже в нём была. Я на контесте ленивое дерево отрезков написал, потому что писать проще, то есть мы создаем дерево отрезков на 10^9 (максимальная цена операции), а узлы его создаем только по мере необходимости.
В итоге, я умею первую операцию делать очень просто за O(lg(109)) -- просто изменяя значение в соответствующем узле дерева отрезков/дд.
Со второй чуть хитрее. Давай попробуем бинпоиском перебрать количество слонов, которые мы купим, и, соотвественно, продадим. Понятно, что до некого момента мы будем увеличивать свою прибыль, а когда у нас этот указатель начнет покупать слонов за стоимость >= цены продажи, то это уже невыгодно.
Сразу проверим, что это количество меньше либо равно чем минимальное количество слонов в векторах buy и sell, иначе не получится никак.
Ок, допустим мы зафиксировали это количество.
Понятно, что мы теперь хотим купить слонов подешевле, а продать их подороже, поэтому нам интересен некий префикс вектора sell и суффикс вектора buy.
У нас вектор это дерево, поэтому если мы будем поддерживать в каждом узле количество суммарное слонов ниже, мы можем за один спуск находить максимальную цену покупки слона, и минимальную стоимость продажи слона, чтобы их количество на префиксе и суффиксе было больше либо равно зафиксированного количества в бин. поиске.
Ну и тогда всё просто, мы смотрим, что минимальная стоимость продажи > максимальная стоимость покупки, иначе уменьшаем количество в бин. поиске. В итоге мы находим такое максимальное количество слонов, которые выгодно продать.
Ну и прибыль наша считается тривильно, мы считаем сумму на префиксе в дереве, сумму на суффиксе, чуть-чуть их изменяем, потому что на префиксе/суффиксе могло быть не ровно k слонов и выводим разницу.
В итоге, вторая операция у нас работает за O(lg(262) * lg(109)).
Как-то жутко в описании получилось, на контесте выглядело проще :)
Видимо, второе действие можно без бин. поиска сделать, просто одним спуском, но заходило и так.
у большинства лишний бинпоиск не прокатывал вместо спуска, правда, он обычно был по цене
А как делать спуском за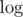 ? Мы подумали пару минут, получилось что-то относительно страшное, забили.
? Мы подумали пару минут, получилось что-то относительно страшное, забили.
Да всё тоже самое, спускаемся по цене, слева больше — идём вправо, справа больше — идём влево, на нижнем уровне добавляем объём или его часть по этой цене либо к праву либо к леву, в зависимости от того где больше, только при спуске пересчитываем не всё с нуля, а с учётом значений предыдущего шага
Я так понимаю, что дихотомия по объёму может проходить, поскольку начинаем не с 2^62, а с текущего минимума двух объёмов, он намного меньше, может просто теста не хватило с совсем небольшими ценами но очень жирными объёмами
Не понял. Нам требуется найти что-то страшное: такое максимальное k, что k-й элемент слева в одном дереве не больше, чем k элемент справа в другом дереве.
Может, есть пример кода?
как-то так Но здесь цифровой бор.
дерево можно сделать одно и считать в нём четыре параметра
Согласен, по сути это есть одно дерево:-) просто мне так понятнее было писать.
Спасибо! Очень подробно и понятно!)
Где есть результаты виртуального тура?
http://acm.math.spbu.ru:8087/~ejudge/res/joined
Где можно порешать виртуалку?
В координаторском интерфейсе OpenCup/ejudge есть ссылка на тренировки.Там ЧФ уже добавлен.
А вообще,
http://acm.math.spbu.ru:8087/~ejudge/team.cgi?contest_id=6570
Хм...у меня одного эта ссылка не грузится и не грузилась с сентября?
В Тренировках: 2013-2014 ACM-ICPC, NEERC, Московский четвертьфинал.