A: Exciting Bets
$$$GCD(a,b)=GCD(a-b,b)$$$ if $$$a>b$$$
$$$a-b$$$ does not change by applying any operation. However, $$$b$$$ can be changed arbitrarily.
If $$$a=b$$$, the fans can get an infinite amount of excitement, and we can achieve this by applying the first operation infinite times.
Otherwise, the maximum excitement the fans can get is $$$g=\lvert a-b\rvert$$$ and the minimum number of moves required to achieve it is $$$min(a\bmod g,g-a\bmod g)$$$.
Without loss of generality, assume $$$a>b$$$ otherwise we can swap $$$a$$$ and $$$b$$$. We know that $$$GCD(a,b) = GCD(a-b,b)$$$. Notice that no matter how many times we apply any operation, the value of $$$a-b$$$ does not change. We can arbitrarily change the value of $$$b$$$ to a multiple of $$$a-b$$$ by applying the operations. In this way, we can achieve a $$$GCD$$$ equal to $$$a-b$$$. Now, since $$$GCD(x,y)\leq min(x,y)$$$ for any positive $$$x$$$ and $$$y$$$, $$$GCD(a-b,b)$$$ can never exceed $$$a-b$$$. So, we cannot achieve a higher GCD by any means.
To achieve the required $$$GCD$$$, we need to make $$$b$$$ a multiple of $$$g=a-b$$$ using as few operations as possible. There are two ways to do so $$$-$$$ decrease $$$b$$$ to the largest multiple of $$$g$$$ less than or equal to $$$b$$$ or increase $$$b$$$ to the smallest multiple of $$$g$$$ greater than $$$b$$$. The number of operations required to do so are $$$b\bmod g$$$ and $$$g-b\bmod g$$$ respectively. We will obviously choose the minimum of the two. Also notice that $$$a\bmod g=b\bmod g$$$ since $$$a=b+g$$$. So, it doesn't matter if we use either $$$a$$$ or $$$b$$$ to determine the minimum number of operations.
$$$\mathcal{O}(1)$$$ per test case.
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
long long a,b;
cin >> a >> b;
if(a==b)
cout << 0 << " " << 0 << '\n';
else
{
long long g = abs(a-b);
long long m = min(a%g,g-a%g);
cout << g << " " << m << '\n';
}
}
}
B: Customising the Track
In the optimal arrangement, the number of cars will be distributed as evenly as possible.
In the optimal arrangement, the number of traffic cars will be distributed as evenly as possible, i.e., $$$\lvert a_i-a_j\rvert\leq 1$$$ for each valid $$$(i,j)$$$.
Let's sort the array in non-decreasing order. Let $$$a_1=p$$$, $$$a_n=q$$$, $$$p\leq q-2$$$, $$$x$$$ elements of the array be equal to $$$p$$$, $$$y$$$ elements of the array be equal to $$$q$$$, $$$\displaystyle\sum\limits_{i=x+1}^{n-y}\sum\limits_{j=i+1}^{n-y} a_j-a_i=r$$$ and $$$\displaystyle\sum\limits_{i=x+1}^{n-y} a_i=s$$$.
The inconvenience of the track will be equal to $$$S_1=r+x\cdot[s-(n-x-y)\cdot p]+y\cdot[(n-x-y)\cdot q-s]+[xy\cdot(q-p)]$$$
Suppose we increase $$$a_1$$$ by $$$1$$$ and decrease $$$a_n$$$ by $$$1$$$. Then, the number of occurrences of $$$p$$$ and $$$q$$$ will reduce by $$$1$$$, two new elements $$$p+1$$$ and $$$q-1$$$ will be formed, and $$$r$$$ and $$$s$$$ will remain unchanged. In such a case, the new inconvenience of the track will be $$$S_2=r+(x-1)\cdot[s-(n-x-y)\cdot p]$$$ $$$+(y-1)\cdot[(n-x-y)\cdot q-s]$$$ $$$+[(x-1)\cdot(y-1)\cdot(q-p)]$$$ $$$+[s-(n-x-y)\cdot(p+1)]$$$ $$$+[(n-x-y)\cdot(q-1)-s]$$$ $$$+[(y-1)\cdot(q-p-1)]$$$ $$$+[(x-1)\cdot(q-p-1)]$$$ $$$+(x-1)+(y-1)+(q-p-2)$$$
Change in inconvenience, $$$\Delta = S_1-S_2 = [s-(n-x-y)\cdot p]+[(n-x-y)\cdot q-s]+[(x+y-1)\cdot(q-p)]$$$ $$$-[s-(n-x-y)\cdot(p+1)]$$$ $$$-[(n-x-y)\cdot (q-1)-s]$$$ $$$-[(y-1)\cdot(q-p-1)]$$$ $$$-[(x-1)\cdot(q-p-1)]$$$ $$$-(x-1)-(y-1)-(q-p-2)$$$ $$$=2\cdot(n-x-y)+(x+y-1)\cdot(q-p)-(x+y-2)\cdot(q-p-1)-(x-1)-(y-1)-(q-p-2)$$$ $$$=2\cdot(n-x-y)+(q-p)+(x+y-1)-1-(x-1)-(y-1)-(q-p-2)$$$ $$$=2\cdot(n-x-y+1) > 0$$$ as $$$x+y\leq n$$$.
So, it follows that if $$$p\leq q-2$$$. it is always beneficial to move a traffic car from the sub-track with the highest number of traffic cars to the sub-track with the lowest number of traffic cars. If $$$p=q-1$$$, applying this operation won't change the inconvenience as this will only swap the last and the first element of the array leaving everything else unchanged. If $$$p=q$$$, all the elements of the array are already equal, meaning that we have $$$0$$$ inconvenience which is the minimum possible. So, there is no point in applying any operation.
Now that we have constructed the optimal arrangement of traffic cars, let's find out the value of minimum inconvenience of this optimal arrangement. Finding it naively in $$$\mathcal{O}(n^2)$$$ will time out.
Notice that in the optimal arrangement we will have some (say $$$x$$$) elements equal to some number $$$p+1$$$ and the other $$$(n-x)$$$ elements equal to $$$p$$$. Let the sum of all elements in $$$a$$$ be $$$sum$$$. Then, $$$x=sum\bmod n$$$ and $$$p=\bigg\lfloor\dfrac{sum}{n}\bigg\rfloor$$$. For each pair $$$(p,p+1)$$$, we will get an absolute difference of $$$1$$$ and for all other pairs, we will get an absolute difference of $$$0$$$. Number of such pairs with difference $$$1$$$ is equal to $$$x\cdot(n-x)$$$. So, the minimum inconvenience we can achieve is equal to $$$x\cdot(n-x)$$$. That's all we need to find out!
$$$\mathcal{O}(n)$$$
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int a[n];
long long s=0;
for(int i=0;i<n;i++)
{
cin >> a[i];
s+=a[i];
}
long long k = s%n;
long long ans = k*(n-k);
cout << ans << '\n';
}
}
C: Need for Pink Slips
Did you notice that $$$v\geq 0.1$$$?
The probability of drawing a pink slip can never decrease.
What would be the complexity of a bruteforce solution?
Make sure to account for precision errors while comparing floating point numbers.
Bruteforce over all the possible drawing sequences until we are sure to get a pink slip, i.e., until the probability of drawing a pink slip becomes $$$1$$$.
Whenever we draw a reward other than a pink slip,
- If $$$a\leq v$$$, one of the rewards becomes invalid, reducing $$$x$$$ by $$$1$$$ and this can happen at most $$$2$$$ times during the whole process.
- Else, the probability of drawing a pink slip increases by $$$\dfrac{v}{2}$$$.
Notice that the probability of drawing a pink slip can never decrease.
Now, since $$$v\geq 0.1$$$, each time we make a draw of the second type, the probability of drawing a pink slip increases by at least $$$0.05$$$. It will reach $$$1$$$ after just $$$20$$$ such draws. So, there will be at most $$$d=22$$$ draws before we are sure to get a pink slip.
Simulating the whole process will take $$$\mathcal{O}(2^d)$$$ time which is sufficient in our case.
What's left is just implementing the bruteforce solution taking care of precision errors while dealing with floating point numbers, especially while comparing $$$a$$$ with $$$v$$$ as this can completely change things up, keeping an item valid when it should become invalid. It follows that an error approximation of 1e-6 or smaller is sufficient while comparing any two values because all the numbers in the input have at most $$$4$$$ decimal places. Another alternative is to convert floating point numbers given in the input to integers using a scaling factor of $$$10^6$$$.
$$$\mathcal{O}\big(2^{\frac{2}{v}}\big)$$$
#include <bits/stdc++.h>
using namespace std;
const long double eps = 1e-9;
const long double scale = 1e+6;
long double expectedRaces(int c,int m,int p,int v)
{
long double ans = p/scale;
if(c>0)
{
if(c>v)
{
if(m>0)
ans += (c/scale)*(1+expectedRaces(c-v,m+v/2,p+v/2,v));
else
ans += (c/scale)*(1+expectedRaces(c-v,0,p+v,v));
}
else
{
if(m>0)
ans += (c/scale)*(1+expectedRaces(0,m+c/2,p+c/2,v));
else
ans += (c/scale)*(1+expectedRaces(0,0,p+c,v));
}
}
if(m>0)
{
if(m>v)
{
if(c>0)
ans += (m/scale)*(1+expectedRaces(c+v/2,m-v,p+v/2,v));
else
ans += (m/scale)*(1+expectedRaces(0,m-v,p+v,v));
}
else
{
if(c>0)
ans += (m/scale)*(1+expectedRaces(c+m/2,0,p+m/2,v));
else
ans += (m/scale)*(1+expectedRaces(0,0,p+m,v));
}
}
return ans;
}
int main()
{
int t;
cin >> t;
while(t--)
{
long double cd,md,pd,vd;
cin >> cd >> md >> pd >> vd;
int c = round(cd*scale);
int m = round(md*scale);
int p = round(pd*scale);
int v = round(vd*scale);
long double ans = expectedRaces(c,m,p,v);
cout << setprecision(12) << fixed << ans << '\n';
}
}
D1: RPD and Rap Sheet (Easy Version)
In this version, $$$x\oplus z=y$$$ or in other words, $$$z=x\oplus y$$$ where $$$\oplus$$$ is the Bitwise XOR operator.
The number of queries allowed is equal to the number of possible initial passwords.
The grader provides us no information other than whether our guess was correct or not. So, we need to find a way to ask queries such that the $$$x$$$-th query will give the correct answer if the original password was $$$(x-1)$$$.
Try to ask queries in such a way that the $$$i$$$-th query reverses the effect of the $$$(i-1)$$$-th query and simultaneously checks if the initial password was $$$(i-1)$$$.
Try to use the self-inverse property of Bitwise XOR, i.e., $$$a\oplus a=0$$$.
In this version of the problem, $$$k=2$$$. So, the $$$k$$$-itwise XOR is the same as Bitwise XOR.
In case of incorrect guess, the system changes password to $$$z$$$ such that $$$x\oplus z=y$$$. Taking XOR with $$$x$$$ on both sides, $$$x\oplus x\oplus z=x\oplus y\implies z=x\oplus y$$$ because we know that $$$x\oplus x = 0$$$.
Since the original password is less than $$$n$$$ and we have $$$n$$$ queries, we need to find a way to make queries such that if the original password was $$$(x-1)$$$, then the $$$x$$$-th query will be equal to the current password. There are many different approaches. I will describe two of them.
Let $$$q_i$$$ denote the $$$i$$$-th query. Then,
- $$$q_1=0$$$.
- $$$q_i=(i-1)\oplus (i-2)$$$ for $$$2\leq i\leq n$$$.
Let's see why this works.
Claim — If the original password was $$$x$$$, after $$$i$$$ queries, the current password will be $$$x\oplus (i-1)$$$.
Let's prove this by induction.
Base Condition — After $$$1$$$-st query, the password becomes $$$x\oplus 0=x\oplus(1-1)$$$.
Induction Hypothesis — Let the password after $$$i$$$-th query be $$$x\oplus (i-1)$$$.
Inductive step — The $$$(i+1)$$$-th query will be $$$i\oplus(i-1)$$$. If this is not equal to the current password, the password will change to $$$(x\oplus(i-1))\oplus(i\oplus(i-1))$$$ $$$=x\oplus(i-1)\oplus i\oplus(i-1)$$$ $$$=x\oplus i$$$ $$$=x\oplus((i+1)-1)$$$.
Hence, proved by induction.
Now notice that after $$$x$$$ queries, the password will become $$$x\oplus(x-1)$$$. And our $$$(x+1)$$$-th query will be $$$x\oplus(x-1)$$$ which is the same as the current password. So, the problem will be solved after $$$(x+1)$$$ queries. Since $$$0\leq x < n$$$, the problem will be solved in at most $$$n$$$ queries.
Again, let $$$q_i$$$ denote the $$$i$$$-th query. Then,
$$$q_i=(i-1)\oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{i-2} \oplus q_{i-1}$$$
Let's see why this works.
Claim — If the original password was $$$x$$$, after $$$i$$$ queries, the current password will be $$$x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{i-1} \oplus q_{i}$$$.
Let's prove this by induction.
Base Condition — The first query is $$$0$$$. After $$$1$$$-st query, the password becomes $$$x\oplus 0=x\oplus q_1$$$.
Induction Hypothesis — Let the password after $$$i$$$-th query be $$$x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{i-1} \oplus q_{i}$$$.
Inductive step — The $$$(i+1)$$$-th query will be $$$q_{i+1}$$$. So, the password after $$$(i+1)$$$-th query will be $$$(x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{i-1} \oplus q_{i})\oplus q_{i+1}$$$ $$$= x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{i-1} \oplus q_{i}\oplus q_{i+1}$$$.
Hence, proved by induction.
Now notice that after $$$x$$$ queries, the password will become $$$x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{x-1} \oplus q_{x}$$$. And our $$$(x+1)$$$-th query will be $$$x \oplus q_1 \oplus q_2 \oplus \ldots \oplus q_{x-1} \oplus q_{x}$$$ which is the same as the current password. So, the problem will be solved after $$$(x+1)$$$ queries. Since $$$0\leq x < n$$$, the problem will be solved in at most $$$n$$$ queries.
But we are not done yet. We can't afford to calculate the value of each query naively in $$$\mathcal{O}(n)$$$ because this will time out. To handle this, we need to maintain a prefix XOR whose value will be $$$p=q_1\oplus q_2\oplus \ldots \oplus q_{i-1} \oplus q_i$$$ after $$$i$$$ queries. For the $$$(i+1)$$$-th query, find $$$q_{i+1}=p\oplus i$$$ and update $$$p=p\oplus q_{i+1}$$$.
$$$\mathcal{O}(n)$$$ or $$$\mathcal{O}(n\cdot \log_{2} n)$$$ depending upon the implementation.
#include <bits/stdc++.h>
using namespace std;
int main()
{
int t=1;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
for(int i=0;i<n;i++)
{
if(i==0)
cout << 0 << endl;
else
cout << (i^(i-1)) << endl;
int v;
cin >> v;
if(v==1)
break;
}
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int main()
{
int t=1;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
int p=0;
for(int i=0;i<n;i++)
{
int q=p^i;
cout << q << endl;
p=p^q;
int v;
cin >> v;
if(v==1)
break;
}
}
return 0;
}
D2: RPD and Rap Sheet (Hard Version)
The generalised $$$k$$$-itwise XOR does not satisfy the Self-Inverse property. So, the solution for the Easy Version won't work here.
Any property which is satisfied by $$$k$$$-its will also be satisfied by base $$$k$$$ numbers since a base $$$k$$$ number is nothing but a concatenation of $$$k$$$-its. So, try to prove properties for $$$k$$$-its as they are easier to work with.
Let $$$x_j$$$ denote the $$$j$$$-th $$$k$$$-it of $$$x$$$. Then, $$$x_j\oplus_k z_j=y_j$$$ $$$\forall$$$ valid $$$j$$$. Simplifying this,
$$$x_j\oplus_k z_j=y_j$$$ $$$\implies$$$ $$$(x_j+z_j)\bmod k=y_j$$$ $$$\implies$$$ $$$z_j=(y_j-x_j)\bmod k$$$ $$$\implies$$$ $$$z_j=(y_j\ominus_k x_j)$$$ where $$$a\ominus_k b$$$ operation is defined as $$$a\ominus_k b=(a-b)\bmod k$$$.
See Hints 2, 3 and 4 of the Easy Version.
Try to generalise the solutions for easy version by exploring properties of $$$\oplus_k$$$ and $$$\ominus_k$$$ operators.
Note — It is strongly recommended to read the proofs also to completely understand why the solutions work.
The solutions described for the easy version won't work here because the general $$$k$$$-itwise operation does not satisfy self-inverse property, i.e., $$$a\oplus_k a\neq 0$$$.
In this whole solution, we will work in base $$$k$$$ only and we will convert the numbers to decimal only for I/O purpose. Notice that any property which is satisfied by $$$k$$$-its will also be satisfied by base $$$k$$$ numbers since a base $$$k$$$ number is nothing but a concatenation of $$$k$$$-its.
When we make an incorrect guess, the system changes the password to $$$z$$$ such that $$$x\oplus_k z=y$$$. Let's denote the $$$j$$$-th $$$k$$$-it of $$$x$$$ by $$$x_j$$$. Expanding this according to the definition of $$$k$$$-itwise XOR, for all individual $$$k$$$-its $$$(x_j+z_j)\bmod k=y_j$$$ $$$\implies z_j=(y_j-x_j)\bmod k$$$. So, let's define another $$$k$$$-itwise operation $$$a\ominus_k b$$$ $$$= (a-b)\bmod k$$$. Then, $$$z=y\ominus_k x$$$. Now, let's extend the solutions of the Easy Version for this version.
Before moving to the solution, let's see some properties of the $$$\ominus_k$$$ operation over $$$k$$$-its.
Property 1 — $$$(a\ominus_k b)\ominus_k(a\ominus_k c)=c\ominus_k b$$$
$$$(a\ominus_k b)\ominus_k(a\ominus_k c)$$$ $$$= ((a-b)\bmod k - (a-c)\bmod k)\bmod k$$$ $$$=(a-b-a+c)\bmod k$$$ $$$=(c-b)\bmod k$$$ $$$= c\ominus_k b$$$
Property 2 — $$$(b\ominus_k a)\ominus_k(c\ominus_k a)=b\ominus_k c$$$
$$$(b\ominus_k a)\ominus_k(c\ominus_k a)$$$ $$$= ((b-a)\bmod k - (c-a)\bmod k)\bmod k$$$ $$$=(b-a-c+a)\bmod k$$$ $$$=(b-c)\bmod k$$$ $$$= b\ominus_k c$$$
Solution -
Let $$$q_i$$$ denote the $$$i$$$-th query. Then,
- $$$q_1=0$$$,
- $$$q_i=(i-2)\ominus_k (i-1)$$$ if $$$i$$$ is even and
- $$$q_i=(i-1)\ominus_k (i-2)$$$ if $$$i$$$ is odd.
Let's see why this works.
Claim — If the original password was $$$x$$$, after $$$i$$$ queries, the password becomes
- $$$x\ominus_k (i-1)$$$ if $$$i$$$ is even and
- $$$(i-1)\ominus_k x$$$ if $$$i$$$ is odd.
Let's prove this by induction.
Base Case — $$$q_1=0$$$. So, after $$$1$$$-st query, the password becomes $$$0\ominus_k x = (1-1)\ominus_k x$$$.
Case 1 — $$$i$$$ is even
Induction hypothesis — Let the current password after $$$i$$$ queries be $$$x\ominus_k (i-1)$$$.
Inductive step — $$$(i+1)$$$ is odd. So, the $$$(i+1)$$$-th query is $$$i\ominus_k (i-1)$$$. The new password will be $$$(i\ominus_k (i-1))\ominus_k(x\ominus_k (i-1))$$$ $$$= i\ominus_k x$$$ by Property 2.
Case 2 — $$$i$$$ is odd
Induction hypothesis — Let the current password after $$$i$$$ queries be $$$(i-1)\ominus_k x$$$.
Inductive step — $$$(i+1)$$$ is even. So, the $$$(i+1)$$$-th query is $$$(i-1)\ominus_k i$$$. The new password will be $$$((i-1)\ominus_k i)\ominus_k((i-1)\ominus_k x)$$$ $$$= x\ominus_k i$$$ by Property 1.
Hence, proved by induction.
Now notice that after $$$x$$$ queries, the password will become $$$x\ominus_k (x-1)$$$ if $$$x$$$ is even or $$$(x-1)\ominus_k x$$$ if $$$x$$$ is odd which will be equal to the $$$(x+1)$$$-th query. Hence, the problem will be solved after exactly $$$(x+1)$$$ queries. Since $$$0\leq x < n$$$, the problem will be solved after at most $$$n$$$ queries.
Again, let's denote the $$$i$$$-th query by $$$q_i$$$.
Then, $$$q_i=q_{i-1}\ominus_k\bigg[q_{i-2}\ominus_k\Big[q_{i-3}\ominus_k\ldots\ominus_k\big[q_2\ominus_k[q_1\ominus_k(i-1)]\big]\ldots\Big]\bigg]$$$
Let's see why this works.
Claim — If the original password was $$$x$$$, after $$$i$$$ queries, the password will be $$$q_{i}\ominus_k\bigg[q_{i-1}\ominus_k\Big[q_{i-2}\ominus_k\ldots\ominus_k\big[q_2\ominus_k[q_1\ominus_k x]\big]\ldots\Big]\bigg]$$$
Let's prove this by induction.
Base Case — After the $$$1$$$-st query which is $$$0$$$, the password will be $$$0\ominus_k x = q_1\ominus_k x$$$.
Induction hypothesis — Let the password after $$$i$$$ queries be $$$q_{i}\ominus_k\bigg[q_{i-1}\ominus_k\Big[q_{i-2}\ominus_k\ldots\ominus_k\big[q_2\ominus_k[q_1\ominus_k x]\big]\ldots\Big]\bigg]$$$
Inductive Step — The $$$(i+1)$$$-th query is $$$q_{i+1}$$$. After $$$(i+1)$$$ queries, the password will becomes $$$q_{i+1}\ominus_k\Bigg[q_{i}\ominus_k\bigg[q_{i-1}\ominus_k\Big[q_{i-2}\ominus_k\ldots\ominus_k\big[q_2\ominus_k[q_1\ominus_k x]\big]\ldots\Big]\bigg]\Bigg]$$$
Hence, proved by induction.
Now notice that after $$$x$$$ queries, the password will become $$$q_{x}\ominus_k\bigg[q_{x-1}\ominus_k\Big[q_{x-2}\ominus_k\ldots\ominus_k\big[q_2\ominus_k[q_1\ominus_k x]\big]\ldots\Big]\bigg]$$$ which will be equal to the $$$(x+1)$$$-th query. Hence, the problem will be solved after exactly $$$(x+1)$$$ queries. Since $$$0\leq x < n$$$, the problem will be solved after at most $$$n$$$ queries.
But we are not done yet. This solution is $$$\mathcal{O}(n^2)$$$ which will time out. The solution for this isn't as simple as what we did for the Easy version because the $$$\ominus_k$$$ operation is neither associative nor commutative. So, it's time to explore some more properties of these operations.
Property 3 — $$$a\ominus_k(b\ominus_k c) = (a\ominus_k b)\oplus_k c$$$
$$$a\ominus_k(b\ominus_k c)$$$ $$$= (a-(b-c)\bmod k)\bmod k$$$ $$$= (a-b+c)\bmod k$$$ $$$= ((a-b)\bmod k+c)\bmod k$$$ $$$= (a\ominus_k b)\oplus_k c$$$
Property 4 — $$$a\ominus_k(b\oplus_k c) = (a\ominus_k b)\ominus_k c$$$
$$$a\ominus_k(b\oplus_k c)$$$ $$$= (a-(b+c)\bmod k)\bmod k$$$ $$$= (a-b-c)\bmod k$$$ $$$= ((a-b)\bmod k-c)\bmod k$$$ $$$= (a\ominus_k b)\ominus_k c$$$
Now, let's try to simplify our queries.
- $$$q_1=0$$$
- $$$q_2=q_1\ominus_k 1$$$
- $$$q_3=q_2\ominus_k [q_1\ominus_k 2]=[q_2\ominus_k q_1]\oplus_k 2$$$ (by Property 3)
- $$$q_4=q_3\ominus_k \big[q_2\ominus_k [q_1\ominus_k 3]\big]=q_3\ominus_k \big[[q_2\ominus_k q_1]\oplus_k 3\big]=\big[q_3\ominus_k[q_2\ominus_k q_1]\big]\ominus_k 3$$$ (by Property 4)
- $$$\ldots$$$
See the pattern?
You can generalize the $$$i$$$-th query as -
- $$$q_i=q_{i-1}\ominus_k\Big[q_{i-2}\ominus_k\big[q_{i-3}\ominus_k\ldots\ominus_k[q_2\ominus_k q_1]\ldots\big]\Big]\oplus_k (i-1)$$$ if $$$i$$$ is odd
- $$$q_i=q_{i-1}\ominus_k\Big[q_{i-2}\ominus_k\big[q_{i-3}\ominus_k\ldots\ominus_k[q_2\ominus_k q_1]\ldots\big]\Big]\ominus_k (i-1)$$$ if $$$i$$$ is even
So, we will maintain a prefix Negative XOR whose value after $$$i$$$ queries will be $$$p=q_{i}\ominus_k\Big[q_{i-1}\ominus_k\big[q_{i-2}\ominus_k\ldots\ominus_k[q_2\ominus_k q_1]\ldots\big]\Big]$$$
Then,
- $$$q_{i+1}=p\ominus_k i$$$ if $$$i$$$ is odd
- $$$q_{i+1}=p\oplus_k i$$$ if $$$i$$$ is even
Then update $$$p=q_{i+1}\ominus_k p$$$
- Both the operations $$$\ominus_k$$$ and $$$\oplus_k$$$ can be implemented naively by converting the decimal numbers to base $$$k$$$, finding the $$$k$$$-itwise XOR of the base $$$k$$$ numbers and finally converting it back to decimal. The time complexity for each of these operations will be $$$\mathcal{O}(\log_k n)$$$.
- At any stage, the maximum number that we could be dealing with will be non-negative and will not exceed $$$n\times k$$$ as the $$$k$$$-itwise operations do not add extra $$$k$$$-its. This fits well within the limits of $$$y$$$ which is $$$2\cdot 10^7$$$.
- The total time complexity of the solution will be $$$\mathcal{O}(n\log_k n)$$$.
#include <bits/stdc++.h>
using namespace std;
int knxor(int x,int y,int k)
{
int z=0;
int p=1;
while(x>0 || y>0)
{
int a=x%k;
x=x/k;
int b=y%k;
y=y/k;
int c=(a-b+k)%k;
z=z+p*c;
p=p*k;
}
return z;
}
int main()
{
int t=1;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
for(int i=0;i<n;i++)
{
if(i==0)
cout << 0 << endl;
else if(i%2==0)
cout << knxor(i,i-1,k) << endl;
else
cout << knxor(i-1,i,k) << endl;
int v;
cin >> v;
if(v==1)
break;
}
}
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int knxor(int x,int y,int k)
{
int z=0;
int p=1;
while(x>0 || y>0)
{
int a=x%k;
x=x/k;
int b=y%k;
y=y/k;
int c=(a-b+k)%k;
z=z+p*c;
p=p*k;
}
return z;
}
int kxor(int x,int y,int k)
{
int z=0;
int p=1;
while(x>0 || y>0)
{
int a=x%k;
x=x/k;
int b=y%k;
y=y/k;
int c=(a+b)%k;
z=z+p*c;
p=p*k;
}
return z;
}
int main()
{
int t=1;
cin >> t;
while(t--)
{
int n,k;
cin >> n >> k;
int p=0;
for(int i=0;i<n;i++)
{
if(i==0)
cout << 0 << endl;
else if(i%2==0)
{
int q = kxor(p,i,k);
cout << q << endl;
p=knxor(q,p,k);
}
else
{
int q = knxor(p,i,k);
cout << q << endl;
p=knxor(q,p,k);
}
int v;
cin >> v;
if(v==1)
break;
}
}
return 0;
}
This part may be interesting for hackers and those who would like to understand what goes in the background checkers and interactors which determine the correctness of their solutions.
You must have noticed a large number of submissions failing on Test 1 itself. If you check the checker logs of those solutions, you will find that they fail on many different test cases although the test itself has 1 or 2 test cases. This is because the grader is also adaptive apart from the Rap Sheet System being adaptive. The initial password is not fixed and the grader checks if the solution will give correct answer or not for all possible initial passwords in just a single run! Here is how this is implemented.
The grader maintains a set which initially contains all possible initial passwords. Whenever you ask a query, the grader finds out which initial password will give correct answer for this query. This is found using the generalised expression of queries derived in the Method 2 solution. Take some time to convince yourself that this initial password will be unique. It then removes this initial password from the set if it still exists. After that, if the set is empty, the grader returns 1 (meaning that there is no other password for which the solution can give Wrong Answer), otherwise 0 (obviously after checking the constraints on $$$y$$$). In this way, only a solution which gives correct answers for all possible initial passwords for a particular $$$n$$$ and $$$k$$$ defined in the input will manage to pass.
Sometimes, checkers and adaptive interactors are more difficult to write than the solution itself! This was one such case.
E: The Final Pursuit
In a simple $$$n$$$-Dimensional Hypercube, two vertices are connected if and only if they differ by exactly $$$1$$$ bit in their binary representation.
The $$$n$$$-Dimensional Hypercubes are highly symmetric and all vertices are equivalent.
If we select a particular vertex, then all directions in which the edges connected to it goes are also equivalent.
For any two vertices $$$a$$$ and $$$b$$$ separated at a distance of exactly $$$2$$$, there are exactly $$$2$$$ vertices connected to both $$$a$$$ and $$$b$$$.
Any permuted $$$n$$$-Dimensional Hypercube is isomorphic to the simple $$$n$$$-Dimensional Hypercube. So, its structure is same as the simple $$$n$$$-Dimensional Hypercube.
You can find the permutation greedily
Before moving to the solution, notice a very important property of simple $$$n$$$-Dimensional Hypercubes — Two vertices $$$a$$$ and $$$b$$$ are connected if and only if $$$a$$$ and $$$b$$$ differ by exactly one bit in their binary representations.
The permutation can be found using the following greedy algorithm — First, assign any arbitrary vertex as $$$p_0$$$. This is obvious since all vertices are equivalent. Then, in the simple $$$n$$$-Dimensional Hypercube, all powers of $$$2$$$ must be connected to the vertex $$$0$$$. Moreover, these vertices are added only when we are adding another dimension to the cube. Since all directions are also equivalent, it does not matter in which direction we add a new dimension. So, we can assign all the $$$n$$$ vertices connected to $$$p_0$$$ in the permuted $$$n$$$-Dimensional Hypercube as $$$p_1$$$, $$$p_2$$$, $$$p_4$$$, $$$p_8$$$, $$$\ldots$$$, $$$p_{2^{n-1}}$$$ in any arbitrary order. Now, we will find $$$p_u$$$ for the remaining vertices in increasing order of $$$u$$$.
In order to find $$$p_u$$$, first find a set $$$S$$$ of vertices $$$v$$$ such that $$$v < u$$$ and $$$v$$$ is connected to $$$u$$$ in the simple $$$n$$$-Dimensional Hypercube. Then find any vertex $$$w$$$ connected to all the vertices $$$p_v$$$ such that $$$v\in S$$$ in the permuted $$$n$$$-Dimensional Hypercube and assign $$$p_u=w$$$. I claim that we can never make a wrong choice because we will never have a choice! There will only be one such vertex $$$w$$$ for any $$$u$$$. Let's prove it.
Consider two vertices $$$v_1$$$ and $$$v_2$$$ in the set $$$S$$$. These vertices will differ by exactly $$$2$$$ bits in their binary representation. Let the bits in which they differ be $$$b_x$$$ and $$$b_y$$$. Then, they will have the form $$$v_1=\ldots b_x\ldots b_y\ldots$$$ and $$$v_2=\ldots b^{'}_{x}\ldots b^{'}_{y}\ldots$$$ where $$$\ldots$$$ represent the same bits. Now, only two vertices $$$u_1=\ldots b_{x}\ldots b^{'}_{y}\ldots$$$ and $$$u_2=\ldots b^{'}_{x}\ldots b_{y}\ldots$$$ can be connected to both $$$v_1$$$ and $$$v_2$$$. Since a permuted $$$n$$$-Dimensional Hypercube is isomorphic to a simple $$$n$$$-Dimensional Hypercube, there will only be two vertices connected to both $$$p_{v_1}$$$ and $$$p_{v_2}$$$ in the permuted $$$n$$$-Dimensional Hypercube also.
If we iterate over $$$u$$$ in increasing order, then $$$b_x\neq b_y$$$, otherwise one of $$$v_1$$$ or $$$v_2$$$ will be greater than $$$u$$$ which is a contradiction. So, the only vertices connected to both $$$v_1$$$ and $$$v_2$$$ will have the forms $$$u_1=\ldots 0\ldots 0\ldots$$$ and $$$u_2=\ldots 1\ldots 1\ldots$$$. Now since $$$u_1<v_1$$$ and $$$u_1<v_2$$$, $$$p_{u_1}$$$ has already been calculated and so, one of the vertex connected to both $$$p_{v_1}$$$ and $$$p_{v_2}$$$ in the permuted $$$n$$$-Dimensional Hypercube has already been used. So, we are left with only one choice for such a vertex $$$w$$$.
Let's call the vertex connected to a given vertex and which is in the opposite constituent smaller hypercube the image of the given vertex.
Lemma — if there is an edge $$$(a, b)$$$ in the $$$n$$$-Dimensional hypercube where vertices $$$a$$$ and $$$b$$$ lie in different constituent $$$(n-1)$$$-Dimensional Hypercubes (in other words, $$$a$$$ and $$$b$$$ are images of each other), then for all vertices $$$q$$$ adjacent to $$$a$$$, the image of $$$q$$$ is adjacent to $$$b$$$.
This lemma can be proved by using the fact that two vertex are connected if and only if they differ by exactly $$$1$$$ bit.
Select any two vertices $$$a$$$ and $$$b$$$. They form a starting point: we treat them as two vertices in opposite constituents (by symmetry, we can prove that any pairs can be treated as such).
Now let us perform multisource BFS with $$$a$$$ and $$$b$$$ as source nodes. Due to the lemma, the nodes which are discovered from $$$a$$$ first lie in the component of $$$a$$$, and those which are discovered from $$$b$$$ first lie in the component of $$$b$$$ (it is easy again to prove it using induction on depth of already discovered vertices). So we have separated these two constituent smaller dimension hypercubes. Lets call a recursive function on any one of them: this recursive function returns a permutation which transforms the permutated hypercube to the simple hypercube. Now, we find for each vertex, in the constituent hypercube whose permutation we just found, its image. Then we can find the permutation for the other constituent by just adding $$$2^{n-1}$$$ to the corresponding image. Hence we perform the merging process of recursion.
The time complexity of this approach is $$$\mathcal{O}(n\cdot 2^{n})$$$
Instead of colouring the permuted $$$n$$$-Dimensional Hypercube, try to colour the simple $$$n$$$-Dimensional Hypercube and map these colours to the permuted one in the end using the permutation found in Part 1.
The number of vertices of each colour will be equal.
Try to colour a simple $$$4$$$-Dimensional Hypercube. This is not a graph problem, rather a constructive problem.
The way in which vertices are connected in a simple $$$n$$$-Dimensional Hypercube suggests something related to Bitwise XOR.
Let's try to colour the simple $$$n$$$-Dimensional Hypercube instead of the permuted one. We can map the colours to the permuted one in the end using the permutation found in Part 1.
I claim that if $$$n$$$ is not a power of $$$2$$$, then no colouring exists. A simple explanation is that the graph is symmetric and also the colours. So, it is natural that the number of vertices of each colour must be equal meaning $$$2^n$$$ must be divisible by $$$n$$$ or in other words, $$$n$$$ must be a power of $$$2$$$ itself. But if symmetry doesn't satisfy you, I have a formal proof too.
According to the condition, every vertex must be connected to at least one vertex of every colour or equivalently, exactly one vertex of every colour since there are $$$n$$$ colours and $$$n$$$ neighbours of each vertex. So, if we consider the set of neighbours of any vertex, every colour will appear exactly once in that set. If we consider the multi-set of neighbours of all vertices, every colour will appear $$$2^n$$$ times in that set. But every vertex has been counted $$$n$$$ times in this multi-set because a particular vertex is the neighbour of $$$n$$$ other vertices. So, if we consider the set of all vertices, every colour will appear $$$\frac{2^n}{n}$$$ times in that set. Obviously, this number must be a whole number. So, $$$2^n$$$ must be divisible by $$$n$$$ or in other words, $$$n$$$ must itself be a power of $$$2$$$ for a colouring to exist. Otherwise, it doesn't exist. To show that a colouring exists if $$$n$$$ is a power of $$$2$$$, we will construct a colouring.
Construction - This is the most interesting and difficult part of the whole problem. The following construction works —
Consider a vertex $$$u$$$. Let its binary representation be $$$b_{n-1}b_{n-2}\ldots b_2 b_1 b_0$$$. Then the colour of this vertex will be $$$\bigoplus\limits_{i=0}^{n-1} i\cdot b_i$$$. Let's show why this works.
- $$$\bigoplus\limits_{i=0}^{n-1} i\cdot b_i$$$ will always lie between $$$0$$$ and $$$n-1$$$ inclusive because $$$n$$$ is a power of $$$2$$$.
- If we are at a vertex $$$u$$$ with a colour $$$c_1$$$ and we want to reach a vertex of colour $$$c_2$$$, we can reach the vertex $$$v=u\oplus(1\ll (c_1\oplus c_2))$$$. This is a vertex adjacent to $$$u$$$ since it differs from it by exactly $$$1$$$ bit and this is the $$$(c_1\oplus c_2)$$$-th bit. Notice that the colour of this vertex $$$v$$$ will be $$$c_1\oplus (c_1\oplus c_2) = c_2$$$.
- $$$(c_1\oplus c_2)$$$ will always lie between $$$0$$$ and $$$n-1$$$ because $$$n$$$ is a power of $$$2$$$. So, $$$v$$$ will always be a valid vertex number.
You can see that many of these facts break when $$$n$$$ is not a power of $$$2$$$. So, this colouring will not work in such cases.
Finally, after colouring the simple hypercube, we need to restore the vertex numbers of the permuted hypercube. This can be simply done by replacing all vertices $$$u$$$ with $$$p_u$$$ using the permutation we found in Part 1.
Well, that's enough of theoretical stuff. For those who like visualising things, here is a 4-D Hypercube and its colouring -
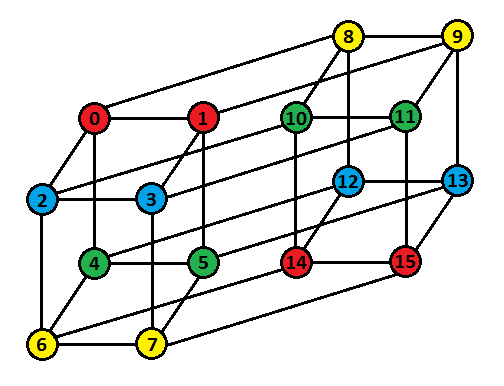
Finding the permutation takes $$$\mathcal{O}(n\cdot\log_2 n\cdot 2^n)$$$ time if implemented using set or $$$\mathcal{O}(n^2\cdot 2^n)$$$ time if implemented using vector. Constructing the colouring for the simple $$$n$$$-Dimensional Hypercube takes $$$\mathcal{O}(n\cdot 2^n)$$$ time. Restoring colours for the permuted $$$n$$$-Dimensional Hypercube takes $$$\mathcal{O}(2^n)$$$ time.
So, the overall time complexity is $$$\mathcal{O}(n\cdot\log_2 n\cdot 2^n)$$$ or $$$\mathcal{O}(n^2\cdot 2^n)$$$ depending upon implementation.
#include <bits/stdc++.h>
using namespace std;
void permuteHypercube(int n,int m,vector<int> adj[],set<int> s[],int p[])
{
for(int i=0;i<m;i++)
p[i]=-1;
bool used[m];
for(int i=0;i<m;i++)
used[i]=false;
p[0]=0;
used[0]=true;
for(int u=1;u<m;u++)
{
vector<int> req;
for(int i=0;i<n;i++)
{
int v=u^(1<<i);
if(v<u)
req.push_back(v);
}
if(req.size()==1)
{
int v=req[0];
for(int i=0;i<adj[p[v]].size();i++)
{
int w=adj[p[v]][i];
if(used[w])
continue;
p[u]=w;
used[w]=true;
break;
}
}
else
{
int v=req[0];
for(int i=0;i<adj[p[v]].size();i++)
{
int w=adj[p[v]][i];
if(used[w])
continue;
if(s[w].find(p[req[1]])!=s[w].end())
{
p[u]=w;
used[w]=true;
break;
}
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int m = (1<<n);
int p[m];
set<int> s[m];
vector<int> adj[m];
for(int i=0;i<n*m/2;i++)
{
int u,v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
s[u].insert(v);
s[v].insert(u);
}
permuteHypercube(n,m,adj,s,p);
for(int i=0;i<m;i++)
cout << p[i] << " ";
cout << '\n';
if(n!=1 && n!=2 && n!=4 && n!=8 && n!=16)
{
cout << -1 << '\n';
continue;
}
int temp[m];
for(int i=0;i<m;i++)
{
int clr=0;
for(int j=0;j<n;j++)
{
if(i&(1<<j))
clr=clr^j;
}
temp[i]=clr;
}
int c[m];
for(int i=0;i<m;i++)
c[p[i]]=temp[i];
for(int i=0;i<m;i++)
cout << c[i] << " ";
cout << '\n';
}
}
#include <iostream>
#include <iomanip>
#include <vector>
#include <cmath>
#include <algorithm>
#include <set>
#include <utility>
#include <queue>
#include <map>
#include <assert.h>
#include <stack>
#include <string>
#include <ctime>
#include <chrono>
#include <random>
using namespace std;
const int MAX=65536;
int power[21]={0};
vector<int> adj[MAX+1];
bool xtra[MAX+1];
bool in[MAX+1];
vector<int> f(vector<int> s)
//given a set of vertices [graph], returns the permutation that was applied to the simple hypercube to get this graph
{
/*
cout << "set\n";
for (auto it : s)
{
cout << it << " ";
}
cout << '\n';
*/
if ((int)s.size()==2)
{
vector<int> p(2);
p[0]=s[0];
p[1]=s[1];
return p;
}
for (auto i: s) in[i]=true;
int v1=s[0];
int v2=-1;
for (auto i: adj[v1])
{
if (in[i])
{
v2=i;
break;
}
}
assert(v2!=-1);
//cout << "v1= " << v1 << " v2 = " << v2 << '\n';
vector<int> component;
//multisource BFS from (v1, v2)
{
queue<int> q;
q.push(v1);
q.push(v2);
map<int, bool> vis;
vis[v1]=true;
vis[v2]=true;
map<int, bool> cmp;
cmp[v1]=true;
component.push_back(v1);
while (!q.empty())
{
auto u=q.front();
q.pop();
for (auto i: adj[u])
{
if ((!vis[i])&&in[i])
{
vis[i]=true;
q.push(i);
cmp[i]=cmp[u];
if (cmp[i]) component.push_back(i);
}
}
}
}
for (auto i: s) in[i]=false;
for (auto i: component) in[i]=true;
vector<int> p1=f(component);
for (auto i: s) in[i]=true;
for (auto i: component) xtra[i]=true;
vector<int> p((int)s.size());
int z=component.size();
assert(2*z==(int)s.size());
for (int i=0; i<z; i++) p[i]=p1[i];
for (int i=0; i<z; i++)
{
//i+z
int g=-1;
for (auto i: adj[p[i]])
{
if (in[i]&&(!xtra[i]))
{
g=i;
break;
}
}
assert(g!=-1);
p[z+i]=g;
}
for (auto i: component) xtra[i]=false;
for (auto i: s) in[i]=false;
return p;
}
vector<int> colorit(int n)
{
vector<int> ret(n);
for (int i=0; i<n; i++)
{
int res=0;
for (int z=0; z<20; z++) res^=z*((power[z]&i)!=0);
ret[i]=res;
}
return ret;
}
void solve()
{
int n;
cin>>n;
for (int i = 0; i < power[n]; i++) adj[i].clear();
for (int j = 0; j < n * power[n - 1]; j++)
{
int u, v;
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
vector<int> p;
{
vector<int> s;
for (int i=0; i<power[n]; i++) s.push_back(i);
p=f(s);
}
for (int i=0; i<power[n]; i++) cout<<p[i]<<' ';
cout<<'\n';
if (power[n]%n)
{
cout<<-1<<'\n';
return;
}
vector<int> col=colorit(power[n]);
vector<int> out(power[n]);
for (int i=0; i<power[n]; i++)
{
out[p[i]]=col[i];
}
for (int i=0; i<power[n]; i++) cout<<out[i]<<' ';
cout<<'\n';
return;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
//t=1;
power[0]=1;
for (int j=1; j<=20; j++) power[j]=power[j-1]*2;
while (t--)
{
solve();
}
return 0;
}










-
No wonder you are gray.
Video editorial of 1.A. Exciting Bets 2. B. Customising the Track
your video was helpful to me . thanks
Thanks. It means a lot :)
Problem C should be rejudged with eps = 0, author took esp = 1e-9 but 0 should have been taken ideally
It's actually common to encounter precision problems, so if you didn't know it then you should learn it and get AC when you meet float problems again.
Can u please check my latest solution it’s got problem c, I know I’ve done everything right except handle precision , can you tell me how to handle precision , thanks in advance :)
You shouldn't just use $$$>$$$ in your code, you have to add that if the difference between two floating number is less then a certain value than it should be count as equal. That number depends but in this question as the editorial says 1e-6 should be enough.
i didnt get it can u please explain what "exactly" i need to change in my code
you can change the
if (a > v)toif (a > v && abs(a-v) > 1e-6).i did it and got ac thanks :) can you kindly tell me why was it needed and how it made my code work
https://codeforces.me/blog/entry/92582?#comment-813768
yungyao Can you provide any recourse or link, or even the keyword to search for, in order to learn how to handle precision in cases like this where this advance level of understanding is required.
I learn this from my friends so I am not sure about what resources are good. I think you can just search for floating number precision problems. Anyway the point is that C++ can not handle all floating number precisely, for example
0.1 + 0.2 == 0.3will return false, so a lot of times if the difference between two floating numbers are small enough then it should be considered same.Sorry... I had a mistake in my code. eps=0 also works fine.
Did you notice the variable "scale" in the tutorial?
I like your name.(not username , but name in profile). voyager
you can find the explanation for my alternative solution for E in Tutorial: Part 1- Finding the Permutation.
I was reminded why I don't know and don't like problems which are only about doubles. Spent 2hours trying to find out why a > 0 doesn't work...
speedforces
yes, speedforces for those who solve only one problem in the round.
thought I could get wholesome rivalry, sorry for being cocky:/
it's just stupid to write "I will beat you in the future" when you are rated 600 points lower. Just shut up and work hard.
Its better to be at expert regularly giving contest than stop giving contest on becoming master once just so that you can flex .Maybe a guess or cheating.You can only become the driver of the bus of tourist,so stop putting anything related to our legend-tourist in your profile.
What the hell. I stopped writing rated contests for a while even after becoming purple. I practice on hard problems exclusively during these periods, and when I feel I can jump to the next level (IM in this case) I continue writing contests.
As for me becoming master by "fluke", in all the div2 rounds which are unrated for me I have written, I have solved 2400/2500 rated problems within the first hour. So no doubt I can maintain master if I write a contest now. But I don't want pressure of rated contests right now. Its just my personal preference.
Your comment is incredibly insulting. You probably are a low rated div3 guy and dont know what it takes to achieve what I have. And as for the guy above, he keeps on writing "I will beat you" so I got angry.
Peace.
Yeah people like you who have achieved fcuk all in their life masquerading as all intelligent when i open CF is why i hate people so much. You just got lucky with your submissions and now act as a bl**dy know it all when in reality you are just a stupid BTech kid.
Shut up and stop being a fcuking elitist.
If being lucky was the criteria for codeforces rating then I think all the LGMs should buy lottery tickets immediately.
And Leo Messi would be newbie.
The problems which get 2400/2500 in Div2 Rounds are not that difficult(they are around 2200 maybe) but the ones in Div1 like D1B-C(Rated <= 2400 usually) are much more harder. It usually happens with me, I frequently solve 2400/2500 in unofficial Div2s but can't get even close to a 2300 rated problem in Div1.
Painful but true :").
https://codeforces.me/contest/1543/submission/121576639 (A)-00:08 https://codeforces.me/contest/1543/submission/121580369 (B)-00:12 https://codeforces.me/contest/1543/submission/121614790 (C)-00-58
wtf....
from the submission time we can track when solution gets leaked ... so we need to prepare even harder ..to solve before it or near that time... so that we are not at much loss...bcz anyways they wont be banned or even if they will start again this foolishness...
Typical cheater on codeforces lol
i think he's trying to get an unreadable code so he doesn't get hacked, tho he will still fail to real cases if the solution is wrong
And that is still against the codeforces policy lmfao Read policy number 4 in Can-do's and Can't-do's section
he will fail in real — interview for sure.. as he already sold his moral values..and already failed in real life..xd
Submission A — 00:06
Submission B — 00:09
Submission C — 01:40
Submission D1 — 00:53
Is this some sort of hack??
XD WTF!
Maybe he wants to have a higher rating by this disgusting way . However , He is lack of honesty which must be kept in our daily life .
MikeMirzayanov Please ban these type of user immediately to set an example, humble request, Please :\
C was definitely the worst question, because it is a hit or miss. People who are used to this type of question would probably convert the doubles into integers/long long to prevent errors, but most people are gonna suffer from the terrible precision of long double. Aside from rambling, I think D2 is a pretty cool question nevertheless.
Well, float precision is an important skill for competitive programmers. For people that are not familiar with these kind of problems, they will learn from this.
Precision errors are unpredictable most of the time. I've seen problems where a mere change in the value of
epscreates the difference betweenAcceptedandWrong answer on test 22xD. For eg. changingepsto1e-14gives WA but1e-10works.Could you please share that task you talking about. Thank you.
It was in a gym contest I'll have to search. I'll share when I find it.
I don't get why long double gives me WA but double gives me AC. I added 1e-14 to the inputs in both cases.
Yeah why? also what does adding 1e-14 do?
adding 1e-14 to the numbers increases precision up to 14 digits and from here on every operation will be performed up to this precision. I'm not sure if this is what happens but this simple trick has worked for me in many such problems.
The same trick doesn't work if instead of adding 1e-14 we multiply by 1.00000000001 does multiplying not increase precision?
No, multiplying doesn't improve precision. In fact, it makes precision worse.
(Edit: Also, "adding 1e-9 or 1e-12" doesn't "improve" your precision. What it does is basically saying "if the probability is less than 1e-9, we'll assume it's zero". We need this because, for example, 0.3-0.2=0.09999999999999998 (you can check this in python).)
how's it hit or miss? they said 1e-6, i used 1e-6, first try
This was a fun round and figuring out how eps works finally paid itself off. Also massive props for making one of the most interesting interactives on codeforces. :)
In C, one of my pretest answer was off by 0.002, rest were correct, so I was getting wrong answer, I usually use python, did a little bit of digging up after contest when I switched from float -> Decimal class, got the right answer :/
ReadingStatementsForces
In what round do you not have to read the statement? April Fools??
When the proofs are by induction... you know it's either hit or miss.
E can be found here:
https://www.youtube.com/watch?v=as7Gkm7Y7h4
https://www.youtube.com/watch?v=wTJI_WuZSwE
It's also https://oj.uz/problem/view/IOI17_coins
Thanks for detailed editorial containing hints and multiple approaches.
In problem C, why if 0 is used in place of epsylum(very small value) in the author's solution gives a wrong answer?
Exactly that's also my question
0 is an integer and eps is a double , that is why using epsilon prevents precision errors
The problem is that when you compare two floating-point numbers, the result of the comparasion may be wrong, because computers store numbers up to a certain precision.
In this problem, when a certain probability becomes exactly 0, the respective variable may store a very small number due to precision issues, and you make an extra step due to that, changing the answer. You should always compare floating points with epsilon, unless the comparasion result is irrelevant.
How to choose a proper epsilon? That is a difficult question in general, but in this problem it is easy. Let's say that you store the probability in variable
a. I claim that the true value ofais always of the form $$$a= x\cdot 10^{-4}\cdot 2^{-steps}$$$, where $$$x$$$ is an integer and $$$steps$$$ is the number of steps made. It can be proved by induction on steps. Now it's easy to see that the true value is either $$$0$$$ or at least $$$10^{-4}\cdot 2^{-20} > 10^{-11}$$$. Given that precision issues are usually not greater than few least significant bits ($$$\approx 10^{-16}$$$ if you use long double), any epsilon between these numbers should work. It turns out that some other epsilons work too.The reference solution to this problem operates in integers, of course, and avoids these issues. It will be uploaded in the post soon.
Thank you, liked the problems! Although I thought A is too hard to be A, but it was fun:)
I have a question about my solutions. On my machine, the answer was printed, but in system I got WA. Here's my solution: 121640373. System said that on test 5 3 with start password 1 I tried five times and haven't guessed it, but when I was testing locally my program did. Can anyone please tell me why did it happen?
Thanks to kind man in technocup chat, problem solved, I thought that a xor b = z means that b equals z xor a. And this was mentioned in the editorial, so sorry for stupid question:)
I know this is generally a dumb question, but I have to ask — people who solved E, how did you come up with the colouring? Is it just a matter of throwing shit at the wall and seeing what sticks?
If you didn't like the contest, don't downvote the editorial. Just downvote the announcement.
Hello everyone, please do not downvote the editorial because you did badly or didn't like one problem from the round. Round authors and testers did their best to make the round as high-quality as possible, and you can see that they even implemented feedback to give hints inside the editorial, which is really appreciated!
Thank you JaySharma1048576 for this wonderful round!!
How could we guess to use epsilon in problems like C? Is it some rule to have it as 10^-6? I used it as 0, but my solution gave imprecise answers for 3rd test case in the sample test case. Even, the editorial solution gives the same answer as mine if epsilon was set to 0. So, I could confirm that I was getting wrong answers only because of the precision problems. Does using 1e-6 as epsilon work for other similar problems too?
I also have the same doubt. In the official solution, if we change the value of eps to 1e-17 or lower, the answer varies drastically.
Try
This will print "No"
When you must work with doubles/floats you should always test for equality with very small values such as (1e-6, or 1e-9), as opposed to 0, due to precision errors. If you compile with the -Wfloat-equal option, your compiler will automatically alert you to not test for equality with "==" or "!=" if you do in your code
no 1e-6 is often too big to find equality in pb152 of PE you would find false solution if you used such an epsilon, sadly you have to use gut feeling to guess in each problem the good epsilon. By the way I got WA on test case 4 after the round I'm very angry against myself
Really appreciate the quick and detailed editorial, it really helps to read the editorial while the problems are still fresh in your mind (if that sentence makes any sense :P). Having said that, I do think that a disclaimer that a round is gonna be more math-centric rather than algorithm based should be given as a lot of people might only enjoy algorithm based contests, but a decent round nonetheless :)
In problem C official solution, epsilon = 1e-9 is being used for checking 0 equality. However, if exact 0 equality check is used in the conditions, the solution fails by 0.03 even on pretest 1 (input 3). Can anyone please explain how do we determine what equality check to use in such questions ?
https://codeforces.me/contest/1543/submission/121632946
In C, why there are precision issues, even if I set the argument to 0 explictly? I thought 0 can be represented accurately according to IEEE 754, but it seems in the function the zero becomes a small number rather than 0.
It’s correct that literal zero has exact representation, but how do you deal with subtraction
c - vandm - vin the writer’s solution, which can result in a tiny floating point number even when it’s zero in theory?Oh I see, thank you!
Language of C could have been better. Otherwise good problems(specially interactive ones)
This is to clarify why taking epsilon equal to $$$0$$$ will not work in C. Everyone know that floating point arithmetic is associated with some precision errors which is usually of the order $$$10^{-15}$$$. So, if $$$c=v$$$, ideally $$$c$$$ should become invalid but if due to some floating point precision error, $$$c$$$ becomes $$$10^{-15}$$$ and if you are comparing it with $$$0$$$, your code will treat it as still valid and this will cause a Wrong Answer. In this problem, taking any epsilon in the range $$$10^{-6}$$$ to $$$10^{-14}$$$ will work, not only $$$10^{-9}$$$. I was well aware that many participants will make this error. So, I included a test where this error arises in the samples itself (sample test case 3) so that no one gets unnecessary penalties.
Moreover, the main solution against which the solutions are checked doesn't use floating point numbers. It uses integers after multiplying the values by a scaling factor. I am providing that solution in the editorial.
"In this problem, taking any epsilon in the range $$$10^{-6}$$$ to $$$10^{-14}$$$ will work"
@JaySharma1048576, Can you please show the proof for the above statement with all the steps!! I know I am asking for more but this kind of problem is not common(at least I encountered this for the first time) so please help!
Thanks for the great round!
Epsilon should neither be too high nor too low. In general, it should be less than the lowest significant number that may affect the answer and more than the highest precision error that may occur. $$$v$$$ has $$$4$$$ decimal places at max as given in the constraints. It follows that $$$\frac{v}{2}$$$ has $$$5$$$ decimal places at max. So, at any point when there are three valid items, $$$c$$$, $$$m$$$, and $$$p$$$ can have $$$5$$$ decimal places at max. When suppose $$$c$$$ becomes invalid, $$$\frac{c}{2}$$$ gets added to the probabilities of the remaining items which can have $$$6$$$ decimal places at max. After this, the number of decimal places in $$$m$$$ and $$$p$$$ can never go more than $$$6$$$ because all the probability will now go to $$$p$$$ only involving no division by $$$2$$$. So, at any point the maximum epsilon allowed is $$$10^{-6}$$$. If you look more carefully then the $$$5$$$-th and $$$6$$$-th decimal places will always be one of $$$00$$$, $$$25$$$, $$$50$$$ or $$$75$$$. So, the maximum epsilon allowed is in fact $$$25\cdot 10^{-6}$$$. But for simplicity, I have taken $$$10^{-6}$$$. The lower limit is, however, difficult to say. Precision errors are quite random and may be as low as $$$10^{-18}$$$ or as high as $$$10^{-15}$$$. But since double data type uses $$$52$$$ bits for mantissa, atleast $$$15$$$ decimal places of accuracy is guaranteed. So, anything greater than $$$10^{-15}$$$ must be fine for epsilon.
Please do not downvote this blog. Some people might be unable to find the editorial.
I'm kinda disappointed at problems in this round, cuz I feel they're not so relevant to Algorithm or something fun but more revelant to English Reading and Code Implementation.
I hadn't seen any problem like E before. Btw if setters never use something similar to "known" problems then will they even be known for most div2 participants?
I mostly agree with the rest though.
Well, fair enough. What I concern is, cuz it feel like a repeated problem in a sense, especially cuz it's not so relevant to a certain algorithm. I'm kinda worried about situations like someone easily solve it if he learned it before, when others with more experience in algorithm maybe can't get the point in a short time.
Btw, to author if you're seeing, I don't mean to be negative to your efforts >_<, I respect all people contributing to CF. Just want to give some suggestions to look forward to your better problems. >_<
Sure. I am not blaming you for anything. I am taking your feedback positively and I will try to improve the statements next time.
Thanks for detailed editorial containing hints and multiple approaches! ><
Hi! Guys you don't have to downvote the editorial because Author and coordinator and testers did their best to create this contest and dear Author made a great and complete editorial ! Afterall Good job everyone.
In problem A, the input constraints for a and b are 0 to 1e18. Many participants used int type variables to read a and b have verdict as Accepted. Is it because the main tests do not contain tests which are greater than INT_MAX. Example: 121578546
The solution has
#define int long longin the template.Problem C was not at all good; first and foremost, its language was as terrible as it could be. It was difficult to follow, and the variables used to describe the test cases were unclear. Simple and precise language can also be used to create a nice and fascinating problem.
A: good idea, gcd(x, y) = gcd(x — y, y) B: intuitive, greedy C: implementation D: try 0~(n-1) with previous change
Can anyone give the reason why 1 is added in the recursive solution given in the editorial of problem C in the line given below
ans += (c/scale)*(1+expectedRaces(c-v,m+v/2,p+v/2,v));
else you would get as whole answer 0, you must count future race and this particular race (which is the 1), hope I'm clear
Why is this code https://codeforces.me/contest/1543/submission/121641823 fast? Shouldn't it get TLE? Are tests bad?
C can be solved with DP in O((2/V)^3) or even O((2/V)^2) https://codeforces.me/contest/1543/submission/121629108
nevermind, got it
Is it preferable to avoid using accumulate to find sum of vector in C++,as in problem B using accumulate to
find the sum of vector, solution gets failed on pretest 2,but when I switch to find sum in usual way it get passed. Does anyone have any idea about this?
Yes, it's better to use things you can control and understand.
When you use accumulate, the accumulative variable takes the type of the last argument. So if you pass an int, it'll be an int and you'll have overflow.
Writing 0ll in place of 0 , in accumulate function would have worked as 0 is int and 0ll is long long int , and int gives overflow. Your code ACfied
121621126
Can anyone help me why I'm getting TLE ? And help me to optimize it
I have guess it's java, is'nt it? T-T
I used python and it barely passed with same logic and its intended logic too T-T
Yeah I guess so. Same happened to me, even though my algorithm is identical to Idea 2 in the tutorial.
ok so apparently buffered reader isn't fast enough, but System.in.read(); is. Check this guys solution for reference: 122226246. I copied his fasterScanner method and my solution also got accepted.
I really enjoyed problem D even though I lost a lot of time and points getting TLEs because of slow python IO (had to switch to stdIO). I'll know better next time.
Anyway thanks for the nice problems.
Is the adaptive grader on problem D badly designed? https://codeforces.me/contest/1543/submission/121656699 gets accepted even though it has
//if(r == 1) return;commented out.It is because the adaptive grader is designed such that any solution which passes will pass only after exhausting all $$$n$$$ queries. Read the note given about adaptive grader given in the editorial. In order to pass all initial passwords, you need atleast $$$n$$$ queries, because with one query, you can pass not more than one initial password. So, even though it seems that your correct code may guess the correct password in less than $$$n$$$ queries, the correct code will use $$$n$$$ query only. So, returning or not returning doesn't make any difference.
Yes, that's exactly the problem. The grader assumes that the best way to break people's solutions is by checking whether they are correct for all n possible starting passwords by always saving the "correct query" until the very end. In my opinion, having this grader for every single test case is bad design because it allows some incorrect solutions (like the one I posted) to pass. Ideally, there should have been at least one or two test cases that don't use this algorithm so that incorrect solutions like the one I posted fail.
A few words on this round. I will refrain from commenting on floating-point stuff (related to C) because basically everyone else has already done it. :)
Overall, I consider this a bad round, even though there have been worse.
On the other hand, the editorial is really well-written and understandable!
deleted.
There can be a much better solution to D2. In case of k = 2, number itself is kind of k-wise xor inverse. So, if we think in terms of k-wise xor inverse of a number it would be easier to understand that solution and come to the solution as well
How can we arrive to solution if we think in terms of k-wise xor inverse? The solution given in the editorial seems like a guess to me and then later proved with induction. Can you please tell me how to arrive at the solution by oneself?
Let xi,k be a number such that k-itwise xor of x and xi is 0. If x was password , y is the guess made then z is new password such that
If we take k-itwise xor with xi,k both side we get —
xi,k (xork) x (xork) z = y (xork) xi,k
z = y (xork) xi,k
Therefore new password is k-itwise xor of k-wise xor inverse of old password and guess.
I would like to state one property before we go on to solution —
(a xork b) i,k = ai,k (xork) bi,k
This can be simply proved if we think in terms of k-its
In mth guess we will guess the number supposing original number was m-1
So, the order is
password — x
guess — 0
new password(if guess wrong) — xi,k (xork) 0 = xi,k
password — xi,k (xork) 0
guess — 1i,k (xork) 0
new password(if guess wrong) — (xi,k)i,k (xork) 0 = x (xork) 0 = x
password — x
guess — 2
new password(if guess wrong) — xi,k (xork) 2
password — xi,k (xork) 2
guess — 3i,k (xork) 2
new password — (xi,k (xork) 2)i,k (xork) (3i,k (xork) 2)
= x (xork) 2i,k (xork) 3i,k (xork) 2
= x (xork) 3i,k
password — x (xork) 3i,k
guess — 4 (xork) 3i,k
So, we can simply see that ith guess is
if i is odd — (i-1) (xork) (i-2)i,k
if i is even — (i-1)i,k (xork) (i-2)
As I didn't have mathematical symbols, solutions look a litle complicated than it is.
Thanks a lot. But to be honest, it still seems like a guess to me. I think I should just leave the problem for now and get back to it after some time. Thanks again.
Everyone be complaining about messy problem statements but the truth is
You just haven't played NEED FOR SPEED: MOST WANTED.
Prob C brought to light my misconceptions of float operations. The NFS: MW references were a joy to read and recall, despite their irrelevancy. Thank you very much for this contest!
D1 is annoying, same algorithms but using Python will get TLE (maybe because output is so slow) really unfair.
I can't understand the brute force implementation of problem C , i can't understand the addition of 1 and then the recursive call
E(c,m,p,v)=1+c*E(c-v,m+v/2,p+v/2,v)+m*E(c+v/2,m-v,p+v/2,v). I have not included the extra if/else cases here. Just initialise the recursion with 1 and continue.I really still don't understand why plus 1. Can you explain a bit more?
In the definition of problem, the probability is about "count of all race until P is selected" So, select C or M means one more race. So +1
I have solved C using doubles, but I tried to solve it again by converting it to integers after multiplying it with scale as given in the editorial. However, I am getting overflow doing that. I have already defined
# define int long long.Can someone point out the error, please? My code
The reason of over flow is while returning the value from val function , you are returning no.>= 1e6 , which in more than 3 multiplication will lead to overflow .
Yeah, thanks. It worked. Moreover, I was initializing my answer with 1e6, it should have been 1e12. I had one more doubt, I have mentioned that in this comment.
For the first part of question E, you can find the inverse permutation s as follows.
Pick any vertex V and let s(V)=0. Then send the neighbors of V to the powers of 2.
In the standard n-cube, the distance of i to 0 is just the number of bits set in i. Moreover, the vertices which occur on some shortest path from i to 0 are precisely the submasks of i. In particular, if i is at a distance of >=2 to 0, then i is the bitwise or of its neighbors which are closer to 0.
To find the inverse permutation, we can proceed by doing a bfs after assigning the neighbors of V. When we reach vertex v, let s(v) be the bitwise or of s(w) as w ranges over the neighbors of v which have already been seen. (Here, we should note that two vertices at the same distance from 0 in the standard cube have at least 2 different bits, so are not neighbors. Thus a neighbor is closer to the staring vertex V if and only if it has already been seen).
This gives us the inverse permutation. To go back the original permutation, sort the list of i by s(i).
is this contest unrated ?
I want to ask the same question.
My rating hasn't changed, either.
I wish so. May the ratings be with us.
Could anyone tell me why my rating hasn't changed?
Problem E can be found in YouTube.
So is it unrated?
Probably not.These two things are not related.
Can you give some tips for questions like E. Others were relatively easy but I have never seen anything like E before and even after the contest its hard to understand. Any resources would be nice
Can somebody tell the time complexity of problem C in the simplest way?
UPD: GOT it.
btw I love the problem D1.
in question 3 it showed pretest passed(3) but later during system testing it showed TLE on testcase 2.How is it possible means why it then showed pretest passed???
oh i got it it was precesion error
Thankyou for this round, I messed up C for 1 hour due to precision errors but learned something in the process. D1 and D2 were interesting to me as well.
Nice round although wasn't able to solve C but got to learn new concept of precision Handling today
ans += (c/scale)*(1+expectedRaces(c-v,m+v/2,p+v/2,v));
I don't understand where the number 1 comes from in this expression
With c probability, you'll play 1 move, plus, the expected number of moves starting from new probabilities. That's why "1 + E(c-v, m+v/2, p+v/2, v)"
Can anybody explain their thought process for D1?
"n queries and n possible answer" made me think, why not check all the numbers one by one. But the only problem here is, every "possible answer" will change after each query. So why not keep track of queries.
We have to query 0 at first. all possible answers x will change to y, satisfying x^y=0. Using the properties of bitwise XOR, y = x^0 = x.
After the first query, "possible answers" haven't changed. But soon you'll find out that this isn't the case with other queries.
Next you query 1 as it is the next "possible answer". This will change all the numbers from x to y satisfying x^y=1 and thereby y = x^1.
The next step is the most important and interesting one. So listen carefully :p
Till now, we have queried 0 and 1. This would have caused all the possible answers y to change to y ^ 0^1 (y ^ 0 in the first step and y ^ 0^1 in the next). If you get this step, you are good to go and retry it yourselves.
Our next "possible answer" was 2 in the initial state. You've guessed right. It would have become 3 by now. So query 3.
Other "possible answers" y would have become y ^ 0^1^3. For example, if the initial answer was 3, it would have become 3 ^ 0^1^3 = 1.
But isn't it hard to keep track of these everytime? Don't worry. If you look carefully, in step 7, we queried 3 which we found out by 2 ^ 0^1. 3 = 0^1^2 implies 0^1^3 = 2 (This is the same 0^1^3 in Step 8). This way, you can just query 3^2 to check if the initial answer was 3.
Last step, 4 would have become 4 ^ 0^1^3^1 = 7 by now. This is just 4 ^ 3. Similar way, it continues
This was my thought process, pretty fucked up, ik .
So realizing that if x^z = y can be written as y^x = z seems to be a critical observation. How did you realize that ?
I knew that
x^x = 0and0^z = zfrom the truth table of bitwise xor operator.Hence,
x^z = y=>x ^ x^z = x ^ y=>(x^x) ^ z = x ^ y=>z = x^yYou are the real boss among all the people who comments, the problemsetters and the editorialist.
Just think about D2, then restrict the solution to $$$k=2$$$.
Is this the reason why you failed solving D1 during the contest? Solving the problem for $$$k=2$$$ and then trying to generalize the solution seems to be much more rewarding.
The logic is basically the same, the only difference when $$$k=2$$$ is that $$$i \oplus j = i \ominus j$$$.
Orz
It seems like the coloring part of E is touched on in this video. It's also a great watch, with a nice application of the problem.
The game mentioned in the video is also a nice, intuitive way to come up with the xor-based solution. Let's consider playing the coin game on a $$$n$$$-square board. As explained in the video, flipping exactly one coin corresponds to moving to an adjacent vertex in the (non-permuted) $$$n$$$-hypercube, with each bit corresponding to whether each coin is facing heads or tails. Let's color the vertices of the hypercube so that the state with the color $$$c$$$ corresponds to the key being under square $$$c$$$. Therefore, as we need to be able to communicate any value of $$$c$$$, we require that the set of colors of neighbors of any vertex must have all possible colors from $$$0$$$ to $$$n-1$$$, hence any solution to this coin game is equivalent to a desired painting of the $$$n$$$-hypercube.
Now, what's a simple solution to the coin game (when $$$n$$$ is a power of $$$2$$$)? Let's number each square from $$$0$$$ to $$$n-1$$$. Let's define some value $$$v$$$ calculated from the state of the board that we can change to any other value by flipping exactly one coin. Well, xor of numbers of all squares with heads works here because by flipping one coin in square $$$s$$$, we flip all bits in $$$v$$$ corresponding to mask of $$$s$$$. As we can choose any mask (due to $$$n$$$ being a power of 2), we can flip exactly one coin to change $$$v$$$ to any value between $$$0$$$ and $$$n-1$$$. Therefore, we can change the board state such that $$$v$$$ is equal to the square under which the key is located.
It is not difficult to see that this solution to the coin game corresponds to the coloring shown in the editorial.
Could you guys help me with TLE on D1 with java? https://codeforces.me/contest/1543/submission/121703927
can anyone explain in problem C(solution) we are adding V/2 which rounded down always. Will it not affect the answer?
They first scaled the input by $$$1e6$$$. Since the number of decimals is at most 4 it is therefore guaranteed to be divisible by 2, so there will not be any rounding error.
E.g. $$$0.1234$$$ is scaled to $$$123400$$$ which is divisible by 2.
If someone doesn't know anything about precision errors, why it happens and how to solve it, can refer to this article to get the basic idea.
The Answer to test case 0.4998 0.4998 0.0004 0.1666 should be 5.0307188293 instead of 5.05 Since v is 0.1 minimum so the game ends in max 20 turns(since you are taking atleast v/2 from the c + m collection). If you simulate the game till 20 turns for all possible CM combinations you get 5.0307188293. The approximation I see every where of comparing with 1e-9 is not accurate.
Ok this might be a dumb question but in
why the 1?
Read this comment.
In the editorial, the author JaySharma1048576 has used a scale of 1e6.
However, when I am using a scale of 1e6, it is giving WA on Test 8. Code-121732306
On the other hand, when I am increasing the scale, it's giving AC. Submissions-121733647 and 121733750
Can someone tell me please, what should be the minimum scale to avoid integer overflow, as using 1e6, would have given FST in Contest?
1e6 worked for me https://codeforces.me/contest/1543/submission/121735506
Your solution is almost same as the editorial solution, by which all the solutions are checked. I am asking the reason.
You should take
c = round(c1*xx)instead ofc = (c1*xx)in your code because0.1*1000000may be equal to99999.9999999..., again because of precision errors with floating point numbers. Typecasting it to int will give99999but it should be100000for which you should use theround()function. The scale of $$$10^6$$$ is completely fine in this problem because the inputs have $$$4$$$ decimal places at max.Oh, thanks a lot. Learnt a new thing today.
bruh i tried to do a O(d^2) sol for C
Sorry for posting this late, but can someone please explain why 1e-10 works in the below line for a solution to Problem C, but 1e-9 doesn't?
Shouldn't they both be working?
The submissions: 1e-9, 1e-10.
The coloring part of problem E was posed here: https://codeforces.me/blog/entry/52918
JaySharma1048576 Can you please share the code of adaptive checker for D1 & D2?
Hey can somebody explain the reasoning behind the following behaviour? I am converting the floating numbers to integers by multiplying them with a constant (like 10^5, 10^7 etc).
Can you please explain why this is happening particularly in this case? I get that recurring numbers (in binary representation) don't get stored exactly due to the recurring component but we would never end up in a recurring situation since 0.0001 would get divided at most once and become 0.00005. Hence the question about why 1e5 is not enough.
Is it the case that the constant multiplication of the dp terms like c * p * p *.... and so on is causing the error to seep in? How do we decide the constant to scale the floating numbers in that case short of just experimenting and seeing what works?
For this problem, if you see how the values may change during the whole process, you will notice that these values may get divided twice and not once (see this comment for more details). So, taking a scaling factor of $$$10^6$$$ or greater works here.
If you take a factor of $$$10^5$$$, then one of the values of $$$\frac{a}{2}$$$ may not be an integer. For example, take
(0.3000, 0.1000, 0.6000, 0.2001). After choosingC, the probabilities will become(0.0999, 0.20005, 0.70005, 0.2001). Now, if you chooseM, the probabilities will become(0.199925, Invalid, 0.800075, 0.2001). So you can see that the probability ofPbecame 6 decimal places.Oh yeah, completely missed that. Thanks! :)
However I still don't understand why 10^7 doesn't work without setprecision. Any why 10^6 fails with or without setprecision.
setprecision controls how many decimal places you want to print. By default, it is quite less and since the maximum error allowed is $$$10^{-6}$$$, you need to set it to something more than 6 decimal places.
Okay, that makes sense. face palm Thanks for taking the time to replying! :) Really liked the questions!
For anybody else who's wondering why won't 10^6 work with setprecision: try running
Why?
Disclaimer: I don't know much about how things work closer to the metal. Please let me know if I'm making a mistake somewhere.
Hi! Can somebody help me understand in sequences from solution at problem C like:
(1+expectedRaces(c-v,0,p+v,v))how that +1 helps in finding the right answer? I mean I understood the idea of calculating the answer and how that solution works, but that +1 scares me. I tried simulating on paper but with no results:(