danhnguyen0902's blog

K-TH QUERY
By danhnguyen0902, 11 years ago, In English

Given a sequence A of N pairwise-distinct integers. There are Q queries L R K, asking for the k-th element in the increasing-sorted subsequence A[L], A[L+1], ...., A[R-1], A[R]. The original sequence never changes.

  • 1 ≤ N, Q ≤ 10^5

  • |Ai| ≤ 10^9, 1 ≤ i ≤ N

  • 1 ≤ L ≤ R ≤ N

  • 1 ≤ K ≤ R-L+1

Example:

Input:

7 (N)

2 1 5 4 3 6 8 (sequence A)

4 (Q)

1 2 2 (L R K)

3 7 4

4 6 2

5 5 1

Output:

2

6

4

3

  • Vote: I like it
  • -2
  • Vote: I do not like it

Comments Comments (40)
| Write comment?
»
11 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

This problem exist on spoj MKTHNUM

here is my O((N+M) sqrt N) solution:

solution

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could someone explain me this solution please?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      LushoPlusPlus So the idea is to replace each element of the given array by it's compressed value [index of this element if we sort the whole array]. It's simply done in $$$O(n.log(n))$$$. Also, save the inverse mapping, i.e. $$$pos[compressed$$$ $$$value(a[i])] = i$$$.

      Now, we will use this array $$$pos[1..n]$$$ to answer queries $$$l,r,k$$$. How ? the first index $$$i$$$ such that $$$l \le pos[i] \le r$$$ will be the smallest compressed value in $$$a[l..r]$$$. Next index satisfying the inequality will be second smallest value and so on. We have to find the $$$k_{th}$$$ such index.

      Build partial frequencies of each element [and for each block]. Break $$$a[1..n]$$$ into $$$\sqrt n$$$ blocks. Iterate through blocks and in each, find number of elements satisfying the inequality use partial frequencies. The first block where number of elements $$$\ge k$$$, traverse it using brute force.

      → Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    kingofnumbers did you find a way to perform point updates as well in this problem?

    → Reply
»
11 years ago, # |
  Vote: I like it +1 Vote: I do not like it

O(M log^2 N) solution is here

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    could you explain your solution briefly ?

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it
      • Build merge sort tree
      • During traversal on merge sort tree, divide current interval from middle then if ask is there enough number at left one in O(logN) , if enough go left else right.
      • Maximum depth of traversal is O(log N) and each depth has O(log N) complexity.
      • Overall complexity is O(log^2 N) at each query.
      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        thanks.

        it's a nice usage of merge sort tree.

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I am not able to understand your solution can you tell a little more deep

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        but how can i sort the segments ?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Read merge-sort algorithm. It's pretty straightforward after you read that .

          → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    ikbal Nice solution, but it doesn' support point update though.

    How to solve for point updates?

    → Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

It can be solved in O((N + M)log(N)) using persistent segment trees: let's replace all numbers with numbers in range 1..N, and then for each prefix we can callculate a tree, such that nth position in a tree is a number of occurences of n in that prefix. Imagine a segment tree made by the same rule for subsegment [L, R]. each vertex of such a tree is a difference of a corresponding vertex in tree for [1..r] and such a vertex in tree for [1..l-1]. So we can implicitly acess vertex v of such tree simply by subtracting corresponding vertexes. Having a tree for [L..R] let us find an onswer quickly by simple recursive procedure in this tree. I'm sorry for explanation that's not very clear, but the solution is here

→ Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I got the idea and it's interesting , but I am not able to understand how you create a tree for each prefix (total n trees) without having complexity O(N^2) , I also couldn't understand the code can you give quick explanation for each variable, array and function in this code

    thanks.

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +16 Vote: I do not like it

      I use persistent segment tree to create n trees in O(nlogn) time. That means, that I do not modify any tree node. Instead I create a new node every time. This way I can always use any old version of a tree. Each update operation on a segment tree takes O(logN) time, O(logN) additional memory and produces a root of new segment tree, that reuses some parts of an old one. Anytime a node would be modified in a simple segment tree a new node with another value should be created in a persistent one. A tree for [1...k] is just tree for [1..k-1] where some element with a value x is replaced to some element with value (x + 1).

      I slightly modified the code for it to fit to SPOJ version of a problem, though I didn't change the point. This version gets AC on SPOJ.

      About functions:

      allocate(x = 1) allocates exactly x segment tree nodes from a constant array. A pointer to the first of them is returned

      update(v, vl, vr, x) increases by one the value of x node in subtree tree rooted in v, where [vl; vr-1] is segment corresponding to that subtree. In all outer functions it is used that way: update(v, 0, maxn, x). That functions returns the root of a new subtree leaving the original untouched.

      find_nth(u, v, vl, vr, nth) finds an nth element on a tree that is difference of v and u. vl and vr are the boundaries of a subsegment this function is operating on now. It returns a pair of a current result and a flag — should we continue searchin to the right, or not. That flag is not used outside of that function

      array — input array

      coords — sorted input array. It is used to replace numbers in range [-10^9; 10^9] with numbers in range [0...n-1]

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Thanks a lot I learnt about persistent data structures and understood it.

        but can the persistent segment tree support operation for editing an element in array in addition to finding k-th number? I mean to can it solve this problem:

        we have array with length N and M operations with two types the first is finding kth-number in some interval and the second editing a number in the array

        I as know if I want to edit an element in array then I need to edit it in at most N trees

        → Reply
        • »
          »
          »
          »
          »
          10 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Did you get the answer for this question ? If yes, can you please tell how can we do the problem if update operations were also present ?

          → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it -8 Vote: I do not like it

            Looks like it is possible only with merge sort tree and .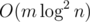

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              5 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              adamant Can you explain how merge sort tree supports point update in this problem?

              → Reply
          • »
            »
            »
            »
            »
            »
            10 years ago, # ^ |
              Vote: I like it +1 Vote: I do not like it

            However persistent segment tree let you make another interesting modification — you can push new elements to the end of array.

            → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            There's a method which support point update. :)

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              3 years ago, # ^ |
                Vote: I like it -24 Vote: I do not like it

              How? Each "version" of the persistent seg tree corresponds to inserting an index in the array.

              So a point update in the array corresponds to modifying a previous "version" of the PST, which means you have to recalculate all future "version"s as they possibly could depend on this update

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                3 years ago, # ^ |
                  Vote: I like it -8 Vote: I do not like it

                You can use a fenwick tree to maintain those prefix "persistant" segment tree.

                → Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Great problem! I really enjoyed learning about persistent segment trees, thinking an implementation and then coding it.

New knowledge is always welcome :)

I got AC with that idea. Here is the code -> Code

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think your solution is O(N log^2 N) while it should be O(N log N) if you are using persistent segment trees

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 3   Vote: I like it +1 Vote: I do not like it

      Yes, it's O(M log^2 N)... I sort the array, and then create N segment trees (only the first one is allocated entirely, the other ones only allocate the differences (log(N) nodes)), that store how many elements in a certain range appear in that tree. The first tree will have 1 element in total, the second one will have 2, ..., the last one will have a total of N elements.

      After that, I search the trees using binary search until I find the first tree that has K nodes in the range L..R.

      How can I make it O(M log N) ????

      → Reply
      • »
        »
        »
        »
        11 years ago, # ^ |
        ← Rev. 2   Vote: I like it +1 Vote: I do not like it

        You don't need the binary search , you can find the k-th number in range L .. R using idea very similar to the idea of finding k-th node in a BST see the code of pshevchuk here

        → Reply
        • »
          »
          »
          »
          »
          11 years ago, # ^ |
            Vote: I like it +1 Vote: I do not like it

          I think I get it. The problem is that instead of working on the numbers themselves, my segment trees work based on indexes.

          I'll recode it later and work on the numbers (after compressing them), and then make a query that works on trees R and L-1 at the same time.

          → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Hey, Hasan.
          How can the code be edited for repeated array elements?
          Please help.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Are all integers in your input pairwise-distinct?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              No they weren't. But now I realized that for this code the elements were pairwise distinct. Can you help me out if the elements aren't pairwise distinct? It would be very helpful. Thank you.

              → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Good. I recoded it and now the solution is O((M+N) log N).

      Here is the updated solution -> Code

      → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    What is the use of passing 'n' as an argument to your insert() function? You don't use it anywhere inside it.

    → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Here are two practice problems that can be solved using the same idea... - http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4273 - http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=2716

→ Reply
»
9 years ago, # |
  Vote: I like it -9 Vote: I do not like it

Here is my solution http://ideone.com/iNSQ1M with O(M log^2 N) aproach. But i am getting TLE. Can anyone help?

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it -11 Vote: I do not like it

spoj problem : http://www.spoj.com/problems/MKTHNUM/ i got AC using merge sort tree...here is my soln https://ideone.com/fork/CQI7qe

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anybody explain how to do this question if elements in array can repeat also?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There's another method to solve this problem, which can support editing. (point)

Using segment tree and build a treap for each node on the tree. When we update a[i]'s value, we can go From root to leaves and update the treap which the node was on the path. One update is O(logn).

to finding kth-element, we can use Binary Search.

If we supposed that x is the answer: We all know that any range [L...R] can split into <=logn nodes on the segment tree. So we can find these nodes and using treap to find the rank of x in [L...R].

And we can use the result to change the answer.

(If anyone already explains about it, please ignore me)

→ Reply