Does anybody know if there will be a tutorial for abbyy finals? If there is not going to be a tutorial soon, please give me some hints for tasks A,B,C. THANKS A LOT!!!
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 26.11.2024 16:25:37 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











A is more or less greedy: If you have a pair of equally appealing trees at positions i and j and you want to keep them as the outermost trees, you need to delete all trees at positions < i and > j. Also, you remove all the trees in between that have a negative appeal. The total remaining sum of appeals will be f(i, j) = psum[j - 1] - psum[i] + a[i] + a[j] where psum[k] is the sum of positive appeals in the range 0..k (it can be precomputed upfront). This is the maximum possible appeal if you decide to use i and j as the outermost trees.
Now how to find the pair (i, j) that maximizes f(i, j)? We can enumerate j and always use the leftmost i with a[i] = a[j]. Why? Because f(i, j) = 2·a[j] + psum[j - 1] - psum[i], so f is monotonically decreasing when i increases. We can use a
map<int,int> posso that pos[x] is the leftmost i such that a[i] = x. Then we can just iterate over the array a, checking pos[a[j]] for every position j and then updating pos with the value a[j]. The maximum over all iterations is the total maximum.Run time: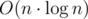 or expected O(n) with a hash table. Code: 4099310
or expected O(n) with a hash table. Code: 4099310
B: Let pos[i] be the position of the beaver i in the current permutation. For x > 1, let x[i] = 1 if pos[i] < pos[i - 1] and x[i] = 0 otherwise. Let a(l, r) be the result of a query of type 1. Intuitively, we get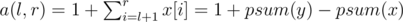 , where psum(k) is the prefix sum of x up to and including index k. We can use a binary indexed tree to store x, so that we can compute psum(k) fast.
, where psum(k) is the prefix sum of x up to and including index k. We can use a binary indexed tree to store x, so that we can compute psum(k) fast.
Now for every swap, at most 4 different values of x can change, so we only need a constant number of updates of our data structure per swap. This results in a total complexity of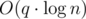 .
.
Code: 4099288
C: I only solved C1, using DP with a straightforward recurrence: f(0) = 0 and f(x) = minD(x)f(x - d) (where D(x) is the set of digits of x)
Code: 4099317
B: When you change values of x, what do you do to the index tree?
You "set" the value. I just saved the array
xexplicitely and added 1 or -1 if a value changed (see theupdatefunction in my code).The editorial is published now: here, but it's too short. I'd say the niklasb's explanations of A and B are much better than that.