Автор: AlexSkidanov
Если несколько прямоугольников образуют квадрат N × N, то следующие два условия обязательно выплняются:
1) Суммарная площадь прямоугольников равна N × N.
2) Разница между правой границей самого правого прямоугольника и левой границей самого левого прямоугольника ровно N. Аналогично для нижней и верхней границы.
Легко показать, что эти условия являются также и достаточными.
Автор: nika
Пусть прошло D раундов на выбывание, и круговой раунд с M командами.
Тогда общее количество сыгранных игр: 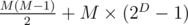
Мы хотим, чтобы 
Это уравнение с двумя неизвестными, чтобы его решить, можно зафиксировать значение одной из них, и найти значение другой. Мы не можем перебрать все значения для M, так как M может достигать 10^9. Однако, мы можем перебрать все значения D, так как количество игр растет экспоненциально с ростом D -- поэтому D может принять значения только в интервале 0 ≤ D ≤ 62.
Когда D зафиксировано, остается решить следующее уравнение: 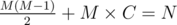
Так как левая часть уравнения возрастает, M можно найти двоичным поиском.
Автор: AlexSkidanov
Первая часть задачи -- найти минимум для каждого монстра. Чтобы это сделать, мы будем использовать алгоритм Дейкстры. Изначально минимум не известен ни для одного монстра. Для каждого превращения будем поддерживать величину, указывающую на количество монстров, которые это превращение создает, для которых минимум еще не известен (назовем его ki для i-ого превращения). Сначала рассмотрим каждое превращение, которое создает только бриллианты (то есть для которого ki = 0), и скажем, что это количество бриллиантов -- это временный минимум для монстра, которому принадлежит превращение (если у монстра есть более одного превращения в бриллианты, надо взять то, которое создает минимальное количество бриллиантов). Затем возьмем монстра с минимальным временным минимумом. Для этого монстра временный минимум является финальным минимумом. Это можно доказать используя подход, похожий на подход к доказательству алгоритма Дейкстры. Так как для этого монстра минимум известен, уменьшим ki для каждого превращения, которое производит этого монстра. Если для какого-то превращения ki стало равно нулю, обновим временный минимум для монстра, которому принадлежит это преврещение суммой минимумов по всем монстрам, которых это превращение производит, и количества бриллиантов, которые это превращение производит. Затем, среди всех монстров, для которых финальный минимум еще не известен, но известен временный, выберем того, для которого временный минимум минимален, и повторим процесс.
Когда монстров, для которых есть временный минимум, но нет финального, не осталось, все монстры, для которых минимум не нашелся, будут иметь - 1 - 1 в качестве ответа. Для остальных монстров мы знаем минимум, но не знаем максимум.
Вторая часть решения -- избавиться от превращений, выполнив которые мы никогда не сможем избавиться от всех монстров. Легко показать, что такими превращениями являются те, в результате которых появляется хотя бы один монстр, для которого минимум равен - 1. Уберем все такие превращения из набора превращений.
После этого найти максимумы очень легко. Начиная из каждого монстра, для которого максимум еще не известен, будем обходить монстров обходом в глубину. Для данного монстра, рассмотрим все превращения. Для конкретного превращения, для каждого монстра, который появляется в результате этого превращения, вызовем DFS чтобы найти максимум для этого монстра, просуммируем эти величины, прибавим количество бриллиантов, которые это превращение создает, и улучшим известный максимум для монстра, которому принадлежит это правило, полученной величиной. Если мы в какой-то момент времени попадаем в ситуацию, когда DFS вызван для монстра, для которого уже есть вызов DFS на стеке, это значит, что этот монстр может превратиться сам в себя (непосредственно или через других монстров) и ненулевое количество бриллиантов (по этой причине в условии оговаривается, что каждое превращение генерирует хотя бы один бриллиант), поэтому ответ для такого монстра -2. Если, обрабатывая одно из превращений, мы обнаружили, что в результате применения превращения появится монстр, для которого максимум равен -2, мы можем сразу назначить максимум для текущего монстра в -2 и выйти из DFS.
В качестве упражнения подумайте, как решить эту же задачу, если не гарантируется, что каждое превращение содержит хотя бы один бриллиант.
Автор: dolphinigle
Для простоты допустим, что над самой первой строкой и под самой последней строкой есть по дополнительной строке с морем.
Раздвоим поверхность цилиндра, добавив его справа к самому себе (при этом левый столбец раздвоенного моря по прежднему смежен с правым столбцом). Каждое превращение будем осуществлять в обеих половинах. Утверждается, что торгового маршрута не существует тогда и только тогда, когда для некоторой превращенной ячейки она достижима из своей копии по превращенным ячейкам (две превращенных ячейки смежны, если у них есть хотя бы одна общая точка, не обязательно общая сторона).
Доказать тот факт, что это услвоие достаточно, очень легко. Путь между ячейкой и ее копией разбивает море на северную и южную часть, и представляет из себя барьер между этими половинами, который ни один торговый маршрут не может пересечь.
Докажем необходимость условия. Пусть ни для какой превращенной ячейки ее копия не достижима по превращенным ячейкам. Тогда возьмем все ячейки, содержащие море, прилегающие к верхней границе, и найдем все достижимые из них ячейки с морем (две ячейки с морем смежны, если у них есть общая сторона). Пусть ни одна ячейка с морем, достижимая таким образом, не прилегает к нижней границе. Тогда возьмем самую нижнюю достижимую ячейку с морем (любую если их несколько), и начнем двигаться вправо вдоль морских ячеек, по превращенным ячейкам. Легко показать, что двигаясь по превращенным ячейкам, имеющим хотя бы одну общую точку, вдоль границы моря, мы опишем круг вокруг цилиндра и вернемся в ячейку, с который мы начали, что противоречит тому, что ни для какой превращенной ячейки ее копия не достижима из нее.
Дальше будем решать задачу моделируя запросы. Будем поддерживать компоненты связности превращенных ячеек используя систему непересекающихся множеств. Каждый раз, когда ячейка превращается, убедимся, что эта ячейка и ее копия не содержат соседей, принадлежащих одной компоненте связности. Если такие соседи есть, то после превращение этой ячейки, она и ее копия окажутся в одной компоненте связности, тем самым не оставив ни одного торгового маршрута. Если таких соседей нет, то превращаем ячейку, и объединяем все компоненты связности, прилегающие к ней, затем превращаем копию ячейки, и объединяем все компоненты связности, прилегающие к ней.
В этой задаче стоит отдельно рассмотреть случай, когда столбец только один (тогда ни одно превращение нельзя осуществить), и когда столбцов два (тогда у каждой ячейки только 5 соседей, а не восемь, что может привести к ошибкам в некоторых реализациях).
Автор: nika
В этом разборе все числа подрузмеваются по модулю N. Если в разборе встречается число 10, имеется ввиду 10 по модулю N.
В задаче нас просят найти гамильтонов цикл в графе. Для каждой вершины гамильтонова цикла через bef(X) будем обозначать предыдущую вершину в цикле а через aft(X) -- следующую.
Сначала покажем, что ответ -1 для любого нечетного N.
Рассмотрим вершину 0. Для любой вершины H, ведущей в 0, выполняются два условия:
2H = 0
2H + 1 = 0
Первому условию удовлетворяет только H = 0. Второму условию удовлетворяет только floor(N / 2).
Иными словами, pre[0] = floor(N/2), и aft[floor(N/2)] = 0
Теперь рассмотрим вершину N - 1. В нее ведут вершины, для которых верно
2H = N - 1
2H + 1 = N - 1
Второе условие выполняется только при H = N - 1. Первое условие выполняется только при H = floor(N / 2)
Иными словами, aft[floor(N/2)] равен N - 1. Это противоречит тому, что aft[floor(N/2)] должен быть 0.
Тем самым доказано, что N четно. Этот случай намного интереснее.
Рассмотрим вершину X. Из нее есть ребра в 2X и 2X + 1. Рассмотрим вершину X + N / 2. Из нее есть ребра в.... 2X + N и 2X + 1 + N. ...что по модулю N равно 2X и 2X + 1.
Значит, для вершин X и X + N / 2 множество исходящий ребер идентично.
Легко показать, что для каждой вершины X есть ровно два входящий ребра. Это следует из того, что в вершину X ребра идут только из вершин таких, что
2H = X
2H + 1 = X
по модулю N, и каждое из этих уравнений имеет ровно одно решение.
Факт, что каждая вершина имеет ровно два входящий ребра, вместе с фактом что X и X + N / 2 имеют одинаковое множество исходящий ребер, дает нам понять, что в вершины 2X и 2X + 1 есть ребра только из X и X + N / 2.
Иными словами, если мы решили взять ребро из X в 2X в гамильтонов цикл, мы обязаны взять ребро из X + N / 2 в 2X + 1 в цикл тоже (и наоборот).
Теперь, следуя правилу выше, для вершин X, X + N / 2 возьмем любые два из четырех ребер в 2X, 2X + 1. В итоге мы возьмем ровно N ребер, которые образуют некоторое количество простых циклов. Можем ли мы легко объединить? Оказывается, что в силу особенностей этих циклов, мы можем это сделать.
Утверждение: если есть два или более цикла, то есть вершина X такая, что X и X + N / 2 принадлежат разным циклам.
Доказательство: Пусть это не так. Покажем, что в этом случае есть только один цикл. Так как вершины X и X + N / 2 принадлежат одному циклу, они должны быть в одном цикле с 2X и 2X + 1. Так как X и 2X и 2X + 1 все принадлежат одному циклу, легко показать, что из любой вершины X можно попасть в любую другую вершину Y (доказательство этого остается в качестве упражнения). Теперь, расммотрим X такое, что X и X + N / 2 принадлежат разным циклам. Пусть из вершины X сейчас выбрано ребро в 2X + A, а из вершины X + N / 2 -- в 2X + B (A + B = 1). Поменяем их местрами -- пойдем из X в 2X + B и из X + N / 2 в 2X + A. Это соединит два цикла в один -- идея очень похожа на идею построения эйлерова цикла. После каждой такой операции количество циклов уменьшается на один, и в итоге останется только один цикл.
Осталось понять, как это сделать за O(N). Примером решения может быть DFS из вершины 0. Для каждой вершины X:
если мы в ней уже были, возвращаемся из DFS
если X + N / 2 была посещена, идем либо в 2X либо в 2X + 1 рекурсивно, в зависимсти от того, куда сейчас ведет ребро, выбранное для X + N / 2 (пойдем в вершину, в которую то ребро не ведет)
иначе, идем рекурсивно в 2X. Затем проверяем, смогли ли мы посетить в рекурсии X + N / 2. Если нет, значит они принадлежат разным циклам. Соединим их, и рекурсивно спустимся в 2X + 1.











About program E:
Actually, as far as I understand, that's exactly the search for Eulerian cycle in a graph on N/2 vertices. Let's put numbers 2i and 2i + 1 in one class, and draw an edge from i-th class to j-th class if there is an edge between their vertices in original graph. Then the edges go from class i to classes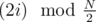 and
and 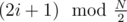 — just like in the original graph but with N replaced by
— just like in the original graph but with N replaced by 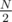 ! Now if we're in a vertex 2i of original graph, then we can leave it only by one edge in the new graph, because vertices 4i and 4i + 1 belong to the same class. So if we visited both vertices 2i and 2i + 1 in original graph, it means that we visited the vertex i in the new graph twice, and exited it by 2 different edges. That proves that the corresponding path in the new graph is Eulerian cycle and gives an algorithm to recover the original cycle from this Eulerian one.
! Now if we're in a vertex 2i of original graph, then we can leave it only by one edge in the new graph, because vertices 4i and 4i + 1 belong to the same class. So if we visited both vertices 2i and 2i + 1 in original graph, it means that we visited the vertex i in the new graph twice, and exited it by 2 different edges. That proves that the corresponding path in the new graph is Eulerian cycle and gives an algorithm to recover the original cycle from this Eulerian one.
The problem C has interesting interpretation. We have a context-free grammar (robots are nonterminals and diamonds are terminals). And the questions of the problem are to find lengths of the shortest/longest strings that can be produced from each nonterminal.
Is that origin problem formulation?
P.S. Code in grammar terms: http://codeforces.me/contest/325/submission/4067816
Yes, it is the origin of the problem. I was using it to optimize a CFG parser in one of my projects, so that it doesn't even try to parse a string, if its length is outside of [min, max] boundaries.
In B, I solved (M*(M-1))/2 + M*C = N, as a quadratic equation in M, rather than using binary search on M, but i got WA. I did not use BigInt. Is it due to overflow issues?
I did the same, but using BigIntegers and only integer numbers. Also got WA on pretest 5
I was also getting WA on 5, but that was an implementation error. Now getting WA on 38.
True, I also had implementation error, now AC — http://codeforces.me/contest/325/submission/4068404
Thanks, that means my WA is due to overflow only.
each of those two equations have exactly one solution.Actually one of them has no solutions and the other one has two.
Since
Nis even then parity ofXmakes sense moduloN.So if, e.g.,
Xis even, then2 H + 1 = X (mod N)has no solutions,while
2 H = X (mod N)has two —X/2and(X+N)/2.Thanks for problem D, it is really nice. The second part (when we note that the cut is an 8-neigours grid cycle) can be also solved like 196B - Infinite Maze.