I’ll present here the O(N ^ 3) algorithm, which is enough to solve this task. Then, for those interested, I’ll show a method to achieve O(N) complexity.
O(N ^ 3) method: The first thing to observe is that constrains are slow enough to allow a brute force algorithm. Using brute force, I can calculate for each possible single move the number of 1s resulting after applying it and take maximum. For consider each move, I can just generate with 2 FOR loops all indices i, j such as i <= j. So far we have O(N ^ 2) complexity. Suppose I have now 2 fixed vaIues i and j. I need to calculate variable cnt (initially 0) representing the number of ones if I do the move. For do this, I choose another indice k to go in a[] array (taking O(N) time, making the total of O(N ^ 3) complexity). We have two cases: either k is in range [i, j] (this means i <= k AND k <= j) or not (if that condition is not met). If it’s in range, then it gets flipped, so we add to count variable 1 – a[k] (observe that it makes 0 to 1 and 1 to 0). If it’s not in range, we simply add to cnt variable a[k]. The answer is maximum of all cnt obtained.
O(N) method: For achieve this complexity, we need to make an observation. Suppose I flip an interval (it does not matter what interval, it can be any interval). Also suppose that S is the number of ones before flipiing it. What happens? Every time I flip a 0 value, S increases by 1 (I get a new 1 value). Every time I flip a 1 value, S decreases by 1 (I loose a 1 value). What would be the “gain” from a flip? I consider winning “+1” when I get a 0 value and “-1” when I get a 1 value. The “gain” would be simply a sum of +1 and -1. This gives us idea to make another vector b[]. B[i] is 1 if A[i] is 0 and B[i] is -1 if A[i] is 1. We want to maximize S + gain_after_one_move sum. As S is constant, I want to maximize gain_after_one_move. In other words, I want to find a subsequence in b[] which gives the maximal sum. If I flip it, I get maximal number of 1s too. This can be founded trivially in O(N ^ 2). How to get O(N)? A relative experienced programmer in dynamic programming will immediately recognize it as a classical problem “subsequence of maximal sum”. If you never heard about it, come back to this approach after you learn it.
We’ll present two different solutions for this task.
Solution 1. What if we solve a more general task? What if each hungry number from the solution isn’t allowed to be divided by any number smaller than it (except 1, which is divides every natural number). If this more general condition would be met, then the “hungry” condition would be met, too (as a[i] won’t be divided by a number smaller than it (except 1), it won’t be divided by a[j], too, with j < i, assuming that a[j] is different from 1). Now how to find numbers for this more general condition? We can rephrase it as: each number from more general condition has 2 divisors: 1 and itself. So if we print N numbers with 2 divisors in increasing order, that would be a good solution. As you probably know, numbers with 2 divisors are called “prime numbers”. The task reduces to finding first N prime numbers. This can be done via brute force, or via Sieve of Eratosthenes (however, not necessarily to get an AC solution).
Solution 2. Suppose we are given the number N. We can observe that for big enough consecutive numbers, the array is always hungry. For example, we can print 3 * N + 0, 3 * N + 1, 3 * N + 2, …, 3 * N + (N – 1). Magic, isn’t it? Why does it work now? Pick an arbitrary a[i]. The solution would be bad if one of numbers 2 * a[i], 3 * a[i], 4 * a[i] and so on would be in a[] array. However, it will never happen. The smallest multiple from that ones will be 2 * 3 * N = 6 * N. There is not possible to obtain a smallest multiple than that one. On the other hand, the biggest number from a[] array would be 3 * N + N – 1 = 4 * N — 1. Since smallest multiple is bigger than biggest term of the array, it (and of course other multiples bigger than it) will never exist in a[] array. So the above solution is correct also.
Property: A number is divisible by 5 if and only if its last digit is either 0 or 5.
A first solution: Suppose you’re given a plate S, not so big, so we can iterate all its elements. Can we get the answer? I build a new array sol[]. In explanation, both S and sol will be 1-based. Denote N = size of S. Also, denote sol[i] = the number of ways to delete digits from plate S such as we obtain a magic number which has the last digit on position i. The answer is sol[1] + sol[2] + … + sol[N]. Let’s focus now on calculating sol[i]. If S[i] (digit of the plate corresponding to ith position) is different than 0 or 5, then sol[i] is 0 (see “property”). Otherwise we have to ask ourself: in how many ways I can delete digits in “left” and in “right” of position i. In the “right”, we have only one way: delete all digits (if one digit from right still stands, then the number isn’t ending at position i). Now in the “left”: there are digits on positions 1, 2, …, i – 1. We can either delete a digit or keep it – anyhow he’d do we still get a magic number. So on position 1 I have 2 ways (delete or keep it), on position 2 I have also 2 ways, …, on position i – 1 I have also 2 ways. Next, we apply what mathematics call “rule of product” and we get 2 * 2 * 2 … * 2 (i – 1 times) = 2 ^ (i – 1). Applying “rule of product” on both “left” and “right” I get 2 ^ (i – 1) * 1 = 2 ^ (i – 1). To sum it up: If S[i] is 0 or 5 we add to the answer 2 ^ (i – 1). Otherwise, we add nothing. The only problem remained for this simple version is how we calculate A ^ B modulo one number. This is a well known problem as well, called “Exponentiation by squaring”.
Coming back to our problem: So what’s different in our problem? It’s the fact that we can’t iterate all elements of plate. However, we can use “concatenation” property. We know that if an element is a position i in the first copy, it will also be on positions i + n, i + 2 * n, i + 3 * n, …, i + (k – 1) * n (we don’t call here about trivial case when k = 1). What if iterate only one copy and calculate for all K copies. If in the first copy, at the position i is either 0 or 5, we have to calculate the sum 2 ^ i + 2 ^ (i + n) + 2 ^ (i + 2 * n) + … + 2 ^ (i + (k – 1) * n). By now on, in calculus I'll denote i as i — 1 (it's a simple mathematical substitution). A first idea would be just to iterate each term and calculate it with exponentiation by squaring. However, it takes in the worst case the same complexity as iterating all plate. We need to find something smarter.
2 ^ i + 2 ^ (i + n) + 2 ^ (i + 2 * n) + … + 2 ^ (i + (k – 1) * n) =
= 2 ^ i * 1 + 2 ^ i * 2 ^ n + 2 ^ i * 2 ^ (2 * n) + … + 2 ^ i * 2 ^ ((k – 1) * N) =
= 2 ^ i * (2 ^ 0 + 2 ^ n + 2 ^ (2 * n) + … + 2 ^ ((k – 1) * n)
We reduced the problem to calculate sum S = 2 ^ 0 + 2 ^ n + 2 ^ (2 * n) + … + 2 ^ (X * n).
What’s the value of 2 ^ n * S ? It is 2 ^ n + 2 ^ (2 * n) + 2 ^ (3 * n) + … + 2 ^ ((X + 1) * n). And what you get by making 2 ^ n * S – S ?
2 ^ n * S – S = 2 ^ ((X + 1) * n) – 1
S * (2 ^ n – 1) = 2 ^ ((X + 1) * n) – 1
S = (2 ^ ((X + 1) * n) – 1) / (2 ^ n – 1).
We can calculate both 2 ^ i and S with exponentiation by squaring and the problem is done. For "/" operator, we can use multiplicative inverse (you can read about that and about Fermat Little's theorem, taking care that 10^9 + 7 is a prime number). The time complexity is O(N * logK). Note: that kind of reduction of powers is called “power series” in math.
Alternative solution: For this alternative solution, we don't need to use any special properties of 5. In fact, we can replace 5 by any integer p and still have the same solution. So for now, I shall write p in place of 5.
This suggests a dynamic programming solution: denote dp(x,y) be the number of ways of deleting some digits in the first x digits to form a number that has remainder y (modulo p). For simplicity, we accept “empty” plate be a number that is divisible by p. Writing the DP formula is not difficult. We start with dp(0,0) = 1, and suppose we already have the value dp(x,y). We shall use dp(x,y) to update for dp(x + 1,*), which has two possible cases: either keeping the (x + 1)-th digit or by deleting it. I won't go into much detail here. The answer is therefore dp(N,0).
Clearly, applying this DP directly would time out. For a better algorithm, we resort on the periodicity of the actual plate. The key idea is that, we imagine each digit in the plate as a linear transformation from (x0, x1, .., x(p – 1)) to (y0, y1, y(p-1)). Obviously, (x0, x1, .., x(p — 1)) corresponds to some dp(i, 0), dp(i, 1) .. dp(i, p — 1) and (y0, y1, y(p-1)) corresponds to some (dp(i + 1, 0)), dp((i + 1), 1), ..., dp(i + 1, p — 1) .So we can write X * M(d) = Y, where X and Y are vectors of length p, and M(d) is the matrix of size p * p representing digit d (note that M(d) is independent from X and Y). By multiplying all |a|.K such matrices together, we obtain a transformation from (1, 0, 0, .., 0) to (T0, T1, .., T(p – 1)) where T0 is actually our answer (including the empty plate).
What's the difference? We can group the matrices in groups of length |a|, and lift to the exponent K. That leads to an algorithm with time complexity O(p^3(|a| + log K)), which could be risky. To improve, we should go back to our original DP function and observe that it is actually a linear transformation from (1, 0, 0, .., 0) to (R0, R1, …, R(p – 1)), if we restrict ourselves in the first fragment of length |a|. So instead of multiplying |a| matrices together, we can run DP p times with initial conditions (0, 0, .., 0, 1, 0, .., 0) to obtain the matrix transformation. The overall time complexity becomes O(|a| * p^2 + p^3 log K) .
In case you want to try some examples on your own, you may play this game, which is the origin of this problem: http://en.wikipedia.org/wiki/Tower_Bloxx
Now back to the analysis :)
The restriction given in the problem poses you to think of building as many Red Towers as possible, and fill the rest with Blue Towers (since there is no profit of letting cells empty, such cells can be filled by Blue Towers). Also, it's quite obvious to see that each connected component (containing empty cells only) is independent from each other, so we shall iterate the component one by one. Denote the current component be S.
Lemma 1 is impossible to build S so that it contains all Red Towers only.
Proof Suppose there exists such a way. Look up the last cell that is built (denote by x). Clearly x is a Red Tower, so at the moment it is built, x must be adjacent to a cell than contains a Blue Tower. However, it's obvious that there's no such cell (if there is, it must belong to S, which is impossible).
As it's impossible to have all Red Towers, it's natural to look up at the next best solution: the one with exactly one Blue Tower, and among them, we need to find the least lexicographic solution. Fortunately, we can prove that such a configuration is always possible. Such proof is quite tricky, indeed:
Lemma 2 Pick any cell b in S. It is possible to build a configuration that has all but b be Red Towers, and b is a Blue Tower.
Proof Construct a graph whose vertices correspond to the cells of S, and the edges correspond to cells that are adjacent. Since S is connected, it is possible to build a tree that spans to all vertices of S. Pick b as the root and do the following:
- Build all cells of S blue
- Move from the leaf to the root. At each cell (except the root), destroy the Blue Tower and rebuild with the Red Tower. To be precise, u can be destroyed (and rebuilt) if all vertices in the subtree rooted at u have already been rebuilt.
How can it be the valid solution? Take any vertex u which is about to be rebuilt. Clearly u is not b, and u has its parent to be blue, so the condition for rebuilding can be met. When the building is completed, only b remains intact, while others have been transformed into Red Towers.
So we get the following algorithm: do a BFS / DFS search to find connected components. Then, apply Lemma 2 to build a valid configuration.
Usually when dealing with complicated problems, a good idea is to solve them for small cases. Let’s try this here.
First case: K = 0. The answer is obviously N! (each permutation of p1, p2, …, pn would be good).
Next case: K = 1. The answer of this one is N! – |L1|. By L1 I denote all routes for which a prefix sum is equal to first lucky number. Obviously, if from all routes I exclude the wrong ones, I get my answer. If we can find an algorithm to provide |L1| in good time, then problem is solved for K = 1.
We can just try all N! permutations. Despite this method is simple, it has complexity O(N!), too much for the constraints.
Suppose we’ve founded a set of positions p1, p2, .., pk such as a[p1] + a[p2] + ..+ a[pk] = U1 (first unlucky number). How many permutations can we make? The first k positions need to be p1, p2, .., pk, but in any order. Hence we get k! . The not used positions can also appeared in any order, starting from k + 1 position. As they are n – k, we can permute them in (n – k)! ways. Hence, the answer is k! * (n – k)! Instead of permuting {1, 2, .., n}, now we need to find subsets of it. Hence, the running time becomes O(2^n). This is still too much.
Meet in the middle. We make all subsets for first half of positions (from 1 to N / 2) and them for second half (from N / 2 + 1 to N). For each subset we keep 2 information: (sum, cnt) representing that there is a subset of sum “sum” containing “cnt” elements. For each (X, Y) from left we iterate in the right. After choosing one element from the left and one from the right we just “split” them. To split 2 states (A, B) and (C, D), the new state becomes (A + C, B + D). But we know that A + C = U1. This comes us to the idea: for each (X, Y) in the left, I check (U1 – X, 1), (U1 – X, 2), … , (U1 – X, K) from the right. For each of them, the answer would be (Y + K)! * (N – Y – K)! . I can store (using any data structure that allows this operations, I suggest a hash) how(C, D) = how many times does state (C, D) appear in the right. So, for a state (A, B) the answer becomes a sum of how(U1 — A, K) * (B + K)! * (N — B — K)!. Doing the sum for all states (A, B), we get our answer. The complexity of this method is O(2 ^ (N / 2) * N).
Final Case: K = 2 The whole "meet in the middle" explanation worthed. We will do something very similar to solve this case. Suppose U1 and U2 are the unlucky numbers. Without loosing the generality, let's assume U1 <= U2.
Following "Principle of inclusion and exclusion" paradigm (google about it if you never heard before) we can write our solution as N! — |L1| — |L2| + |intersection between L1 and L2|. Again, by L1,2 I denote the number of routes which have a prefix sum equal to number U1,2. The |X| is again the cardinal of this set. Basically we can calculate |X| as for K = 1. The only problem remained is calculating |intersection between L1 and L2|.
The |intersection between L1 and L2| is the number of permutations which have a prefix sum equal to U1 and a prefix sum equal to U2. Since U1 <= U2, we can split a permutation from this set in 3 parts:
1/ p1, p2, ...pk such as a[p1] + a[p2] + ... + a[pk] = U1.
2/ pk+1, pk+2, ..., pm such as a[pk+1], a[pk+2], ..., a[pm] = U2 — U1. Note that a[p1] + a[p2] + ... + a[pm] = U2.
3/ The rest of elements until position n.
By a perfectly identical logic from K = 1 case, the number of permutations given those p[] would be k! * (m — k)! * (n — m)!.
So the problem reduces to: find all indices set p1, p2, ... and q1, q2, .. such as a[p1] + a[p2] + ... + a[pn1] = U1 and a[q1] + a[q2] + ... + a[qn2] = U2 — U1. Then, we can apply formula using n1 and n2 described above.
The first idea would be O(3 ^ N) — for each position from {1, 2, .., n} atribute all combinations of {0, 1, 2}. 0 means that position i is 1/, 1 means that position i is in 2/ and 2 means that position i is in 3/ . This would time out.
Happily, we can improve it with meet in the middle principle. The solution is very similar with K = 1 case. I won't fully explain it here, if you understood principle from K = 1 this shouldn't be a problem. The base idea is to keep (S1, S2, cnt1, cnt2) for both "left" and "right". (S1, S2, cnt1, cnt2) represents a subset which has sum of elements from 1/ equal to S1, sum of elements from 2/ equal to S2, in 1/ we have cnt1 element and in 2/ we get cnt2 elements. For a (S1, S2, cnt1, cnt2) state from "left" we are looking in the right for something like (U1 — S1, U2 — U1 — S2, i, j). We get O(3 ^ (N / 2) * N ^ 2) complexity.
Unexpected solution During the round, we saw a lot of O(2 ^ N * N) solutions passing. This was totally out of expectations. I believe if would make tests stronger, this solution won't pass and round would be more challenging. That's it, nothing is perfect. As requested, I'll explain that solution here.
Before explaining the solution, I assume you have some experience with "bitmask dp" technique. If you don't, please read before:
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=bitManipulation
http://codeforces.me/blog/entry/337
In this problem we'll assume that a is 0-based. For a mask, consider bits from right to left, noting them bit 0, bit 1 and so on. Bit i is 1 if and only if a[i] is in the subset which is in a bijective replation with the mask. For example, for mask 100011101 the subset is {a0, a2, a3, a4, a8}. I'll call from now on the subset "subset of mask". Also, the sum of all elements in a subset will be called "sum of mask" (i.e. a0 + a2 + a3 + a4 + a8). We'll explain the solution based by watashi's submission. 4017915
First step of the algorithm is to calculate sum of each mask. Let dp[i] the sum of mask i. Remove exactly one element from the subset of mask. Suppose the new mask obtained is k and removed element is j. Then, dp[i] = dp[k] + a[j]. dp[k] is always calculated before dp[i] (to proof, write both k and i in base 10. k is always smaller than i). Having j an element from subset of mask i, we can compute mask k by doing i ^ (1 << j). Bit j is 1, and by xor-ing it with another 1 bit, it becomes 0. Other bits are unchanged by being xor-ed by 0. This method works very fast to compute sum of each mask.
From now on, let's denote a new array dp2[i] = how many good routes can I obtain with elements from subset of mask i. Watashi uses same dp[] array, but for making it clear, in editorial I'll use 2 separate arrays. Suppose that CNT(i) is number of elements from subset of mask i. We are interested in how many ways we can fill positions {1, 2, ..., CNT(i)} with elements from subset of mask i such as each prefix sum is different by each unlucky number.
Next step of the algorithm is to see which sum of masks are equal to one of unlucky numbers. We mark them as "-1" in dp2[]. Suppose we founded a subset {a1, a2, ..., ax} for which a1 + a2 + ... + ax = one of unlucky numbers. Then, none permutation of {a1, a2, ..., ax} is allowed to appear on first x positions. When we arrive to a "-1" state, we know that the number of good routes for its subset of mask is 0.
Now, finally the main dp recurrence. If for the current mask i, dp2[i] = -1, then dp2[i] = 0 and continue (we discard the state as explained above). Otherwise, we know that there could exist at least one way to complete positions {1, 2, ... CNT(i)} with elements of subset of mask i. But how to calculate it? We fix the last element (the element from the position CNT(I)) with some j from subset of mask i. The problem reduces now with how many good routes can I fill in positions {1, 2, ..., CNT(i) — 1} with elements from subset of mask i, from which we erased element j. With same explanation of sum of mask calculations, this is already calculated in dp2[i ^ (1 << j)].
The result is dp2[(1 << N) — 1] (number of good routes containing all positions).
Editorial has been made by me and ll931110.
The authors of the problems:
Div.2 A & Div.2 B — me
Div.2 C & Div.2 D & Div.2 E — ll931110











About problem C. In the text of this problem I saw k<=10 and |a|<=10^5; But in tests I saw k>10. So I have a question. What is real size of k?
Upd: thanks ll931110 for his task C. It turned out that my browser Opera works incorrectly.
k<=10^9 (it's in the text)
Oh, no. My browser show me now that k<=10. Upd: I have made copy-past of k (1 ≤ k ≤ 109) Only in my comment I see limit of k correctly.
what is such stupid browser? :D
It's Opera Internet Browser. I will never us it in future. I installed Google Chrome 25 minutes ago. It works good.
I made a funny experiment with Opera. I opened problem C on full screen and it shows k<=10; I opened problem C in a small window it shows k<=10^9; I was surprised a lot. I opened E and also was shocked. It shows b+b+b+...+b Google Chrome shows b1+b2+b3+...+bj.
Now I regred that I used Opera. I spent one with a half of an hour to solve C with k<=10. I couldn't understand why I have Runtime error on pretest 9. I used O(n*k) memory and O(n*k) time.
Upd: It's 10.50.3296.0 version of Opera
is it new opera 15 or old 12?
On the text of this problem 1<=k<=10^9.
Can somebody see my solution to problem C, i use a little different approach however i'm getting WA and I think its because the mod. My solution: http://ideone.com/i2nxmK
it's wrong. there's only (a+b) % m = (a % m + b % m) % m and (a*b) % m = (a % m * b % m) % m.
To calculate a/b % m we have to find b^(-1), such elements as b^-1 * b = 1(mod m), and calculate a*b^-1 % m. For this way you can use Euler's Theorem.
Also your mistake is (a — 1) % m. We have to find a non-negative remainder, but (a -1) % m can be negative. For this way you should calculate a + m-1 instead of a-1.
My idea for problem E when K=2 please correct me if I'm wrong
when k=2 the answer is:
answer = n! — (the number of permutations that passes k[0] + the number of permutations that passes k[1] — the number of permutations that passes both k[0] and k[1])
to calculate the number of permutations that passes both k[0] and k[1]:
find the number of ways to choose two Non-intersecting sets from the the input integers so that the sum of elements in first set is K[0] and the sum of elements in the second set is k[1]-k[0] (assuming k[1]>k[0] if not swap them) then for each way we have (u! * v! * (n-v-u)!) permutation satisfy condition above where u is the number of elements in first set and v is the number of elements in second set
to calculate the number of ways to choose two Non-intersecting sets from the the input integers one can use meet in the middle attack but the number of permutations depends on the size of two sets so:
for i=1 to N do
for j=1 to N do
let P = the number of ways to choose two non-intersecting sets from the the input integers so that the sum of elements in first set is K[0] and the sum of elements in the second set is k[1]-k[0] and the first set contain i integers and the second set contains j integers
add to answer i! * j! * (n-i-j)! * P
end for
end for
this is my guess to problem E , I didn't code it so I'm not quite sure that my idea is ok
Yes, that's generally what we intended. Unfortunately, we overlooked the bitmask solution, which is a good (bad) thing for someone..
Good Contest and awesome editorial(Nice work for your 1st contest :-) )...Hungry's Second sol.n Good One!! only 4-5 lines of code...I coded for sieve for abt 45 mins for getting it right :-(...I have done it before but I still took large time to code ...how can I reduce it...Btw there's a typo in editorial Stieve--->Sieve.
Thank you for the feedback! I corrected the typo now.
Can anyone provide a link of solution for problem E, that uses the meet-in-the-middle technique explined in the tutorial. As far as I saw most used all subsets.
http://pastebin.com/VgccEqJi
Here is our official solution. I hope that helps you.
Chinses user can't load that page(I scale the wall).But gists we can load.May you put another one in gists to ease other chinese people?
Sure.
https://gist.github.com/anonymous/5943298
Thanks.
I came up with a different solution for C that runs in O(N+logK^2) — http://codeforces.me/contest/327/submission/4018240 . It can be easily optimized to O(N+logK).
Can anyone give hints for dp solution of problem E?
very very good editorial... one of the best i have read in cf...really...and the problem set was excellent.\m/
For C, we have to calculate modular inverse. Since the denominator is very large, we are using (1/(a%m))%m == (1/a)%m. I can verify this using Fermat's Little Theorem. But I want to ask whether its always true(even when m is not prime). Also how to prove it?
it's true if : gcd( a , MOD ) == 1 then a ^ (MOD-2 ) % MOD == ( 1 / a )
obviously gcd(a,m)==1 for the inverse to exist. I want to ask whether (1/a)%m == (1/(a%m))%m, is always true, given the inverse exists.
It is. When adding/subtracting/multiplying/dividing one can take both numbers modulo mod.
But it is important to mention that euler's function isn't equal to mod - 2, and amod - 2 is correct only for prime mod
Thanks!
a and m should be coprimes
C is cool, but really hard. I got to the sum of geometric progression, but didn't know how to perform the division with mod :( Have to learn about modular inverse... Anyway, thanks for the contest!
Do you intend on giving the complicated solution for C, because I am really interested how does this matrix multiplication solution looks like.
I believe we'll update the editorial tomorrow with matrix multiplication for C and dp bitmasks for E (as requested). Stay turned! :)
L.E. As promised, both solutions are added. If you have anything else which you'd like to see in the editorial, please write a comment.
About problem B.
We can write sequence {10^7-N,10^7-N+1,...,10^7-N+(N-1),10^7-N+(N)}.
simple, print(n,2n-1)
Problem C: Why do you say complexity is O(N*logK) when you have S which is calculated only once and after that you have at most N 2^i calculations, which means the complexity is O(NlogN+logK) which is almost the same as the matrix multiplication solution. However, I am still curious to see it :)
Actually, you can calculate 2i for i from 0 to n - 1 in O(n) time, so the complexity is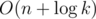 .
.
Yes, you are right! Using a little more memory of course. Anyways, this means it's better than the matrix solution, but its always good to know various algorithms doing the same thing isn't it? This a truly excellent editorial!
Hi, I know this is not the best place to put this but please see the people in cf-191 standings at position 82.84,85,86 highly suspicious names and solution timings
Well, I didn't konw there're these tutorial blogs here before! What a pity! That's really good for writors to write these blogs. I benefited a lot from it. And thanks! ^_^
Problem B:
I write 5000001 5000002 5000003 ... my code 4024979
I got TLE for problem D, just because of slow output :(
i was getting TL on C# too. When i changed enqueueing strings while DFS
and output like this
to
and output
It passed with 1.5 seconds.
I'm curious about the testing. In Problem B(Hungry Sequence) how do you check if a solution is correct? I can only think of an O(n*n) brute force to check if the condition "For any two indices i and j (i < j), aj must not be divisible by ai" holds
We check if solution is in increasing order. Then, we take each number a[i]. We check if 2 * a[i], 3 * a[i], ..., k * a[i] exist in the sequence. If one of them exist, then the solution is wrong. We stop iterating k when k * a[i] > VMAX (here, VMAX is 10^7).
It may look slow, but it isn't. Worst case, we need to make O(VMAX / 2 + VMAX / 3 + ... VMAX / N) operations (assuming that {2, 3, ..., N} would be a good solution). But VMAX / 2 + VMAX / 3 + ... + VMAX / N works faster than VMAX / 2 + VMAX / 3 + ... + VMAX / VMAX. Also, we know from math that VMAX / 2 + VMAX / 3 + ... + VMAX / VMAX ~ O(VMAX * logVMAX). So our solution works faster than O(VMAX * logVMAX).
I hadn't realized that you can add a hash — or a simple array — to make the sieve work. Thanks :)
If in the first copy, at the position i is either 0 or 5, we have to calculate the sum 2 ^ i + 2 ^ (i + n) + 2 ^ (i + 2 * n) + … + 2 ^ (i + (k – 1) * n).
should't it be (i-1) instead of i everywhere because we just fount out "To sum it up: If S[i] is 0 or 5 we add to the answer 2 ^ (i – 1). "
Thank you! I'm sorry for the mistake. I added a phrase saying that by using a substitution, i refers to i — 1 from that point.
actually i stopped practicing on codeforces because of bad editorials(though i have participated in 2-3 contests only)...i came back after long time and found this editorial very useful which taught me very much..it shows how seriously you took it .hope to see more like these and yes now i will be regular at codefirces :)
Excellent Tutorial..............
yeah,the tutorial explained everything in great detail. Very excellent.
It was a great round and thanks for this excelent tutorial!
Could someone please help me to figure out what's wrong with my solution of C. Code. I try to use the same way as “Exponentiation by squaring”. If k is even I calculate number of variants for k / 2 recursively and then sum this value and this value multiplied by appropriate power of 2. Respectively, for odd k I calculate sum for single string and shifted (k — 1). This solution even passes several first tests but then fails with a wrong answer on a big test which isn't shown entirely. The question is if I have conceptual error in my solution and this idea doesn't work at all (why?) or I have bug in my implemetation
Really best tutorial ever in codeforces. thanks sir for great tutorial!!!
Вроде есть квадратное решение задачи Игра с переворачиванием.
in A is the author talking about Kadane's Algo for O(N) approach??
Yes indeed
can someone check my solution for problem D: It's getting TLE at testcase 36
my solution link
Hungry solution trick, start from last and decrement till n the contraints will help to make sure it is even starting elelment can not divide any element
can anyone share o(n) solution using dp for flipgame?
Notations:
$$$a\left[l,r\right]=\left[{a}_{l},{a}_{l+1},...,{a}_{r}\right]$$$
$$$pre\left[i\right]=$$$ Number of 1s in $$$a\left[1,i\right]$$$ (Assuming 1-based indexing)
Explanation:
After applying the operation on the indices $$$i,j \left(1\le i\le j\le n\right)$$$, Number of 1s in the array
$$$=$$$ (Number of 1s in $$$a\left[1,i-1\right]$$$) + (Number of 0s in $$$a\left[i,j\right]$$$) + (Number of 1s in $$$a\left[j+1,n\right]$$$)
$$$=\left(pre\left[i-1\right]\right)+\left(j-i+1-\left(pre\left[j\right]-pre\left[i-1\right]\right)\right)+\left(pre\left[n\right]-pre\left[j\right]\right)$$$
$$$=\left(j-2\times pre\left[j\right]\right)-\left(i-1-2\times pre\left[i-1\right]\right)+pre\left[n\right]$$$
Let $$$f\left[k\right]=k-2\times pre\left[k\right]$$$
$$$\Rightarrow $$$ Number of 1s in the array $$$=f\left[j\right]-f\left[i-1\right]+pre\left[n\right]$$$
$$$\therefore $$$ Maximum Number of 1s in the array $$$=f\left[j\right]-min_{1\le i\le j}f\left[i-1\right]+pre\left[n\right]$$$
$$$\Rightarrow $$$ Maximum Number of 1s in the array $$$=f\left[j\right]-min_{0\le i\le j-1}f\left[i\right]+pre\left[n\right]$$$
Let $$$g\left[k\right]=min_{0\le i\le k}f\left[i\right]$$$
$$$\Rightarrow $$$ Maximum Number of 1s in the array $$$=f\left[j\right]-g\left[j-1\right]+pre\left[n\right]$$$
We can compute $$$pre\left[k\right]$$$, $$$f\left[k\right]$$$ and $$$g\left[k\right]$$$ in $$$O\left(n\right)$$$.
After that, we can get our final answer using $$$max_{1\le j\le n} (f\left[j\right]-g\left[j-1\right]+pre\left[n\right])$$$, which can also be computed in $$$O\left(n\right).$$$
In problem C , we can compare with geometrical series directly for , (2 ^ 0 + 2 ^ n + 2 ^ (2 * n) + … + 2 ^ ((k – 1) * n) this series, So , we can write S = ((2^n)^x — 1) / (2^n-1)
another solution for B...
suppose we have number x the next devisor of x is 2*x so.... the max n is 10^5 we can just loop from 1 to n and print (n-1+i) so that in the worst case where n=10^5 you can check that in this loop the first number will be printed is 9999 but we will not reach 2*9999 in this loop
you can see my submission for better understanding my approach 238886889