Imagine that we have successfully processed first i - 1 bowls, i.e. we know height of the bottom yj for every bowl j (1 ≤ j < i). Now we are going to place i-th bowl. For each j-th already placed bowl, we will calculate the relative height of the bottom of i-th bowl above the bottom of j-th bowl, assuming that there are no other bowls. Lets denote this value by Δi, j. It is obvious that height of the new bowl is equal to the maximal of the following values: yi = max(yj + Δi, j).
Now I will describe how to calculate Δi, j. Firstly, consider two trivial cases:
I. ri ≥ Rj: bottom of i-th bowl rests on the top of j-th. Then Δi, j = hj.
II. Ri ≤ rj: bottom of i-th bowl reaches the bottom of j-th. Then Δi, j = 0.
Then there are three slightly more complicated cases.
1. ri > rj: bottom of i-th bowl gets stuck somewhere between the top and the bottom of j-th,
touching it's sides. From the similarity of some triangles we get that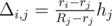 .
.
2. Ri ≤ Rj: top of i-th bowl gets stuck somewhere between the top and the bottom of j-th,
touching it's sides. From the similarity of some triangles we get that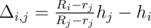 .
.
3. Ri > Rj: sides of i-th bowl touch the top of j-th in it's upper points. Then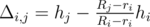 .
.
Note that, for example, cases 1 and 2 do not exclude each other, so the final value of Δi, j is equal to the maximum of the values, computed in all three cases.
Note that if the calculated value of Δi, j is negative, the result should be 0. Thanks to adamax for pointing it.
Now I will describe how to calculate Δi, j. Firstly, consider two trivial cases:
I. ri ≥ Rj: bottom of i-th bowl rests on the top of j-th. Then Δi, j = hj.
II. Ri ≤ rj: bottom of i-th bowl reaches the bottom of j-th. Then Δi, j = 0.
Then there are three slightly more complicated cases.
1. ri > rj: bottom of i-th bowl gets stuck somewhere between the top and the bottom of j-th,
touching it's sides. From the similarity of some triangles we get that
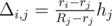 .
.2. Ri ≤ Rj: top of i-th bowl gets stuck somewhere between the top and the bottom of j-th,
touching it's sides. From the similarity of some triangles we get that
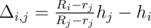 .
.3. Ri > Rj: sides of i-th bowl touch the top of j-th in it's upper points. Then
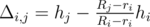 .
.Note that, for example, cases 1 and 2 do not exclude each other, so the final value of Δi, j is equal to the maximum of the values, computed in all three cases.
Note that if the calculated value of Δi, j is negative, the result should be 0. Thanks to adamax for pointing it.











It seems that it's case 2, but the formula will give a wrong answer.