Если aj делится на ai, то тогда ai ≤ aj. Тогда число, на которое будут делиться все остальные числа будет не более чем любое выбранное число. То есть единственный возможный кандидат — это минимум в массиве. Поэтому просто проверим, что все элементы массива делятся на минимальный элемент.
Легко видеть, что Ксюша не сможет закончить ее путешествие, если существует последовательность подряд идущих # длиное более чем k.
Первое наблюдение: мы не будем волноваться о том, как выглядят строки на самом деле, вся информация, которая нам нужна — это количество пар-символов вида: {0, 0}, {0, 1}, {1, 0}, {1, 1}. Посчитаем эти количества и будем следовать следующему жадному алгоритму:
Для первого игрока: будем брать сначала {1, 1}, если их нет, то {1,0}. Если их нет, то {0, 1} и, в последнюю очередь, будем брать {0, 0}.
Для второго игрока похожая стратегия: сначала {1, 1}, потом {0, 1}, потом {1, 0} и, в последнюю очередь, {0, 0}.
После этого сравним у кого получилось больше единичек.
Любой путь из верхней левой клетки в правую нижнюю состоит ровно из n + m - 1 клеток. И все они должны быть покрашены в разные цвета. Значит n + m - 1 ≤ k. Исходя из маленьких ограничений на k можно предположить, что брут-форс будет работать. Единственная оптимизация для получения действительно правильного решения — это некоторая канонизация раскрасок. Будем идти по всем клеткам в некотором порядке и красить их согласно следующим условиям. Если i > j, тогда цвет i встречается позже цвета j. После такого перебора мы получим примерно миллион различных шаблонов для максимального теста.
Далее, просто будем сопоставлять уже покрашенные клетки с каждым шаблоном и считать, сколько различных перестановок цветов подходят к данному шаблону.
После прочтения условия, можно понять, что все, что нам нужно — это посчитать количество решений уравнения (a + b + c)3 - a3 - b3 - c3 = n в положительных целых числах.
Ключевое наблюдение это: 3(a + b)(a + c)(b + c) = (a + b + c)3 - a3 - b3 - c3, после чего мы можем просто вычислять все делители числа  и идти по всем делителям x = a + b, таким что
и идти по всем делителям x = a + b, таким что 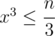 ? далее будем идти по делителям y = (a + c) ≥ x, где
? далее будем идти по делителям y = (a + c) ≥ x, где 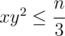 и в конце будем вычислять z = (b + c), такое что
и в конце будем вычислять z = (b + c), такое что 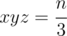 .
.
После этого, решим систему a + b = x, a + c = y, b + c = z и добавим количество подходящих решений к ответу.
Можно заметить, что в этой задаче просят посчитать 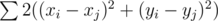 для всех целых точек внутри многоугольника (или на его границе). Можно заметить, что мы можем обрабатывать иксы и игреки независимо.
для всех целых точек внутри многоугольника (или на его границе). Можно заметить, что мы можем обрабатывать иксы и игреки независимо.
Для каждого x определим yleft, yright таким образом, что все точки (x, y), где yleft ≤ y ≤ yright лежат внутри многоугольника и отрезок [yleft, yright] максимально возможный.
Теперь будем считать, что мы имеем a1, a2, ..., ak различных точек для каждого фиксированного x (a1 соответствует x = - 106, a2 соответствует x = - 106 + 1 и так далее).
Теперь требуемый ответ это a2a1 + a3(a2 + 22a1) + a4(a3 + 22a2 + 32a1) + ...
Можно заметить, что
(a2 + 22a1) - a1 = a2 + 3a1,
(a3 + 22a2 + 32a1) - (a2 + 22a1) = a3 + 3a2 + 5a1,
и так далее.
Поэтому достаточно предпросчитать частичные суммы вида a2 + 3a1, a3 + 3a2 + 5a1, a4 + 3a3 + 5a2 + 7a1 (разность между двумя соседними суммами составляет 2(ai + ... + a1), поэтому мы можем делать это за O(k)).
После предпросчета достаточно сложить полученные результаты.
Будем считать что у нас есть структура данных, которая позволяет осуществлять следующие операции:
добавить точку (x, y) в структуру;
сдвинуть все точки структуры на вектор (dx, dy);
узнать как много точек (x,y), удовлетворяющих x ≤ xbound, y ≤ ybound;
получить все элементы, которые на данный момент находятся в структуре;
Для каждой вершины дерева мы будем хранить указатель на структуру такого вида.
ОБъясним, как нужно обновлять структуры. Мы будем обрабатывать все вершины в порядке обхода в глубине, и если мы находимся в листе, то мы будем создавать структуру с единственным элементом (0, 0).
В противном же случае, мы будем сортировать структуры сыновей по их размеру в убывающем порядке и будем присваивать указатель наибольшей структуры указателю на текущую вершину (здесь нужно не забыть сдвигать структуру на (1, вес ребра)).
После этого будем идти по всем сыновьям вершины и делать следующее:
Сдвинем структуру на (1, вес ребра);
Возьмем все элементы структуры;
Для каждого элемента (x, y) ответим на запрос xbound = L - x, ybound = W - y (используем родительскую структуру);
Добавим элементы по одному в структуру;
После этого ответим на запрос xbound = L, ybound = W и добавим элемент (0, 0).
Сумма полученных результатов по всем запросам и будет ответом. Легко видеть, что мы совершим не более чем 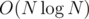 запросов и операций добавления.
запросов и операций добавления.
Осталось только объяснить, как создать нужную нам структуру данных.
Существует несколько способов сделать это, один из них:
Будем иметь маленькие подструктуры у которых размеры являются степенями двойки;
Каждая структура — это двумерное дерево отрезков;
Мы можем добавлять элемент следующим образом: если нет подструктуры размера 1, тогда создадим ее, иначе же возьмем все структуры размерами 1, 2, 4, ..., 2k и перестроим в структуру размера 2k + 1.
Сдвиг: достаточно помнить вектор сдвига для каждой подструктуры;
Ответ на запрос: идем по подструктурам и суммируем результаты.











anyone know how to solve Problem D,please help me , I've read the edutial again and again , but still can't understand
how to determine yleft and yright
Okay, I assume there are several approaches to do that. One of them — just go over every side of polygon and update y_left and y_right for every x it covers. For example, if we have side with vertices (x1, y1) — (x2, y2) than it covers range [x1,x2] and for every x you can determine corresponding y and two integer values which are the closest to it. But it requires careful implementation, because not both of those y are inside the polygon.
I mention E div 2. Can you explain how to get all these x,y,z quicker than look at all integer in the interval [1..n]?
Can you please fix the C problem since the god damn program asks for one thing, you guys in the tutorial show another thing and the people who have solved it used a whole different method. It's really frustrating to start a problem and then realise that the enunciation is not translated properly or does not properly tell you what you have to do. Thanks.
Does the solution for E have (nlogn)*(log2n) complexity? nlogn for the number of queries, and log2n for the complexity of each query. Or is there an easier way to solve it?
You can expend log(n) for each query if you use a persistent segment tree.
Cant the E problem be solved using centroid decomposition, I feel maintaining the data structures becomes easy, and we have the flexibility to calculate the number of good pairs passing through the centroid in $$$O(N)$$$ or even $$$O(NlogN)$$$ per centroid.
Here in this solution, it is not required to do shifting operations (as mentioned in the editorial) and the implementation would become relatively easier. It's just enough to count the number of pairs $$$(x,y)$$$ where $$$x <= x_i$$$ and $$$y <= y_i$$$, which can be solved by sorting + ordered_set. So it takes $$$O(NlogN)$$$ per centroid, and total complexity is $$$O(Nlog^2(N))$$$
Submission: 280804865
ASHWANTH_K I am using centroid decomposition to solve this problem. When make dfs(centroid), I store data in map<pair<int, int>, int> data; // data[{len, weight}] = cnt; But I do not know how to calculate the number of paths that satisfy len <= l and weight <= w efficiently. Could you explain more details about your implementation?
Here is my TLE submission