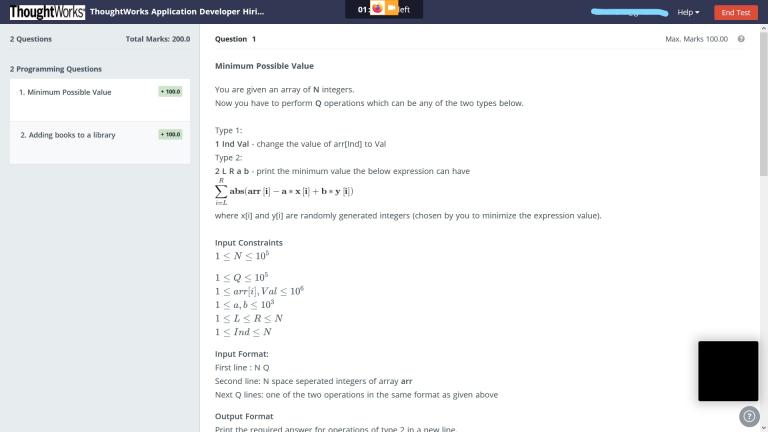
I was giving this hiring contest ( already over ). I am stuck at this question. Needed some help
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
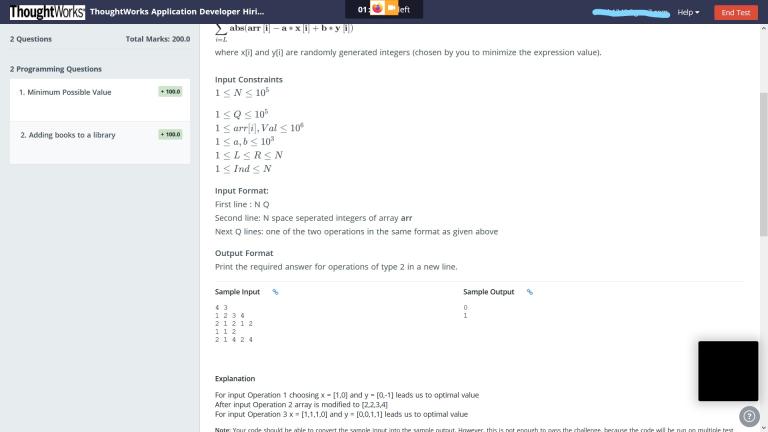
I was giving this hiring contest ( already over ). I am stuck at this question. Needed some help


| Name |
|---|



The only conclusion I was able to reach is that for any query L, R, a and b, let g be the gcd of a, b. Then
But it is just an optimization of bruteforce.
Since $$$max(a, b) \le 10^3$$$, an optimization can be to build segment tree over the array, the nodes of which, will contain $$$10^3$$$ values, each corresponding to the required range sum as the gcd varies from $$$1$$$ to $$$1000$$$.
Update is $$$O(M \cdot \log N)$$$ and query is $$$O(\log N)$$$ with $$$O(N \cdot M)$$$ memory, where $$$M = max(a, b)$$$.
Since $$$M \le 10^3$$$, this could probably be fit into TL depending on how much it is.