I was giving this hiring contest ( already over ). I am stuck at this question. Needed some help
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
I was giving this hiring contest ( already over ). I am stuck at this question. Needed some help


| Название |
|---|



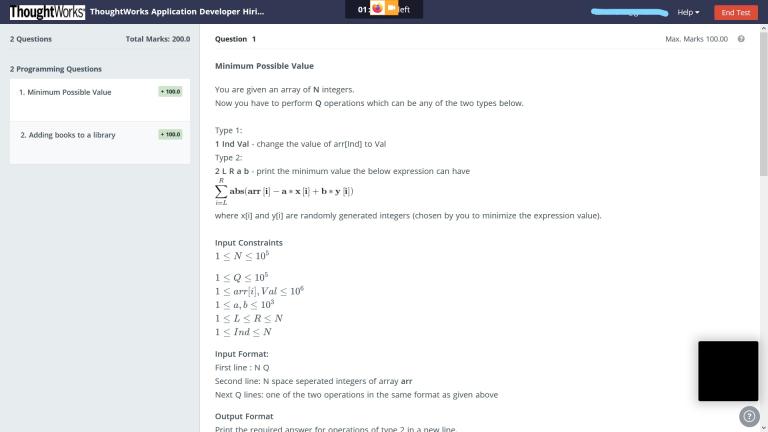
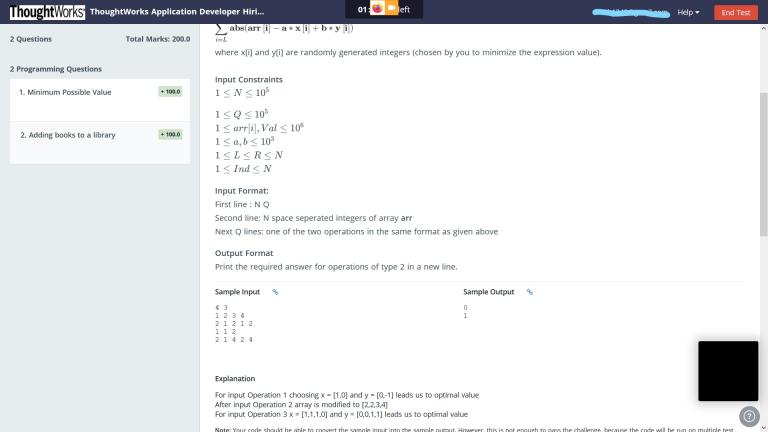
The only conclusion I was able to reach is that for any query L, R, a and b, let g be the gcd of a, b. Then
But it is just an optimization of bruteforce.
Since $$$max(a, b) \le 10^3$$$, an optimization can be to build segment tree over the array, the nodes of which, will contain $$$10^3$$$ values, each corresponding to the required range sum as the gcd varies from $$$1$$$ to $$$1000$$$.
Update is $$$O(M \cdot \log N)$$$ and query is $$$O(\log N)$$$ with $$$O(N \cdot M)$$$ memory, where $$$M = max(a, b)$$$.
Since $$$M \le 10^3$$$, this could probably be fit into TL depending on how much it is.