Количество различных строк длины 2: 262 = 676, а суммарная длина всех строк не превосходит 600. Это значит, что длина ответа не превосходит 2. Поэтому можно просто проверить все строки длины 1 и 2.
Построим двудольный граф с n вершинами (для сотрудников) в одной доле, и m вершинами (для языков) в другой. Если сотрудник знает язык, значит должно быть ребро между соответствующими вершинами. Теперь задача выглядит понятнее: нужно добавить в граф минимальное количество ребер, чтобы появилась компонента связности, содержащая всех n сотрудников. Очевидно, что это число равно количеству компонент связности, включающих хотя бы одного сотрудника, минус 1. Но есть одно исключение (претест #4): если изначально вообще никто не знает ни один язык, то ответ равен n, так как мы не можем добавлять ребра напрямую между людьми.
Для m = 3, n = 5 и m = 3, n = 6 решения не существует.
Научимся строить ответ для n = 2m, где m ≥ 5 и нечетное. Расставим m точек на окружности достаточно большого радиуса — это будет внутренний многоугольник. Чтобы получить внешний многоугольник, умножим все координаты внутреннего на 2. Более точно (1 ≤ i ≤ m):
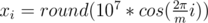
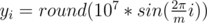
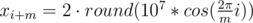
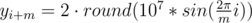
Если m четное, построим решение для m + 1 и удалим по одной точке из каждого многоугольника. Если n < 2m, удалим 2m - n точек из внутреннего многоугольника.
К сожалению, такое решение не работает для m = 4, n = 7 и m = 4, n = 8.
Альтернативное решение — поставить m точек на выпуклой функции (например, y = x2 + 107), и n - m точек на вогнутой функции (например, y = - x2 - 107). Так решал rng_58 — 3210150.
Заметим, что горизонтальные и вертикальные разрезы независимы. Рассмотрим любую горизонтальную линию: она содержит m единичных отрезков, и в любой ситуации всегда возможно уменьшить длину неразрезанной части так, как этого хочет игрок. Представим, что игрок наращивает отрезок от края поля, увеличивая его длину на 1 за раз. Каждый раз суммарная длина неразрезанной части уменьшается либо на 0, либо на 1. В конце, понятно, достигает 0.
То же самое верно и для вертикальных линий. Значит, если бы не было начальных разрезов, игра превратилась бы в ним с n - 1 кучками по m камней и m - 1 кучками по n камней. Решается простой формулой.
Начальные k разрезов добавляют только техническую сложность. Для каждой вертикальной/горизонтальной линии, содержащей хотя бы один разрез, размер соответствующей кучки нужно уменьшить на суммарную длину всех разрезов на этой линии.
Как делать первый ход в ниме: пусть res — результат игры, а ai — размер i-ой кучки. Тогда результат игры без i-ой кучки — 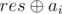 . Мы хотим заменить ai на какое-то x, чтобы
. Мы хотим заменить ai на какое-то x, чтобы 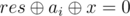 . Понятно, что единственное подходящее значение
. Понятно, что единственное подходящее значение 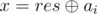 . Итоговое решение: находим такую кучку, что
. Итоговое решение: находим такую кучку, что 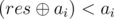 , и уменьшаем ai до
, и уменьшаем ai до 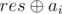 .
.
Пусть зафиксирован набор подзадач, которые мы будем решать. Давайте определим, в каком порядке их нужно решать. Понятно, что легкие подзадачи (и сложные подзадачи с probFail = 0) в любом случае не упадут. То есть наше штрафное время не меньше времени отправки последней такой <<надежной>> подзадачи. Значит, в первую очередь нужно решить все такие подзадачи. Подзадачи с probFail = 1 вообще не имеет смысла решать. Рассмотрим подзадачи с 0 < probFail < 1. Пусть есть две подзадачи i и j, которые мы решаем подряд. Посмотрим, в каком случае выгодно их решать в порядке i, j, а не наоборот. Мы не учитываем остальные задачи, так как они ни на что не влияют.
(timeLargei + timeLargej)(1 - probFailj) + timeLargei(1 - probFaili)probFailj < (timeLargei + timeLargej)(1 - probFaili) + timeLargej(1 - probFailj)probFaili
- probFailj·timeLargej - timeLargei·probFailj·probFaili < - probFaili·timeLargei - timeLargej·probFaili·probFailj
timeLargei·probFaili(1 - probFailj) < timeLargej·probFailj(1 - probFaili)
timeLargei·probFaili / (1 - probFaili) < timeLargej·probFailj / (1 - probFailj)
Получается, что если отсортировать подзадачи по данному компаратору, будет оптимальный порядок решения. Заметим, что подзадачи probFail = 0, 1 тоже отсортируются правильно, то есть не являются частными случаями.
Вернемся к исходной задаче. Первым делом отсортируем все задачи полученным компаратором — ясно, что в другом порядке решать никогда не выгодно по времени, а количество очков от порядка не зависит. Посчитаем такую динамику: z[i][j] = пара из максимального матожидания суммы очков и минимального штрафного времени при данной сумме очков, если мы рассмотрели первые i задач, и прошло j реальных минут контеста. Возможно 3 перехода:
либо мы не трогаем i-ую задачу: переходим в z[i + 1][j] с такими же матожиданиями
либо мы решаем только легкую подзадачу: переходим в z[i + 1][j + timeSmalli], при этом очки увеличиваются на scoreSmalli, и штрафное время — на timeSmalli (мы как бы считаем, что будем решать i-ую задачу в самом начале контеста)
либо мы решаем обе подзадачи: переходим в z[i + 1][j + timeSmalli + timeLargei], при этом очки увеличиваются на scoreSmalli + (1 - probFaili)scoreLargei, и штрафное время становится равным timeSmalli + (1 - probFaili)(j + timeLargei) + probFaili·penaltyTime(z[i][j]), где penaltyTime(z[i][j]) — значение матожидания штрафного времени из динамики
Итоговый ответ — наилучшее из значений z[n][i], (0 ≤ i ≤ t).
Матожидание очков может быть числом порядка 1012 с 6 знаками после точки, то есть его нельзя хранить в типе double абсолютно точно, а любая погрешность в вычислении матожидания очков может привести к ошибке в матожидании времени (претест #7). Чтобы этого избежать, можно, например, домножить все вероятности на 106, и считать первое матожидание в целых числах.
277E - Бинарное дерево на плоскости
Если бы не было ограничения на "бинарность", задача бы решалась простой жадностью. Каждая вершина дерева (за исключением корня) должна иметь ровно одного предка. При этом каждая вершина может быть родителем для любого количества вершин.
Назначим каждой вершине i (исключая корень) в качестве предка такую вершину pi, что ypi > yi и при этом pi — ближайшая к i. Перенумеруем все вершина в порядке невозрастания y. Очевидно, что pi < i (2 ≤ i ≤ n). То есть мы таким образом задали корневое дерево, в котором все дуги идут вниз, и оно минимально по длине.
Теперь вспомним про "бинарность". Но она на самом деле мало чего меняет: жадность превращается в min-cost-max-flow на той же матрице расстояний, но только теперь в каждую вершину должно приходить не более 2 единиц потока.











There should be said a word about overlapping in the editorial on 278B. it s not obvious that it doesnt matter
although there could be several different solutions for a particular problem, I guess using disjoint set data structure(including some modifications) would be an easier solution for 277A, isn't it?
The tutorial only talks about the idea, involving connected component, and of course you can use disjoint set to deal with it, while bfs,Floyd-Warshall,etc. also works.
Please explain me, why in 277B there is no solution for n=6, m=3?
{(0,0), (10,0), (0,10),(1,1),(3,2),(6,3)}
(0,0),(1,1),(3,2),(6,3),(10,0) makes a convex polygon of 5 vertices, which is more than m=3
Thank you! :) I read it wrong...:(
Could someone explain 227E — Binary Tree: how will the flow graph look like? Solution codes don't give me a hint :(
For each vertex of the tree you need to create two vertices, the first one having an incoming edge of capacity equal to 2 and cost equal to zero from the source, the second one must have an outcoming edge to the sink with unit capacity and, again, zero cost. Also, you should add edges from all vertices of the first cathegory to all vertices of the second cathegory (unit capacity and cost equal to the distance). If your maxflow equals to n — 1, then your answer is correct, else there is no suitable binary tree.
В 277B можно повернуть один из многоугольников на небольшой угол, тогда никаких особых случаев не возникает=)
Зато может случайно получиться, что 3 точки лежат на одной прямой.
Если крутить на 'малый' угол, например 2 * PI / (N ^ 2), то такого не должно возникнуть, если я не ошибаюсь.
Например, решение 3216899 поворачивает на угол 10 - 6. Если поменять угол на 2π / n2, то не работает при n = 100, m = 72. Хотя конечно можно так подобрать радиусы и угол, чтобы работало на всех возможных тестах.
Ну я имел ввиду конечно же 2 * PI / (M ^ 2), по крайней мере такое у меня получает АС...
В моем решении второй многоугольник имеет радиус 2*R + 100 (где R = 10^6) и повернут на угол Pi/(10*N). Если сделать точный чертеж и нарисовать продолжения всех диагоналей, то становится понятно, что как ни группируй, получается максимум половина точек в выпуклой оболочке. Трех точек на одной прямой тоже не должно встретиться в таком случае.
in 278-B if the range in bigger like n<=10^6 and length of each string be atmost 1000 or 2000 then what will be the approach?
i think may be the use of hashing can be good.
There exists a very easy solution using suffix structures such as suffix tree, suffix automaton and suffix array. In the first two cases you need just to find a shortest and lexicografically smallest path, which is impossible to follow, in the last case you can build an LCP (largest common prefix) array and binsearch for the length of the answer (you can check whether the answer exists just by counting the number of different substrings of some length in linear time).
UPD. I'd advise you to read yourself about these structures (you should start with suffix array).
A solution involving a suffix structure is by definition not "very easy" ;)
But consider all strings of length <= 5. There are over 11 million of them, and only around under 5 million of these can be substrings of any string from a collection with total size under 1000000. So just mark off the used substrings, and then pick the smallest unused one.
By the phrase "very easy" I meant: you don't need to think a lot to guess such a solution.
But your solution is great and "very easy" in all means:).
Как доказать в 277В что розставляя по методу rng_58, не появится трех точек лежащих на одной прямой? Я так понял что это гарантируется сдвигом параболы, но подставляя крайние точки в уравнение прямой я так и не смог получить(на данный момент) строго доказательства.
Судя по тому что у Zlobober что-то очень похожее упало непонятно как это доказать. Возможно просто совпало, что при таких константах не получается. У меня чуть-чуть другие формулы 3211051 и вроде с такими все доказывается просто, т.к прямые проходящие через две точки одно параболы не заходят в четверть, где лежит другая.
А когда будет разбор 277D?
Hi,i'm solved Div 1. B too. But i cant understand how this problem check program work?..i'm very intrested of this..can sb tell me ?
can anyone give me some proof according to problem 277B — Set of Points about rng_58's solution ?
ah, maybe it is a little silly...
I have a little problem to compute the expected with penalty. Denote the corresponding var with ti, pi, then we have 4 situations:
then sum it up, it is ti(1-pi)+(ti+tj)(1-pj), not ti(1-pi)pj+(ti+tj)(1-pi). where am I wrong?
Read the problem statement: "By the Google Code Jam rules the time penalty is the time when the last correct solution was submitted."
Read problem statement more carefully:
By the Google Code Jam rules the time penalty is the time when the last correct solution was submitted.so, the last line
i AC, j AC (1-pi)(1-pj) ti+tj
ahhh, I thought it would be for each problem solved.
many thx to all.
Why in 277D GOOGLE CODE JAM, we are not doing time penalty calculation in an integer as doing the calculation in double may lead to precision error. Is it because the time is only 1560?