Автокомментарий: текст был обновлен пользователем aleex (предыдущая версия, новая версия, сравнить).

Auto comment: topic has been updated by aleex (previous revision, new revision, compare).

thanks for fast editorial!

Very interesting to know how many people got AC on Div.1 D without using google :)

Instant editorial

Это адекватно, что 1) С сдало гораздо меньше человек, чем D 2) D очень тупая задача на гугление формулы (Я на контестах никогда ничего не гуглю, т.к. на любом нормальном соревновании гуглить нельзя) мне очень не понравилось, что задача на комбинаторику (одна из моих любимых тем) решается через никому не известную теорему

Here is the proof of the generalized Cayley's formula (link from Wikipedia sources).

I failed to work this out myself and lost an hour :(. Next time I'll try Google first.

Great contest, but It would have been better if the setter had allowed only O(n) to get accepted in DIV 2D.

In A Div2 If v=n-1 Isn't the answer equal to n-1?

For E, I think the maximum number of primes is 9 instead of 8 since 3 is also a prime

Can anyone explain what "So to count the answer just have two arrays cnt[0][x] to store elements from even positions and cnt[1][x] for odd positions. Then iterate i from 1 to n and add to the answer cnt[imod2][prefi]. After you processed i, increase cnt[imod2][prefi] by 1" mean in Editorial of Problem 1109A

Author's solution should be included too.

I solved 1109D - Sasha and Interesting Fact from Graph Theory without using the generalization of Cayley's formula — because I didn't know that generalization.

I tried to get O(n²) solution first. I iterated over the distance between a and b (just like the editorial describes) and then over the degree of the fake vertex (i.e. total degree of the path between a and b). Prufer codes give us a way to compute the number of trees where one vertex has some given degree: it means that this number must occur exactly deg - 1 times in the sequence of size n - 2, so the formula is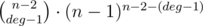 for a tree with n vertices. We multiply that by some other stuff like (edges - 1)! for rearranging vertices on the path etc. This way we get O(n²) solution and to make it faster we need to compute the following sum fast for two constants C and D (I got something similar after simplifying formulas):

It's easy to make a story for that to get a formula: we want to choose i of C soldiers, and then choose one of D colors for every chosen soldier. Instead, we can say that every soldier gets one of D + 1 types and the last type D + 1 means that this soldier is not chosen at all. So the sum is equal to:

For div.2 problem B please anyone explain following test case n=8 1 1 1 1 1 1 100 100

In Div1D, when we fix edges, why are we taking combinations of edges-1 vertices and not permuations ?

I have TL with this code!

https://pastebin.com/ds9FkhiC

Do you know why?

Auto comment: topic has been updated by aleex (previous revision, new revision, compare).

I did the Div2 B question using STL map in C++ , but got a runtime error in the last system test . I was erasing the keys having 0 value . I resubmitted it after removing the part where I am erasing from the STL map and it got accepted . This has happened before also when I was trying to erase from a STL set. Can anyone elaborate why runtime error occurs in such cases !!

Submission with runtime error : 50026129

Submission with AC : 50037712

50009667

O(n) solution for div1B without string algorithms. (Ignore everything before function go(l, r))

Nevermind, didn't notice author's solution for bonus problem.

Div 1B: Bonus task is to solve this in linear time, but does not author's solution work in worst case O(n log n)?

What's the proof that ans of div2D can be atmost 2 ?

I wonder how we can solve Problem C from Div.1 using segment tree in O(log(q)) per query. I came up with nearly the same solution, but what I have in mind for the type-3 query is to binary search the earliest time that the time get under 0, which will cost O(log(n)²). Can someone tell me if there is a better way to do this?

For 1113A — Sasha and His Trip

We can also solve it in less complexity O(1) without using any loop

Solution:

int n,v,ans;
cin>>n>>v;
if((n-1)<=v){
    cout<<n-1<<endl;
} else{
    ans=((n-v)*(n-v)+(n+v))/2-1;
    cout<<ans<<endl;
}

In problem 1D, why we can just multiply f(n,edges+1)? Why it calculates all the cases? And I think that in each tree of these forests， we choose a vertex with the minimum index as a root, and connect edges+1 roots to a path from a to b. Is my understanding right?

can anyone please explain why in Div2 problem C the "cnt[1][0] = 1;" is set to 1? I'm not able to get the logic here

In the Question: Sasha and a Bit of relax, in the Author's code, what is the use of cnt[1][0] = 1. Can anyone explain

For Div2 C what is L and R. Are they index of arrays or values between which we have to apply xor operation?

How can L and R be the indices of array in DIV2 C? How can 6 be index of array of 6 elements ?I am unable to find what are L and R.

Very nice to see a contest on the weekend : ), i hope there will be much more. Thank you.

I think I have a better solution for problem B (or main-tests are weak!) I guess that for every member of array (a[i]), the divisor of it that lead us to minimum (so we divide a[i] on it and multiply our minimum member of array to it) is the divisor that is nearest to square root of a[i]. so we can first sort the array, and then for every member of the array iterate back from sqrt(a[i]) to 1 and when we see a divisor of a[i] calculate the Delta that choosing it gives us. But I couldn't prove my conjecture. Anybody can help? I think the order will be O(n.sqrt(a[i])). Sorry for bad English.

Am I the only one who wonders how could several people solve Div. 2 C / Div. 1 A in only 2 minutes? Really, there is quite a bit of thinking and coding in this problem. And also, IMHO Div. 2 D is easier than Div. 2 C, I solved them for 10 and 30 minutes correspondingly.

why we initialize the array that count 0 for odd positions with 1? i mean why in the author's solution cnt[1][0]=1 ?

Proof / explanation of Div 1 B bonus solution in O(n)? Thanks for any help!

I think C is TooDificult

Well...I think the "forsests" in the tutorial of 1D should be replaced by "forests".aleex

On Div2D / Div1B, an interesting theorem is that odd-length palindromes can never be rearranged into a different palindrome with only one cut. Bonus: Prove it :)

For example, this gets AC: http://codeforces.me/contest/1113/submission/50039408.

Thank you very much for this editorial! But, as I suspected, problem F was really too straightforward and boring. I came up with a simple greedy solution during first 10 minutes of contest, but sadly I couldn't solve it because I am still div2 and didn't participate.

Finally done with proof and implementation of Shasha and Interesting Fact from Graph Theory(div2. F) question. One thing I am missing with the editorial is that why we have to first choose vertices on fixed path and then rerrange them? Shouldn't it be just picking up edges -1 vertices from n-2 available, and not rearranging them — (because as per question, "2 trees are distinct if there is an edge that occurs in one of them and doesn't occur in the other one. Edge's weight matters.")

Div2D/Div1B can be easily solved in O(N), where N is the string length.

First, consider the cases where it is impossible. It is impossible iff: N is even and all the characters are the same, or N is odd and all characters but the center one are the same. In these cases, there is only one possible palindrome that can be formed anyway.

We show that ALL other palindromes can otherwise be solved in 2 cuts. There exists an i such that the prefix of i characters is different from the suffix of i characters. Cut off the prefix and suffix and notice that the remaining string is still a palindrome. Simply switch the places of the prefix and suffix and we get a different palindrome from what we started with. We know that i exists, because otherwise it would reduce to the impossible case.

Now, we identify the palindromes that can be done in 1 cut. I will use B to denote some string, then B' to denote its reverse. Notice that if B ≠ B', then B'B and BB' are distinct palindromes. Similarly, if we have BB'BB', we can use 1 cut to slice off the last B' and then place it at the beginning, which gives us B'BB'B, a different palindrome. If a string can be decomposed as a series of BB'BB'... BB', with B ≠ B', then it can be solved in 1 cut. A string canNOT be decomposed in such a matter if its length is odd; then, there would be some central pivot.

We thus implement a recursive function. If N is odd, then it definitely cannot be solved in one cut. If N is even, we check if the left half equals the right half. If they are not equal, we return true. If they are, we recurse on one of the halves to see if that can be decomposed (and since the two halves are equal, if one of them can, the other can too).

bool in_one(int n)
{
	if(n&1)
		return false;
	string a = s.substr(0,n/2);
	string b = s.substr(n/2,n/2);
	if(a==b)
		return in_one(n/2);
	else
		return true;
}

Naive string comparison of the left and right half is O(N), so the total work done is at most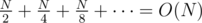 . This can be reduced to by using hashing for string comparison, but reading the input is O(N) anyway.

To summarize, check if this palindrome is solvable. If it is, check if it can be done in 1 cut. If it cannot, then it can be done in 2 cuts.

wtfrick this is

Is it possible to do Div2B if you are allowed to execute the operation as many times as you want?

In problem div1A we can say that if we divide the segment into two groups made up of any element and of any size will have same xor value.

D1F can also be solved using DnC and rollbackable DSU in $$$O(n \cdot m \cdot log^2{(n\cdot m)})$$$.

Implementation: link